Robust Virtual Network Embedding Based on Component Connectivity in Large-Scale Network

Xiaojuan Wang, Mei Song＊, Deyu Yuan, Xiangru Liu Beijing University of Posts and Telecommunications, Beijing 00876, China

2 People’s Public Security University of China, Beijing, China

* The corresponding author, email: songm@bupt.edu.cn

I. INTRODUCTION

Software-Defined Network (SDN) [1] as a hot topic in recent years is a very promising way to address the network ossification problem.SDN [2][3] as an enabling technology for network virtualization has enabled innovation in traditional network. The implementation of network virtualization in SDN was introduced in [4], [5]. SDN decouples data plane and control plane, and simplifies network management. Multiple virtual network (VN) requests can share the same physical nodes and links through the “slices” allocated by SDN controller. So after SDN [6] is implemented, the virtual network embedding (VNE) [7][8] problem should be considered as a key issue in order to achieve flexible and automatic management of the substrate network (SN) resources.

VNE problem is mainly concerned with mapping virtual network requests onto a shared substrate network reasonably and efficiently. In such circumstance, the problem is NP-hard [9][10] even if all VN requests are known in advance. In order to reduce the hardness of the VN assignment problem, research has been restricting the problem space in different dimensions. For example, [11], [27]consider offline version of problem (i.e., all the VN requests are known in advance),[13]adopted a Column Generation (CG) formulation of the VNE problem, [12] ignores either node requirements or link requirement and[11]- [14] assume infinite capacity of the substrate nodes and links to obviate admission control, [15][16][18] only think about some special topologies of virtual network like star,tree and ring topology, [25] considers that the VN requests are dynamic and designs online and offline algorithms to process the VN requests, [26] proposed heuristic algorithm based on Ant Colony Optimization and genetic algorithm which aims to decrease the computational complexity.

However, most of recent researches focus on how to reduce the hardness of the NP-hard problem such as [1], [14], [15]. They thought more about the connectivity of local nodes and embed the nodes with greedy methods. As for link embedding, many solutions [19] have been proposed such as shortest path, k-shortest paths (ksp), multi-commodity flow algorithms[7] and load balancing [17]. These algorithms can efficiently reduce the hardness of the NP-hard problem. However, preselecting node mapping stage without considering its relation to the link mapping stage restricts the solution space, and may result in poor performance in large-scale network. So how to embed VN request onto large-scale [22]-[24] substrate network is presented in this paper.

We present a robust VNE algorithm based on one-shot k-core VN embedding which takes the global connectivity of the residual substrate network into consideration. As we know, the residual substrate network will be decomposed into multiple components with accepting VN requests in large-scale network which due to the depletion of link resources.Moreover, the network failures are common in IP-backbone network which aggravates the network fragmentation. So it is of utmost importance to consider component connectivity in large-scale network. In our algorithm,we embed the VN request onto one specific components using k-core theory [21] which is always applied in large-scale network. The primary thing is to distinguish the different components and select appropriate ones as candidates for VNE. At this stage, the load balancing is considered which can be used to avoid blocked or bottlenecked area of substrate network. In this way, robustness can be guaranteed that in the event of nodes and links failures in substrate network fewer VN requests will be influenced. At last, we embed each node and link according to the hops between two substrate nodes. Thus reduction of the cost of every VN request can be achieved.

The rest of the paper is organized as follows. In section 2, we propose a detailed description of the problem and network model.Four performance metrics are also introduced in this section. In section 3, we discuss the details of the component connectivity in largescale network. And we analyse the existence of giant component. In section 4, we discuss the details of the k-core theory and present a new robust VNE algorithm based on component connectivity in large-scale network.And a formalized description of the algorithm is presented. Section 5 shows the results and analysis of the simulation of four VNE algorithms. Finally, section 6 concludes our work and identifies future research directions.

In this paper, the authors propose a robust VNE Algorithm based on component connectivity in largescale network which diあers from the previous algorithms.

II. FORMULATION AND EVALUATION METRICS OF VIRTUAL NETWORK EMBEDDING

2.1 Formulation of VNE algorithm

Definition 2: Virtual network request. We model the virtual network request also as a weighted undirected graph GV=(NV,LV),where NVrepresents the set of VN nodes and LVrepresents the set of VN links. Each VN node nV∈ΝVis associated with a weight cpu(nV) which denotes the capacity requirement of computing resources at virtual node nV. Each virtual linkrepresents that the link is between virtual nodesand it has a bandwidth capacity requirement bw(lV).

Definition 3: Residual substrate network.Residual substrate network is defined aswhere NRand LRdenote the set of the residual nodes and links respectively.

VN embedding is a NP-hard problem. Most of recent researches focus on how to reduce the hardness of the NP-hard problem. The embedding of VN requests is separated into nodes embedding and links embedding. At node embedding stage, we calculate available resource (AR) of each substrate node as following:

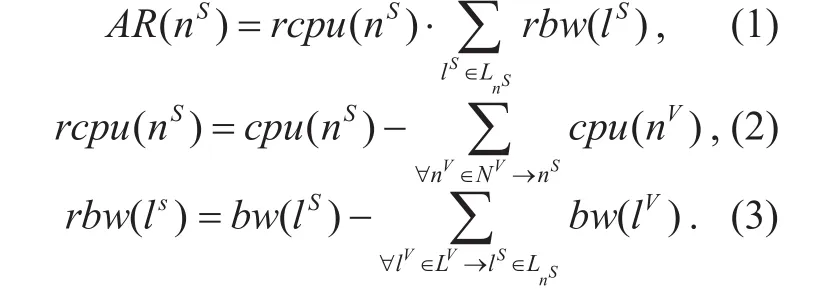
Where LnSrepresents a set of links which are connected to node nS. Meanwhile, rcpu(ns)and rbw(ns) represent the residual resources respectively. As for VN request, there is a similar formula with formula (1) while we don’t need to calculate the residual resources of lVand nV. Then we sort AR in descending order and embed virtual nodes onto substrate nodes with maximum residual substrate resources according to that order. At the link embedding stage, k-shortest paths algorithm is used to find the shortest path between two embedded substrate nodes.

2.2 Virtual network embedding performance metrics

When the VN request comes, outcome of VNE algorithm will give a response of accepting it or not. If the VN request is accepted,the substrate network will allocate underlying resources to VN. After embedding the virtual network, there are several metrics to evaluate the performance of embedding algorithm.

(1) Acceptance ratio. The acceptance ratio of virtual network requests is defined as the ratio of the accepted virtual networks to all the arrived virtual networks. It is one of the most important performance metrics to evaluate virtual network embedding algorithm. It is defined as:

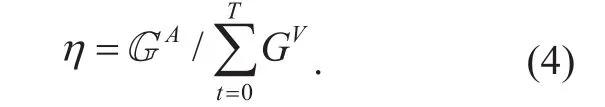
Where GArepresents the number of accepted virtual network requests and T represents the total running time of the VNE algorithm.The acceptance ratio is influenced by the embedding algorithm, the arrival rate and the duration of the virtual network, the substrate network and some other reasons. So when we make the simulation, environment must be the same except for the embedding algorithm.

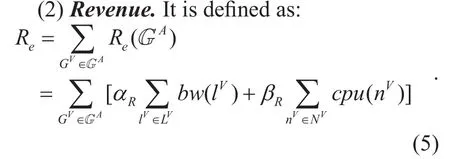
Where αRand βRare adjustment parameters which are used to balance the weight of the cpu and the bandwidth of the virtual network.Revenue is one of the most important evaluation criteria. It shows the economic benefits received by the virtual network request for the substrate network operators.

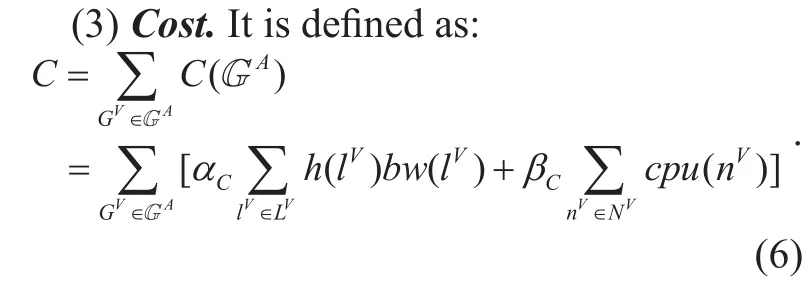
Where hl()Vequals the number of substrate links which are deployed to embed virtual link lV. αCand βCare adjustment parameters which are used to balance the weight of the cpu and the bandwidth in the substrate network.CG()Vshows how many resources will be taken when one VN request is embedded onto SN.

(4) Robustness. It shows the ability of virtual network to work properly when the substrate failure occurs. In this paper, we use Rnto show the robustness of the virtual network.Rnis a probability that the virtual network can still be able to work properly in the event of link failures which shows the robustness of the VNE algorithm. Roexpresses the network vulnerability and can be formulated as the ratio of virtual links which are affected by substrate link failures and the total virtual links, thus Rnis defined as 1- Ro.

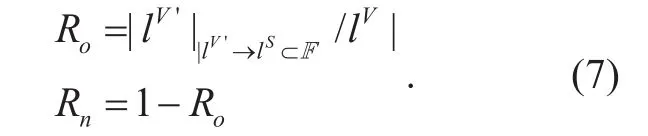
Where F is a set of failure substrate links and lV'is a set of affected links.

III. COMPONENT CONNECTIVITY ANALYSIS IN LARGE-SCALE NETWORK

3.1 Component connectivity theory

When the network scale is relatively large,switches, routers, mobile bases and other nodes have connection preference, that is, the nodes have the characteristics of heterogeneity and the connection probability between two nodes is p. The degree distribution of the node follows the power law distribution, and the distribution function is as follows:

Where αkis scale-free constant, k is the number of adjacent nodes. Through formula (9),we can see the power law distribution has the invariance of scale.

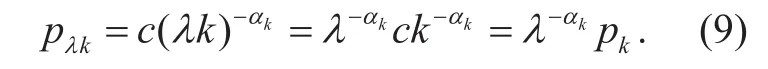
Component connectivity is important in large-scale network. In the following part, we introduce two measurements which are giant component and small components.

(1) Giant component. In network evolution,if the scale of a component is proportional to the number of node, it is regarded as giant component S. In virtual network embedding progress, giant branch can be approximately considered as the largest connected component of the network. With the increase of accepting VN requests, the scale of it may decline. However, in a certain threshold range of blocked links and failed nodes, giant component always exits.

(2) Small components. It is defined as remaining network components after removing the giant component. There is at least one path between any two nodes in a small component.The scale of small components measures the degree of fragmentation of the network. It is efficient to choose a connected component to embed VN request to prevent that virtual nodes embedded in two components can’t find a path due to the dis-connectivity. If we choose the giant component to embed VN, the probability of success is the greatest. However, it is unwise to always choose the giant component, we should take load balance and topological characteristics of both component and VN into consideration. Topology identification and load balance are applied in the VNE algorithm which will be explained totally in the next section.

As we can see in figure 1, the substrate network is divided into a few components including one giant component and a few small components because of the block of substrate links. The component consisting of green nodes is giant components and the others are small components whose scale are smaller.

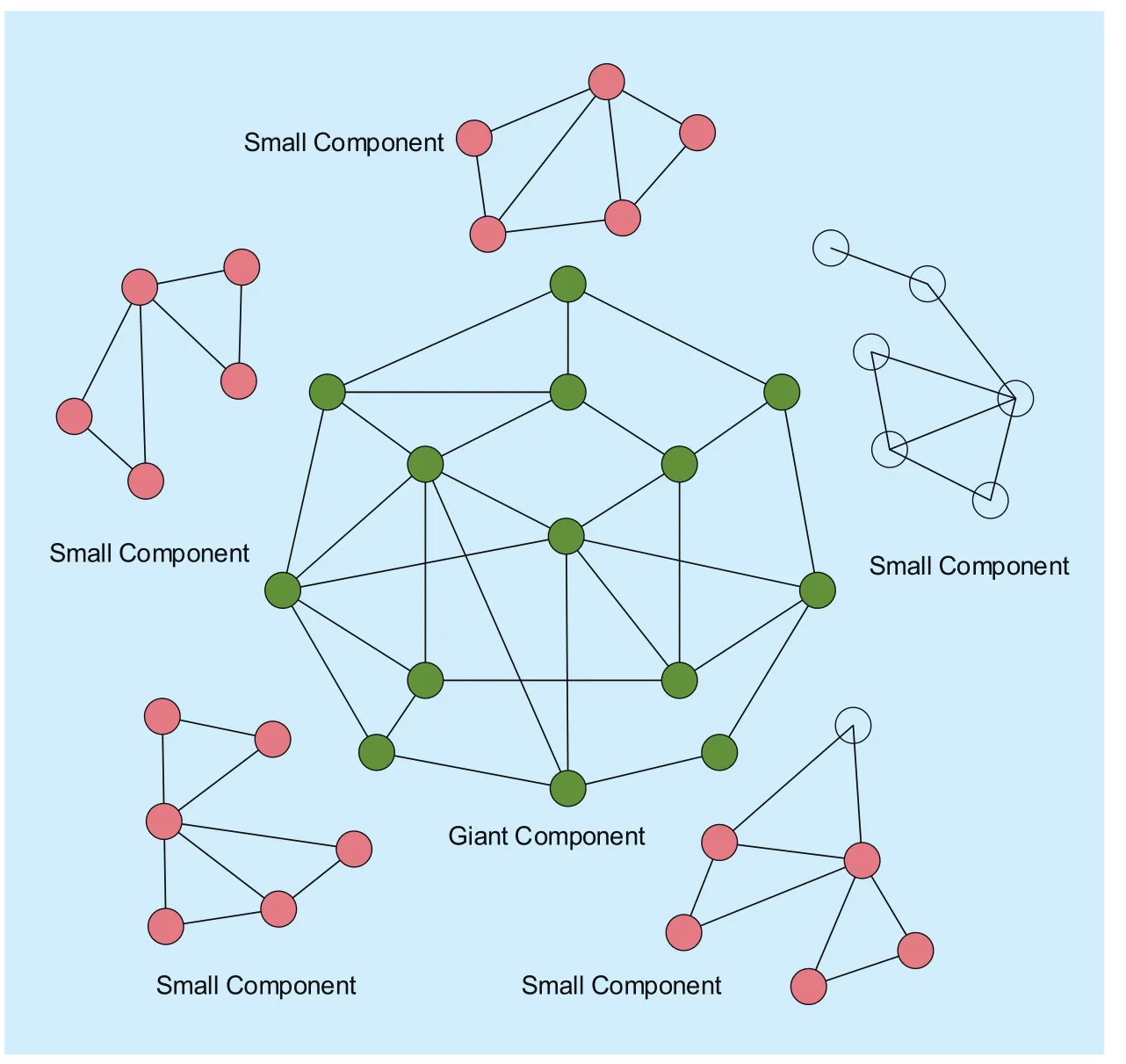
Fig. 1 The example of giant component and small component

Component connectivity is statistic characteristic, this section is the theoretical analysis of the network performance at node failure situation. The functions shown in table 1 are the generating functions used in the analysis.

The degree distribution and the redundancy distribution are not independent of each other,which can be transformed into each other.

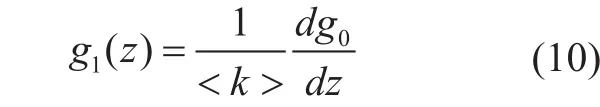
Where is the average value of the degree.

3.2 Component connectivity theory

Assuming that ρsrepresents the probability of one node belonging to a small component whose size is S after removing an adjacent node of the node. Psk(1|)− represents that when node i is removed the size of the sum ofthese small components which contain its k adjacent nodes respectively is s. So the probability πsof node i belonging to small component whose size is s is equal to the average value of Psk(1|)− which is :

Table I Generating function

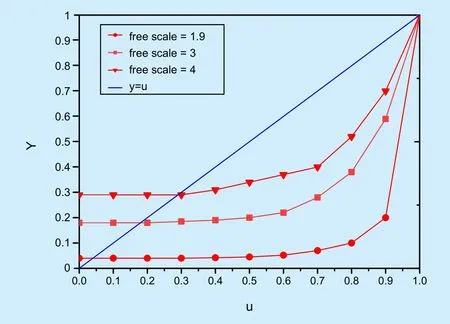
Fig. 2 The equation solving in scale-free network

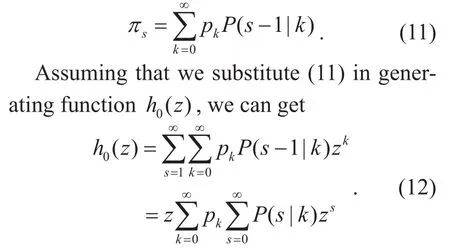
Because the scale of the small components is independent of each other, we can get formula (13) by using the free-scale property of the generating function

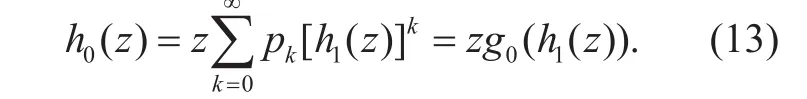
In large-scale network, the degree distribution will correspond to the redundancy distribution qkwhen node i is removed, so

As shown in figure 2, using graphic method to solve equation (17), we can see with growing, increasing speed of g1(u ) is becoming more and more slowly and the intersection of the two curves will shift to the right.

3.3 Robust analysis based on giant component

As shown in equation (18), we let φ be the retention probability so that 1−φ is the failure rate. We define u as the probability that node can be not connected to the giant component.So the probability that node is connected to giant component without its own links is uk.According to degree distribution function,the probability of node not belonging to giant component isg0(u ). According to the research, there are two conditions that node i is not connected to giant component. First,failure causes the node to disconnect from the giant component; second, the node does not belong to the giant component at the beginning. So the probability that the node does not belong to the giant component is as follows:

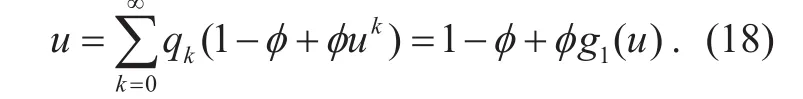
When u=1, the equation is established, that is, nontrivial solutions exist. To solve the giant component, we need to find out the nontrivial solution. The condition of the equation having solution is the two curves are tangency, that is

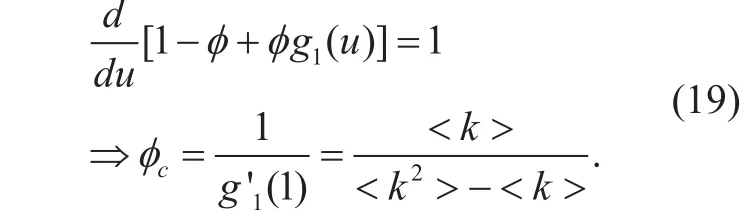
In order to find out the scale of the giant component, we deploy generating function g1(u ) at u=1.

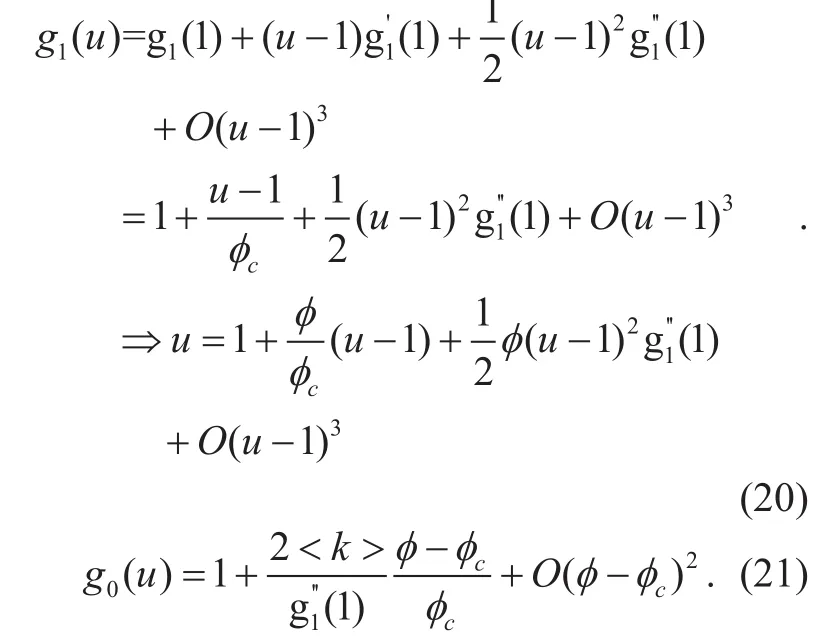
We substitute (20) and (21) in (10) to get the solution.

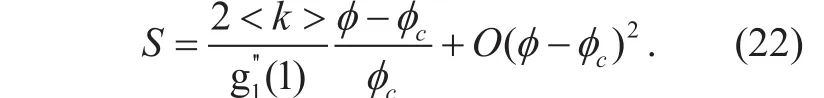
According to the result, if φ approaches to φc, the correlation of the giant component and the threshold is linear. The arrivals of VN requests are modelled by a Poisson process and the node failures are modelled by a random distribution. The process of VN embedding is similar to the process of giant component disappearing and small components increasing.

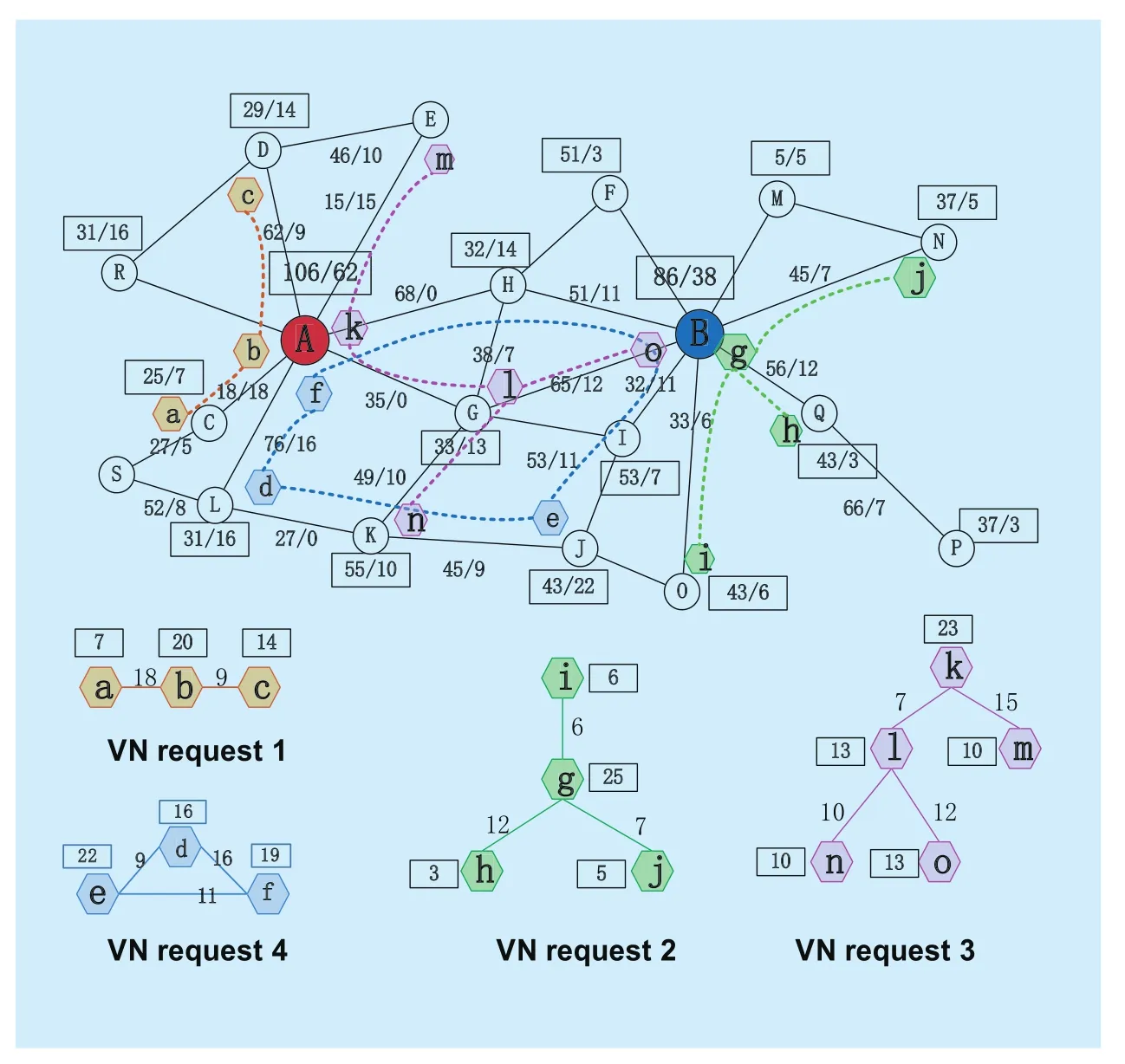
Fig. 3 Process of the VN embedding

3.4 Association analysis with vn embedding

In complex network, with the increase of accepting virtual network requests, the topology of available residual substrate network will be changed. The performance metrics are relevant to the connectivity of residual network.

Figure 3 is a part of the substrate network.There are two numbers in the rectangle (over the links) of SN, the former represents substrate node’s cpu (bandwidth of substrate link), and the latter is the residual resource of substrate cpu of node (bandwidth of substrate link). The number in the rectangle of VN request represents the virtual nodes cpu, the number over the virtual links represents the bandwidth. As shown in figure 3, the resources of substrate links L-K, A-G, A-H have been exhausted which means the residual network is decomposed into two components, component A and component B. The component with the most substrate nodes is considered as giant component such as component B (the right part of figure 3) and the others are considered as small components.

When using traditional two-stage algorithm to embed VN request 1 onto the substrate network, there will be two steps including node embedding and link embedding. In the node embedding phase, substrate nodes with the most resources will be selected as the candidates to embed virtual nodes of VN request 1 such as A, B and G. After the node embedding phase, the link mapping will be triggered, but unfortunately, there is no path between node A and node B because A and B are in two different disconnected components. As a result, the mapping will fail.

In our algorithm, firstly, we select one suitable component using our component discovery algorithm. The substrate network in figure 2 has two components, component A and component B, component A is selected according to our algorithm because it’s scale is big enough to embed VN and its resource utility is lower. Secondly, we choose a corenode of component A to embed the core node of VN 1. Core node has the attributes of best connectivity and sufficient resources. After the evaluation, node A was selected to embed virtual node b. At last, we embed the VN request on the selected component using the one-shot algorithm based on k-core theory which is explained totally in the following section. After the embedding, virtual node a, b and c are embedded onto the substrate node of C, A and D separately.

Table II Process of VN embedding

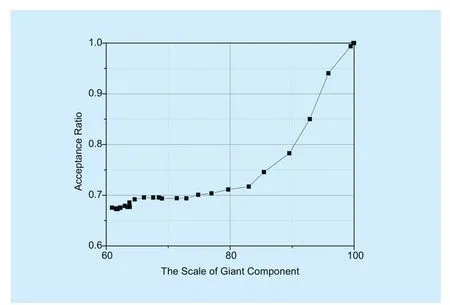
Fig. 4 Relationship between acceptance ratio and the scale of giant component

The process of the algorithm is showed in table 2 and the details of its implementation is totally explained in the next section.

As shown in figure 4, it has a relationship between acceptance ratio and the scale of giant component using two-stage algorithm. And other algorithms have similar characteristic. At initial phase of the mapping (the scale which equals 100 is the beginning) the scale of giant component is larger and the correlation of the giant component and acceptance ratio is obviously linear. With the decrease of the scale of giant component, acceptance ratio will tend to be stable. The algorithm in this paper try to keep the giant component large. In this way,more VN requests can be embedded successfully.

IV. ROBUST ALGORITHM DESIGN BASED ON COMPONENT CONNECTIVITY

With the arrivals of VN requests, the topology of residual network will be changed. And there will be a giant component and several small components in residual network. In order to find out the component that can be used to embed an arriving VN request, we have to take account of the number of nodes and their connectivity. So we divide the nodes and links of the component into several shells according to the connectivity. And k-core theory is always applied in complex network to divide nodes based on their connectivity.

4.1 Component discovery

With the increase of accepting VN requests, a lot of substrate links have been depleted or the remaining resources of them are too little to accept virtual links. Links like that are considered as disconnected, so that the topology of residual network will be changed. And there will be a giant component and several small components in residual network. In order to find out the component that can be used to embed an arriving VN request, we have to take account of the number of nodes and their connectivity. So k-core theory is applied to divide the nodes and links of the component into several shells according to the connectivity which is always used in complex network to analyse the connectivity of the network.

The k-core theory is always used in complex network. In graph theory, the maximum sub-graph whose node connectivity is at least k is called k-core. If we remove all the k-core nodes from (k-1)-core node set, we can get a sub-graph which is called k-shell in this paper.The way to get k-shell is like peeling onions:remove every node whose connectivity is 1 till the sub-graph does not contain 1-connectivity degree nodes. The removed nodes set is called 1-shell. The more shells a component has, the better its connectivity is. VN and components of SN can be processed in the same way. In our algorithm, if the number of the shells of component is larger than that of VN by ε, we assume that the component is large enough to embed the VN.

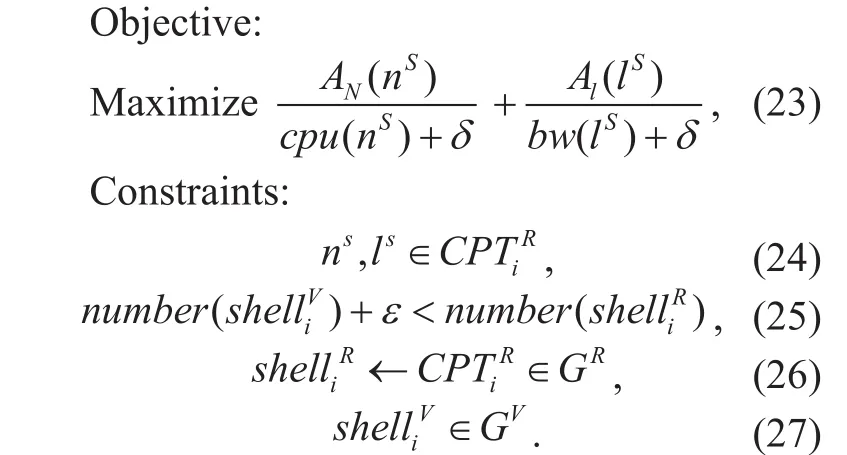
Where GRis a set of components of the residual network,is one of components and number(shelli) is the number of shells of CPTiand ε is a parameter that guarantees the component selected larger than VN. When the size of the component meets the requirements,the objective function (23) prefer to choose that with the latest resource utilization. If the objective function has no solution, then select the component with the maximum number of shells as the candidate to embed VN.

4.2 Evaluation of core node

A pretty important thing of the algorithm in this paper is to find out the core node of each VN request and embed it onto the corresponding substrate node of the selected component.Core node has the attributes of best connectivity and suffi cient resources. Firstly, we should transform the virtual topology to several shells represented by (where k represents connectivity of k-shell) and the innermost shell always contains several nodes. In order to take both the cpu and bandwidth resources into account,we choose the node which has the maximum AR as the core node from the innermost shell and AR is calculated by formula (1).

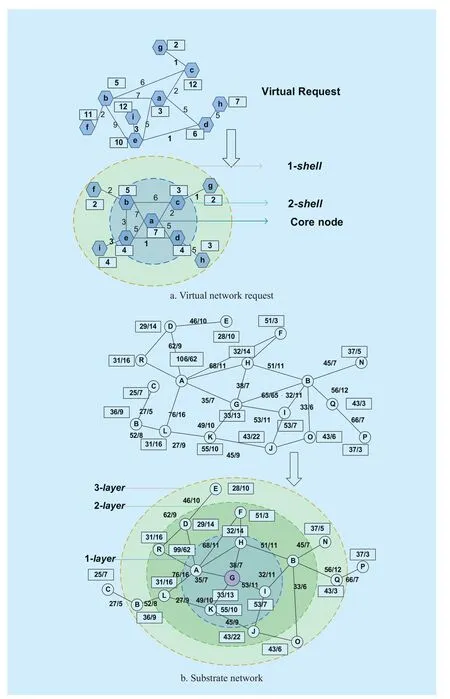
Fig. 5 Robust VNE algorithm based on k-core

As shown in figure 5, we divide the links and nodes of the VN request into two shells through k-core theory. The represents 1-shell containing nodes f, g, h, i and therepresents 2-shell (also called 2-core) containing nodes a, b, c, d, e. And node a is the core node of the whole VN topology.

Next we could search the selected component as shown in (b) to find a similar topology to embed the VN.

In order to embed VN request into component (b), we choose a substrate node to embed the core node of VN request by load balancing. When the resources are satisfied, we select the substrate node with lower resource utilization rate. Load balancing will improve the connectivity of the residual SN and survivability of VN. And the cost of each VN will decline.

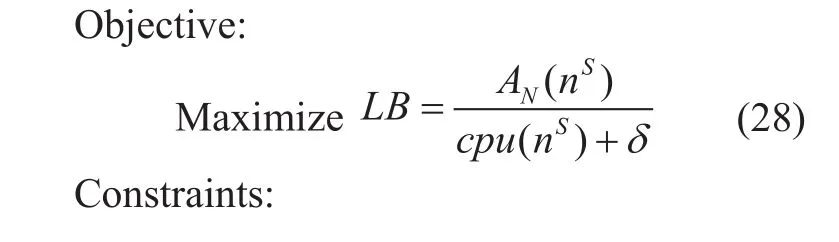
Table III Function of change_VN

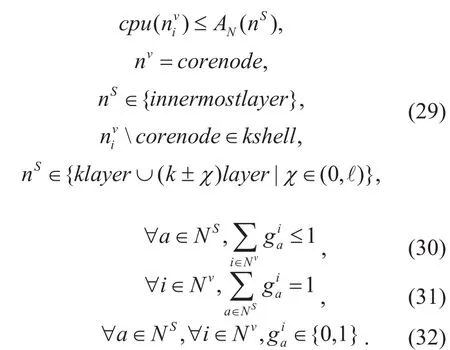
Where AN(nS) is residual cpu resource of node nS, δ is a constant approximately to zero,cpu(nS) represents the initial cpu resource of node nS. Constraint (29) makes sure that substrate cpu is enough for virtual node and the ℓ is a parameter to control the range of the underlying nodes that virtual node belonging to k-shell can embed on. Constraint (30)makes sure that only one substrate node is selected for each virtual node which is from the same VN request. Constraint (31) represents that one virtual node which is from the same VN request can be embedded onto only one substrate node. Constraint (32) shows thatis binary constraint. In this way, we can find the minimal LB substrate node which is called substrate core node (SCN) to embed the core node of the VN. This will ensure load balancing.

Table 3 shows the process of partitioning VN into shells and finding out the core node.

4.3 Shell embedding

Being different from two stages VNE algorithm, our algorithm is one stage which means that the embedding of virtual nodes and links is simultaneous. We present the shell embedding formulation in the following manner.

Objective:

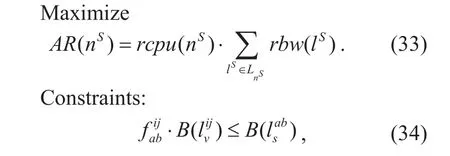
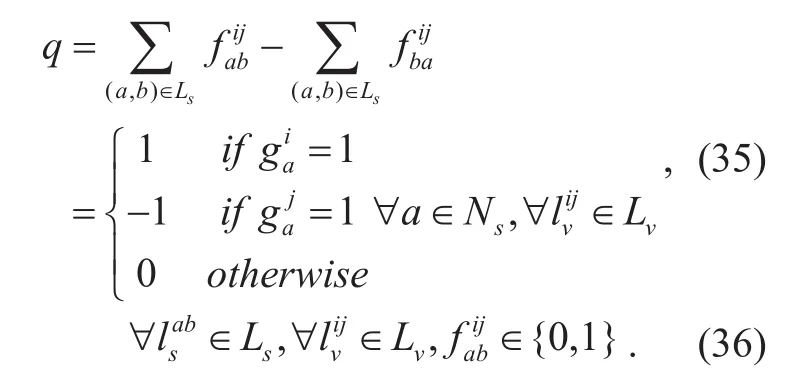
Objective (33) is the same as (1). And the constraints include (34) - (36) as well as (29) -(32). Constraints (34) represents that substrate bandwidth must be sufficient for the virtual link lv

ijwhere ijN∈vand node j has been embedded. Constraint (36) represents that virtual link lv

ijis embedded onto substrate link ls

ij. Constraint (36) is binary constraint.

In 4.2, we’ve found out the core node and embed it onto the corresponding substrate node belonging to the innermost layer of the selected component. In order to simplify the computational complexity of the Mixed Integer Linear problem above, an improved VNE algorithm has been showed below. We embed the virtual shells from inside to outside. As shown in figure 5, we divide nodes into different layers by the number of hops to SCN. The innermost shell will be embedded onto 1-layer. And k-shell will be embedded onto k-layer first, in the event of embedding failure, start the iterative process. A parameter ℓ is applied to control the number of iterations. The detail how we embed the shell is shown in the following table.

As shown in table 4, the main procedure begins with getting state of Substrate Network and. Next we embed the core node onto SCN by load balancing. Then we need to embed the rest nodes and links of the VN request. First we embed each shell successively. And for each shell, we must find a corresponding layer in SN. For example, the SN layer corresponding to the innermost shell is 1-layer whose nodes is one hop to SCN. Next we research all of the nodes in 1-layer in order to embed the nodes and links in innermost shell. If there were virtual nodes in innermost shell can’t been embedded onto 1-layer, we must find the 2-layer embed the rest nodes. Iteration can be several times. In our simulation, the number of iteration is two.

V. SIMULATION RESULTS AND ANALYSIS

5.1 Simulation environment

We did three sets of simulation. For the first set of simulation, the VNE algorithm is the same and variable is the number of virtual nodes which are 7, 10 and 15 respectively. As for the second set of simulation, the number of substrate network and the arrival rate of the VNs are variables. In the last set of simulation, the number of virtual nodes is randomly determined by a uniform distribution between 5 and 15, and each pair of virtual nodes is randomly connected with probability 0.3. The computing requirements (cpu) on VN nodes follow a uniform distribution from 1 to 5, as well as the bandwidth on VN links from 20 to 30. The arrivals of VN requests are modelled by a Poisson process (with mean of 10 requests per 100 time units). The duration of the requests follows an exponential distribution with 4000 time units on average. The SN topology used is generated with 100 nodes usingthe GT-ITM tool. The computing (bandwidth)resources of the substrate nodes (links) are real numbers uniformly distributed between 50 and 100 (200 and 300). And each pair of substrate nodes is randomly connected with probability 0.15.

Table IV Improved VNE algorithm

To simplify the virtual mapping, αRand βRare both set to be 0.5. We embed the VN requests one by one as [25].

5.2 Comparison method

In our evaluation, we have six algorithms that combine different node embedding and link embedding strategies including our contributions and algorithms from previous research[1][8] modified to fit into our model. The notations that we use to refer to different algorithms are enumerated in table 5.

5.3 Simulation results and analysis

In our evaluation, we measure the average η,Re, C, Roand several other performance metrics for VN requests over time. In all these cases we plot the performance metrics against time to show how each of these algorithms(table 4) actually perform in the long run. We summarize our key observations in the following. In this paper, we call the number of virtual nodes are 7, 10, 15 as N7, N10, N15respectively.

As shown in figure 6, with the number of virtual nodes increase the acceptance ratio declines, the average cost ascends. Because the size of VN request is larger, it will take up more resources. The revenues of N7are less than N10, N15. Because in the duration of N7,SN resources are not exhausted. With time goes by, the revenue of N10 and N15tends tobe equal. However, the cost of N15is more than N10. Because the virtual nodes will be embedded onto two farther substrate nodes with the increasing of virtual nodes which will consume more substrate resource.

Table V Compared algorithm

As shown in figure 7-a, with the increment of scale of the substrate network, the acceptance ratio of the VNs has also increased and eventually has approached to 1. Four curves in Figure are different from the arrival rate and the life time, which is on behalf of the pressure of the substrate network. It can be concluded that more arrivals of VN per 100 time units and longer its life time mean the acceptance ratio will be lower. Because the resources of the substrate network are limited. When the scale of the substrate network becomes larger which results in adequate resources, the acceptance ratio also starts to increase and eventually becomes 1. The algorithm we proposed precisely shows the law of the change and is still applicable well when the network is large.

The x-axis in figure 7(b) represents the number of VNs that arrives in 100 time units,the larger the value, the more resource pressure is imposed on the substrate network. The four curves show the variation of the acceptance rate with the arrival rate of VN under different substrate network scale. In the same substrate network, when VN arrives more,the acceptance rate becomes correspondingly lower. When the number of VN arriving is very large, the acceptance ratio becomes very low. In our simulation which compares our algorithm with others, we chose the appropriate arrival rate to show the relationship between them better as shown in figure 8.

Figure 8 shows the performance metrics η,Re, C, Rounder different algorithms. We can get the following conclusions.

(1) As shown in figure 8(a), the acceptance ratio of four algorithms during the simulation.As we can see, acceptance ratio drops quickly after 1600 time units because there are sufficient substrate resources for the arrived VN requests before 1600 time units, and when the amount of running VN requests in system are stable (after 5000 time units), acceptance ratio would keep consistent. The acceptance ratio of our algorithm is higher than the other three algorithms. In complex network situation, LBPS algorithm has a higher acceptance ratio than KSP and PS algorithm, because they may make some substrate paths more blocked and it is harder to find available paths for virtual links. And as time goes by, PS algorithm makes the substrate resource more fragmented and the SN connectivity decline so it has the lowest acceptance ratio. The algorithm we proposed achieves almost 20 percent improvement of acceptance ratio in the long run. This is because the algorithm we proposed takes the connectivity of the residual substrate network and the resource balance into consideration.Embedding VN requests onto one connected component will improve the probability of acceptance and the load balance can prevent the substrate links from blocked. Besides, our algorithm is one shot and is based on k-shell theory which embed the VN request onto several shells. Its mapping range is more concentrated and is easier to be accepted.

(2) As shown in figure 8(b), before 1600 time units the revenue of the four algorithms is the same. Because there is enough resource for the VN requests at the beginning. As time goes by, the revenue of LB-PS and KSP is becoming stable. But the revenue of PS has an obvious declining trend and then tends to be stable. Maybe because PS algorithm makes the substrate resource more fragmented and the SN connectivity decline. Compared with the other three algorithms, the algorithm in this paper has an obvious advantage in the average revenue. Because the large-scale SN can accept more VN requests by robust VNE Algorithm based on k-core.

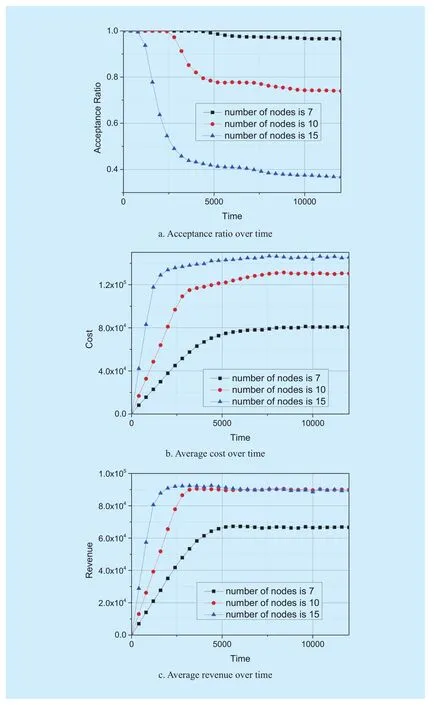
Fig. 6 Performance metrics under different virtual nodes

(3) As shown in figure 8(c), at the beginning, the average cost of K-core is lower than the other three algorithms. In relation to figure 8-a we can see that our algorithm needs less substrate resource for the same VN request.Because our algorithm makes the virtual nodes be embedded onto closer substrate nodes. After about 2500 time units, the average cost of k-core is equal to KSP. But it has a higher acceptance ratio. The complex VN contains more nodes and links which makes the residual SN connectivity decline. When the VN request becomes more complex, the algorithm in this paper has an obvious advantage. According to figure 8(c), with regular VN arriving and leaving, embedding cost of k-core VNE algorithm has more than 10 percent saving over LB-PS which means there are more residual substrate resource can be used. So there are some places can be improved in our algorithm.

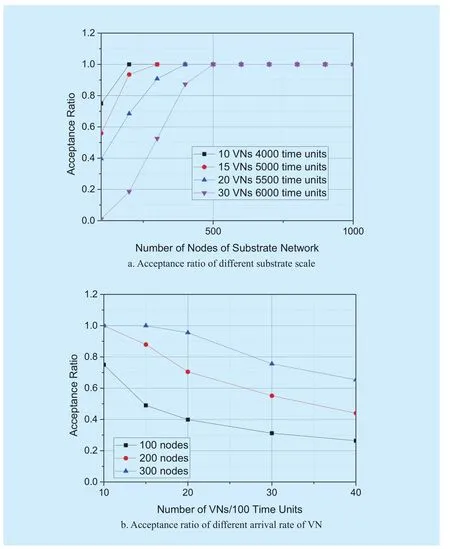
Fig. 7 Acceptance Ratio under different scale of substrate network and arrivals of VN

(4) As shown in figure 8-d, LB-PS, KSP,PS, NLB-PS, Node&Link-LB have similar curves of Ro. Because all of the five algorithms are two-stage algorithms, the differences are in link embedding stage. However,the algorithm in this paper is a one-stage VNE algorithm. We use component discovery algorithm and k-core theory based embedding algorithm. The component VN embedded on is more connected and one virtual link has embedded on fewer substrate links because the algorithm we use prefers to select nodes on adjacent shells. So in the event of substrate link failure, the virtual links with fewer hops is less affected and is more robust.

Figure 9 shows the scale of giant component and the number of small components over time. We can get the following conclusions.

(1) As shown in figure 9(a), the scale of giant component equals 100 before 1600 time units but drops quickly after 1600 time units because there are suffi cient substrate resources for the arrived VN requests, and when the amount of running VN requests in system are stable (after 5000 time units), the scale of giant component would keep consistent. The algorithm presented in this paper has the best performance. Combined with figure 6, we can see the results conform to the theory proposed in section 3 that is the scale of giant component is larger, the VN request is more easily to be embedded. However, PS is a little different from other three algorithms. There is a trough in PS curve. Because PS algorithm makes the substrate resource more fragmented and the connectivity of residual network declines.In the PS curve, we can see obvious ups and downs, this is because PS algorithm is easy to make the residual substrate network fragmented. When the substrate network is too fragmented to accept a VN request, its acceptance ratio is low until some embedded VN leave the substrate network and release the substrate resources. When it begins to accept VN, the SN becomes fragmented again. Compare to figure 6-a, it can be seen acceptance drops quickly before 6000 time units and becomes stable after that. And in this figure, giant component drops quicks around 6000 time units.After 6000 time units, the curve starts to rise because of the embedded VN leaves and low acceptance ratio.

(2) As shown in figure 9(b), the number of small components is 0 before 1600 time units but it rises quickly after 1600 time units. And it keeps stable after 5000 time units. However,PS is a little different from other three algorithms. There is a peak in PS curve and it has the fewest small components among the four algorithms. As shown in figure 8-a, because PS algorithm makes the substrate resource more fragmented and the connectivity of residual network declines and there are fewer VN requests can be embedded onto SN.

As shown in figure 10, we create an ex-treme BA network which includes several components in order to explain the relationship between components and VNE. Compared with figure 8-a, there is a clear decline in curve of KSP and the acceptance ratio of LB-PS and PS decline too. The result shows that the algorithm in this paper has better performance metrics because of the application of component connectivity.

VI. CONCLUSION

To make network virtualization an integral part of the future Internet architecture, efficient and practical algorithms for VN embedding are specially required. In this paper, we propose a robust VNE Algorithm based on component connectivity in large-scale network which differs from the previous algorithms.We argue that component connectivity applied in our algorithm can greatly increase the solution space and the quality of the heuristic algorithms. To this end we first formulate the embedding problem. And then we put k-core theory and load balancing into our algorithm.The simulation shows that our algorithm can get better acceptance ratio, average revenue and cost at complex VN requests. However,there are a number of places that can be improved like there is some residual substrate resource that can be used.

ACKNOWLEDGMENT

This work was supported in part by the National Natural Science Foundation of China under Grant No.61471055.

[1] Zhang C, CUI Y, Tang H, et al, “State-of-the-Art Survey on Software-Defined Networking (SDN),”Journal of Software, 2015, pp. 1-006.

[2] Sköldstr öm P, Yedavalli K, “Network virtualization and resource allocation in openfl ow-based wide area networks,” Proc. Proceedings of International Conference on Communications (ICC),2012, pp. 6622-6626.

[3] Akhunzad a A, Gani A, Anuar N B, et al, “Secure and Dependable Software Defined Networks,”Journal of Network & Computer Applications,2015.

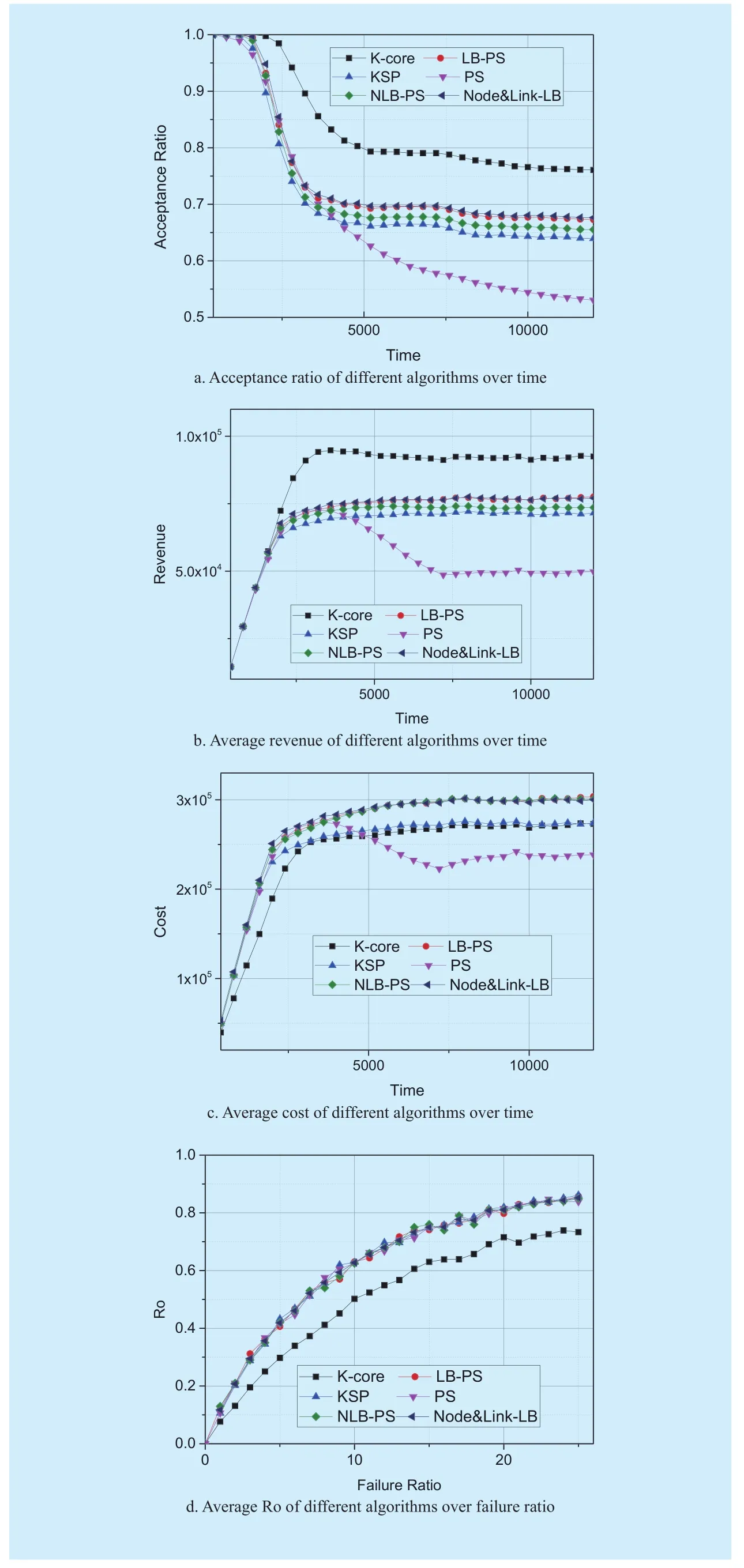
Fig. 8 Performance metrics under different algorithms

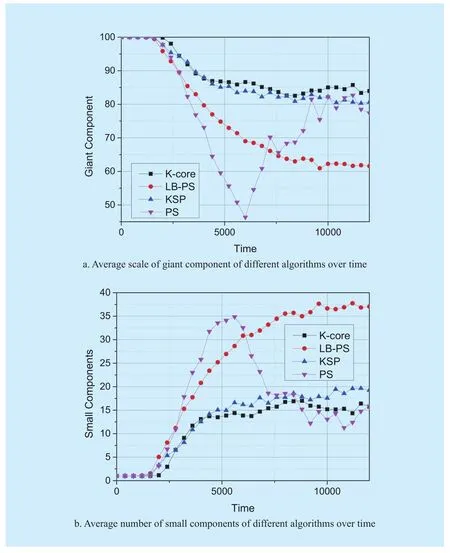
Fig. 9 Analysis of component connectivity

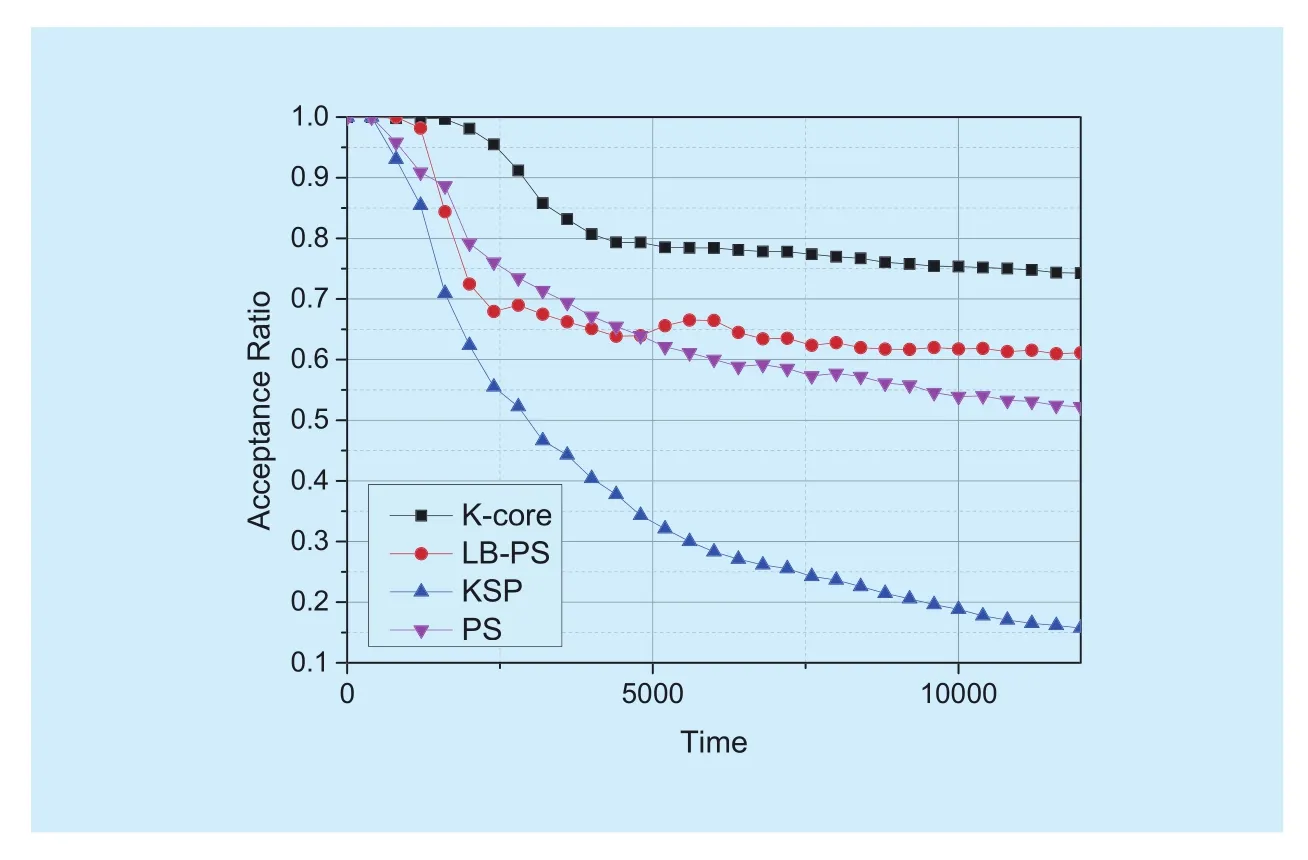
Fig. 10 Acceptance ratio of four algorithms over time under extreme BA network

[4] Liu Y, L i Y, Wang Y, et al, “Optimal Scheduling for Multi-Flow Update in Software-Defined Networks,” Journal of Network & Computer Applications, 2015, 54(C), pp. 11–19.

[5] Suzuki, Kazuya, et al. “A Survey on OpenFlow Technologies.” Ieice Transactions on Communications, E97.B.2, 2014, pp. 375-386.

[6] Zuo, Qing Yun, et al. “Research on Open-Flow-Based SDN Technologies.” Journal of Software, vol. 24, no. 5, 2013, pp. 1078-1097.

[7] Yu, Minlan, et al. “Rethinking virtual network embedding:substrate support for path splitting and migration.” Acm Sigcomm Computer Communication Review, vol. 38, no.2, 2008, pp. 17-29.

[8] Chowdhur y N M, Rahman M R, Boutaba R, “Virtual network embedding with coordinated node and link mapping.” Proc. International Conference on Computer Communications (INFOCOM),2009, pp. 783-791.

[9] Wang Z, Wu J, Wang Y, et al, “Survivable Virtual Network Mapping using optimal backup topology in virtualized SDN,” China Communications,vol. 11, no.2, 2014, pp. 26-37.

[10] Anderse n D G, “Theoretical Approaches To Node Assignment.” Computer Science Department, 2002.

[11] Fan J, Ammar M H, “Dynamic Topology configuration in Service Overlay Networks: A Study of Reconfiguration Policies,” Proceedings of International Conference on Computer Communications (INFOCOM). IEEE, 2006, pp. 1 - 12.

[12] Lu J, T urner J, “Effi cient Mapping of Virtual Networks onto a Shared Substrate.” Washington University in St Louis, 2006.

[13] Jarray A, Karmouch A, “Decomposition approaches for virtual network embedding with one-shot node and link mapping,” Networking IEEE/ACM Transactions on, vol. 23, no. 3, 2015,pp. 1012-1025.

[14] Hsu W H, Shieh Y P, Wang C H, et al, “Virtual Network Mapping through Path Splitting and Migration,” Proceedings of Advanced Information Networking and Applications Workshops(WAINA), 2012, pp. 1095-1100.

[15] Liu J, Huang T, Chen J, et al, “A new algorithm based on the proximity principle for the virtual network embedding problem,” Journal of Zhejiang University SCIENCE C, vol. 12, no. 11, 2011,pp. 910-918.

[16] Tao H, Jiang L, Jianya C, et al, “A topology-cognitive algorithm framework for virtual network embedding problem,” Communications, China,vol. 11, no. 4, 2014, pp. 73-84.

[17] Chen Q, Wan Y, Qiu X, et al, “A survivable virtual network embedding scheme based on load balancing and reconfiguration,” Proceedings of Network Operations and Management Symposium (NOMS), IEEE, 2014, pp. 1-7.

[18] Jiang L I U, HUANG T, CHEN J, et al, “New algorithm for hub-and-spoke topological virtual networks embedding problem,” The Journal of China Universities of Posts and Telecommunications, vol. 19, no. 1, 2012, pp. 55-61.

[19] Lischka J, Karl H, “A virtual network mapping algorithm based on subgraph isomorphism detection,” Proceedings of the 1st ACM workshop on Virtualized infrastructure systems and architectures, 2009, pp. 81-88.

[20] Cheng X, Su S, Zhang Z, et al, “Virtual network embedding through topology-aware node ranking,” ACM SIGCOMM Computer Communication Review, vol. 41, no. 2, 2011, pp. 38-47.

[21] Dorogovtsev, S. N., A. V. Goltsev, and J.F. Mendes. “k-Core organization of complex networks. “ Physical Review Letters 96.4(2006):040601.

[22] Dianati N, “Unwinding the hairball graph: pruning algorithms for weighted complex networks,”Eprint Arxiv, 2015.

[23] Frieze A, Krivelevich M, Martin R, “The emergence of a giant component in random subgraphs of pseudo-random graphs,” Random Structures & Algorithms, vol. 24, no. 1, 2004, pp.42–50.

[24] Beck M T, Fischer A, Botero J F, et al, “Distributed and scalable embedding of virtual networks,”Journal of Network & Computer Applications,2015, 56(C), pp.124-136.

[25] Zhang Z, Su S, Zhang J, et al, “Energy aware virtual network embedding with dynamic demands: online and oラine,” Computer Networks,2015, 93: 448-459.

[26] Chang X L, Mi X M, Muppala J K, “Performance evaluation of artificial intelligence algorithms for virtual network embedding,” Engineering Applications of Artificial Intelligence, vol. 26, no.10, 2013, pp. 2540-2550.

[27] Coniglio S, Grimm B, Koster A M C A, et al, “Optimal offline virtual network embedding with rent-at-bulk aspects,” Computer Science, 2015.

[28] Chen Q, Wan Y, Qiu X, et al, “A Survivable Virtual Network Embedding scheme based on load balancing and reconfiguration,” Proc. NOMS 2014 - 2014 IEEE/IFIP Network Operations and Management Symposium, IEEE, 2014, pp. 1-7

[29] Z Jun，M Zhong, “Virtual network mapping algorithm based on load balancing multi-objective particle swarm optimization,” Proc. 11th International Conference on Wireless Communications, Networking and Mobile Computing(WiCOM 2015) IEEE, 2015, pp. 5-5.