基于Aho-Corasick自动机算法的概率模型中文分词CPACA算法

徐懿彬



基于Aho-Corasick自动机算法的概率模型中文分词CPACA算法

徐懿彬

(女王大学工程与应用科学学院加拿大安大略省金斯顿市 K7L 3N6)

Aho-Corasick自动机算法是著名的多模式串匹配算法，它在模式串失配时，通过fail指针转移至有效的后续状态，存在一个或多个有效的后续状态可能。据此特性，该文提出了一种适应于中文分词的自动机算法。该算法使用动态规划的方法，计算上下文匹配概率，转移至最佳的有效后续状态，即实现了基于字符串匹配的机械分词方法与基于统计概率模型的方法结合。实验结果表明，该算法分词准确率高。

AC自动机; 中文分词; 动态规划; Trie树

词是最小的能独立运行的语言单位，因此中文分词是自然语言处理的第一步，它广泛应用于机器翻译、搜索引擎、拼音输入法、文章关键词提取、汉语语音合成、数据挖掘等领域。中文分词主要可以分为机械分词和统计学分词两类。

机械分词利用词典作为主要的资源，将字符串以特定规则与词典中的词条比对，得出切分方案。此类分词方法根据扫描方向和匹配规则的不同，有最大正向匹配法、最大逆向匹配法、最小切分法等，但此类分词方法有两个缺点：1) 对交集型歧义、组合型歧义和真歧义三类歧义句子的检测、纠正能力低：使用正向最大匹配法的错误分词率为1/169，逆向最大匹配法的错误切分率为1/245[1-2]；2) 分词准确性和效率受到词库容量的约束。为解决这两个问题，近年来已有诸多方法被提出，文献[3]和文献[4]分别提出了一种消除交集型歧义的方法；文献[5]给出了一种基于分词排序的消除歧义算法；文献[6]提出了一种基于最大匹配法、取得96.7%分词准确率的算法。

统计学分词是根据模式串在字符串中与上下文联合出现的概率来构建统计模型，从而决定分词的方案。统计分词方法不受词库容量大小的约束，能有效地减小切分歧义、识别未登录词(新词、怪词)。但在跨领域方面存在不足，需要针对不同领域进行不同的语料训练。此类分词算法有如互信息、N元文法模型、神经网络模型和隐马尔可夫模型等[7]；统计学分词的算法有如文献[8-10]等。可根据是否需要人工处理过的语料，将统计学算法分为监督学习模型和无监督学习模型两种。有监督学习模型需要大量人工处理过的语料，取得准确的语料需要很高的人力物力，而无监督学习模型可以轻易地使用大量未经处理过的资源，但就分词准确率而言，文献[11]提出的通过改进VE算法并结合BVE和MDL (minimum description length)是VE算法中最好成绩的算法，以及文献[12]提出的ESA被认为是目前中文语料上效果最好的无监督分词方法[13]，这些算法的分词准确度相较于有监督学习模型的分词效果还有一定差距[11-13]。

通常，词典和未处理过的语料等材料可以轻易地获取，如果可以把有监督分词、无监督分词方法和机械分词方法结合起来，则可以在分词准确率与语料规模之间找到平衡点。

为更好地提高中文分词的准确度，本文提出基于Aho-Corasick automation(AC自动机)的概率模型中文分词CPACA算法(a Chinese word segmentation algorithm of probability model based on Aho-Corasick automata algorithm)，采用动态规划的方法处理，结合上下文来失配转移，同时使用无监督学习语料与有监督学习语料，将基于统计的分词法与基于字符串匹配的分词方法相结合，加强了消除歧义、识别未登录词的能力，提高了分词的准确度。

1 相关概念

定义1 交集型歧义和组合型歧义：设字符串=12…A…A+m…A…A+n…A(,,,∈{|1≤≤,∈+},-≥2，+表示自然数集)，其中A表示字符串中第个字符(∈[1，])。令的子串1=…+…，2=+……+，3=1∩2(3≠)。如果满足S1、S2皆为词，则称为交集型歧义字符串。令的子串3=…+n，4=+…，(3Ì4)如果满足3是词，4也是词，则称为子集型歧义字符串。

定义2 结点路径和结点长度：从根节点(root)到某个特定结点，经过的结点集合称为这个结点的结点路径。经过结点的总数称为这个结点的结点长度。

定义3 后缀结点：设结点E，若存在结点E，使得E∈({E,E})，都有–≥0，则称E为E的后缀结点。其中，结点E的路径为123…a；结点E的路径为123…b(<)，且满足a=b,∈{|1≤≤,∈N}；结点E路径为12⋯c(<)，且满足a=c,∈{|1≤≤,∈N}。

定义4 匹配点和匹配性：若一个结点的结点路径与一个模式串的结点路径相等，称这个结点为匹配点。对于一个结点，如果它是匹配点或者它的后缀结点是匹配点，则认为该结点具有匹配性。

定义5 有限自动机[14]：一个五元组=(,,,0,) 称为五元组自动机，其中：是状态的有限集合(所有Tire 树上的结点)；是有限输入字母表(模式串集合)；是一个从×到的函数，称作的转移函数，这个函数指向下一个状态；0∈指的是初始结点(Tire树上的根结点以及无关点)；∈指的是自动机上的匹配点(接受状态)。

定义6 最长后缀模式子串[14]：设有结点E，若E∈，E∈({E,E})，都有–≥0，则12…b构成的串叫作结点E的最长后缀模式子串；定义结点E结点E的模式后缀结点。其中，结点E的路径为12…a；结点E的路径为12…b(<)，且满足a=b,∈{|1≤≤,∈N}，并使得12…b构成的串是模式串集合中的一个串；结点E的路径为12…c(<)，同时满足a−=c,∈{|1≤≤,∈}，并让12…c构成的串是模式串集合中的一个串。

定义7 耦合度和存在度：在封闭语料库(有监督)中，分别以表示结点路径、结点路径出现的次数，表示结点路径与结点路径作为两个相连的词出现的次数，令，则称为与的耦合度。在开放语料库(无监督)中，分别以表示结点路径、结点路径出现的次数，表示结点路径与结点路径相连出现的次数，令，则称为与的存在度。

2 CPACA中文分词算法

2.1 CPACA中文分词算法的定义及步骤

定义8 CPACA中文分词算法：设字符串=12…A(∈+)，其中A表示字符串中第个字(∈[1,])；设A的匹配点集合为T=12…B(∈+)，T按结点长度降序排序，匹配点集合使用Aho-Corasick Automation算法取得，表示分词进行到个字符时，恰以T的第个匹配点B为结尾的匹配概率，；表示B对应的结点路径；表示B的结点长度(∈[1,])。的匹配概率为：，其中，为的匹配点集合中选中的匹配点编号，对于每个：1) 当时，temp=0；2) 当时，，其中，g为的匹配点总数，为的匹配结点集合中选中的匹配点编号。根据统计概率，当时，需考虑两种可能性：①当前模式串和选定的前一个词为词与词的关系；②当前模式串与选定的前一个词共同组成一个词。当时，即当前模式串B与选定的前一个词共同组成的词的长度小于或等于T的最长后缀模式子串长度，则仅考虑可能性。在的情况下，设B与选定的前一个词共同组成的词存在，则这个词为新词的可能性很小，如设“勤奋”“刻苦”是既有的词，同时，“勤”“奋”“刻”“苦”也分别以单字词的形式存在，出现由“奋”“刻苦”组成的未登录词“奋刻苦”使“勤奋”/“刻苦”被切分成“勤”/“奋刻苦”的可能性很小，并且如“勤”“奋”组成“勤奋”也已为既有词。故这种情况下即使能组成合法的词，极大概率下也是模式串11…B-1中的一个，并非新词且已经计算过概率了，所以仅需考虑可能性②。综上，分词进行到个字符时，恰以B为结尾的分词方案为#分隔符或+#分隔符。称使用上述方法取得分词方案的算法称为CPACA中文分词算法。

CPACA算法属于机械切分算法，也符合基于统计模型算法的定义。CPACA算法分为4个步骤：1) 语料训练，2) Trie 树构建，3) 自动机构建，4) 字符串分割。

2.2 语料训练

语料训练分为封闭语料库训练(有监督)与开放语料库训练(无监督)，其中，训练封闭语料库即给定已完成切分操作的文段，作为语料，在语料中逐词计算当前词与上一个词作为词与词的关系，同时出现的次数，生成CP函数所需的语料库；开放语料库的语料为未进行切分操作的文段，逐字符计算当前字符或词与上一个字符或词同时出现的次数，生成OP函数所需的语料库。语料训练算法的本质是在线性扫描给定数据时，将当前词的模式串编号与下一个词的模式串编号同时作为语料库的索引，累加词语同时出现的次数。封闭语料库训练数据来源有如1998年1月《人民日报》语料库(PKU)等；开放语料库的数据可以为任意文段；开放语料库规模越大则未登陆词识别准确度越高。本算法不涉及语料制作。语料训练在现实操作中可用STL中的MAP库或再建一棵Trie树，线性遍历数据，可与本算法中建立Trie树的操作同时进行，记录结点路径两两联合出现的次数。查询时间复杂度可控制在(1)。

2.3 Trie树构建

将所有模式串依次逐字符插入Trie树中，插入过程中若在路径中已存在指向当前字符的结点，则访问到该结点，如无相对应的结点，则新建一个指向当前字符的结点，若一个模式串完成插入，标记其路径中最后一个结点。

Trie树在初始状态时，仅含有一个结点root(根节点，root的编号为0)，设模式串=12…C，当前字符C在Trie 树中的结点编号为now[]，C所在结点的子结点中通过C+1转移到的状态结点编号为next(now[],C+1)，初始状态为now[C]=next(now[0],C)；通式为now[C+1]=next(now[C],C+1)，当now[C+1]=Null时，即当前无相对应结点，则创建新的结点，并用新的结点编号赋值now[C+1]和next(now[C],C+1)；当且仅当当前完成了一个模式串的插入，mp[now[C]]表示当前模式串编号的映射。done[now[C]]=True，length[mp[now[C]]]的值为该模式串的长度，mp[now[C]]的值为当前模式串的编号，link[now[C]]表示当前以C为结尾的结点的最长后缀模式子串的结尾结点编号。将树上所有结点的link[now[C]](后缀子串链表)赋值为-1。反复执行以上所有过程，完成插入所有模式串后，Trie 树构建完毕。

实例：

创建模式串集合P={“独立”“独立自主”“自主”“自主权”“自主平等”“平等”“平等互利”“互利”“互利互惠”“互利合作”“和平”“原则”“五项原则”“立”“主”，“等”“权”“利”“惠”“合”“作”“则”“项”}。如图1所示，灰色结点表示匹配点(该节点的done为真)。

2.4 自动机构建

通过广度优先遍历整棵树，根据KMP算法，得到每一个结点的指针fail并构建后缀子串链表。自动机在主串扫描失配时，fail指针指向失配情况发生后的可行情况(后缀结点)。设now结点的后缀结点fail(now)的模式串结束标志为true,即done[*fail(now)]=true，则link[now]=fail(now)，否则，link[now]=link[*fail(now)]。

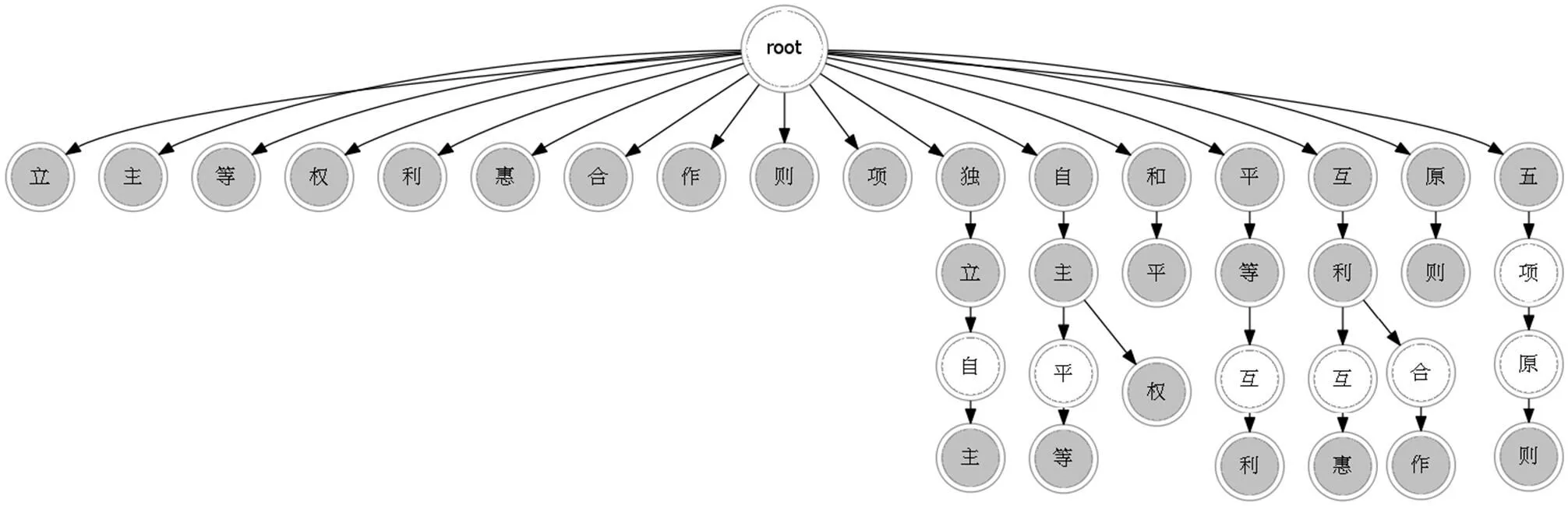
图1 Trie 树图

从任意一个结点now来看，首先遍历now的子字符集合，设存在通过now转移的子结点，则将该子结点的编号加入到搜索队列然后计算link(now)，再对该结点的后缀子串链表信息进行更新。否则，计算fail(next(now,))的值。构建完成后，得到全部结点的最长后缀模式子串的结点编号以及失配指针fail。

实例 模式串集合中构建自动机后，黑色虚线箭头指向fail指针指向的对象，灰色虚线箭头指向link指针指向的对象，工作原理如图2所示。

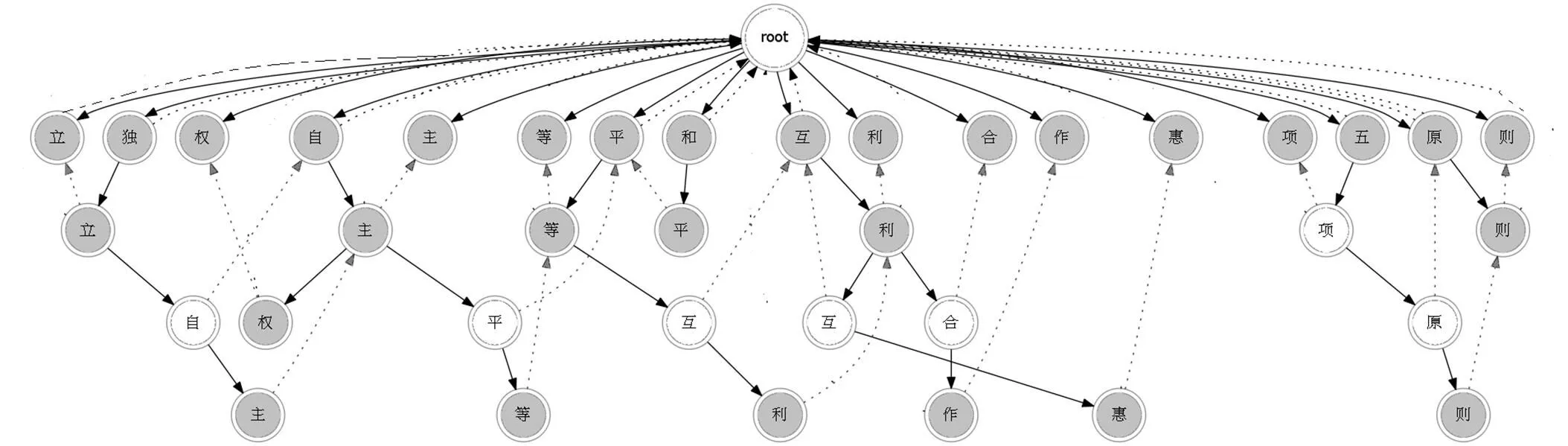
图2 自动机工作原理图

2.5 字符串分割

字符串分割的算法是CPACA算法的关键部分，从自动机的0(起始状态)开始，以字符串中每个字符为依据进行转移，逐字符遍历其最长后缀模式子串集合直至根节点，计算当前匹配点与上文联合出现的概率，直到完成字符串的匹配。

在字符串分割的过程中，设字符串=12…t。从0(初始状态)开始，使用函数move(q,t+1)进行状态转移，再使用后缀子串链表信息，更新模式串的匹配信息。归功于五元组自动机的预处理结果，在move(q,t+1)失败的时候，当前指针直接转移到后继结点上，继续匹配(next(q,t+1)存储了后继结点编号)。在遍历文本时，通过指针link找到所有的后缀模式子串、计算匹配概率。当文本遍历结束后，便得到了最优的分词方案(程序语句见算法3)。由于字符串规格与语料库规格的扩大，匹配概率也增大，故现实应用中应采用长整型存储或者高精度存储方式。

实例 使用模式串集合P对字符串“独立自主和平等互利”进行分词，运用CPACA算法，从0(初始状态)开始，进行状态转移，直至字符串分词完毕，字符串分词过程如表1所示。

表1 字符串分词过程

续表

步骤切分结果Cur切分过程 独立/自/主主D[3][1]+D[4][2]<=D[4][1]P[4][2]=max(P[3][1]×CP(自，主))； 5独立/自主/和和D[4][1]+D[5][1]>D[5][1],D[4][2]+D[5][1]>D[5][1]P[5][1]=max(P[4][1]×CP(自主,和), P[4][2]×CP(主,和),P[2][1]×OP(自主,和), P[2][2]×OP(自主,和), P[3][1]×OP(主,和))； 6独立/自主/和平和平D[6][1]+D[4][1]>D[6][1],D[6][1]+D[4][2]>D[6][1]P[6][1]=max(P[4][1]×CP(自主,和平), P[4][2]×CP(主,和平),P[2][1]×OP(自主,和平),P[2][2]×OP(自主,和平),P[3][1]×OP(主,和平))； 独立/自主/和/平平D[6][2]+D[5][1]<=D[6][1]P[6][2]=max(P[5][1]×CP(和,平))； 7独立/自主/和/平等平等D[7][1]+D[5][1]>D[7][1],D[7][1]P[7][1]=max(p[5][1]×CP(和,平等),P[4][1]×OP(和,平等),P[4][2]×OP(和,平等)) 独立/自主/和平/等等D[7][2]+D[6][1]>D[7][1],D[7][2]+D[6][2]<=D[7][1]P[7][2]=max(max(P[6][1]×(CP(和平,等)), P[6][2]×(CP(平,等)),max(P[4][1]×OP(和平,等),P[4][2]×OP(和平,等)))； 8独立/自主/和/平等/互互D[8][1]+D[7][1]>D[8][1],D[8][1]+D[7][2]>D[8][1]P[8]=max(P[7][1]×CP(平等,互), P[7][2]×CP(等,互),P[5][1]×OP(平等,互),P[6][1]×OP(等,互),P[6][2]×OP(等,互))； 9独立/自主/和/平等互利平等互利D[9][1]+D[5][1]>D[9][1]P[9][1]=max(P[5][1]×CP(和,平等互利),P[4][1]×OP(和,平等互利),P[4][2]×OP(和,平等互利))； 独立/自主/和平/等/互利互利D[9][2]+D[7][1]<=D[9][1],D[9][2]+D[7][2]<=D[9][1]P[9][2]=max(P[7][1]×CP(平等，互利), P[7][2]×CP(等，互利))； 独立/自主/和平等/互/利利D[9][3]+D[8][1]<=D[9][1]P[9][3]=max(P[8][1]×CP(互，利))； 10独立/自主/和/平等互利—P[9][1]>P[9][2]>P[9][3]

3 歧义消除分析

3.1 歧义分词问题

目前存在的交集型歧义、组合型歧义和真歧义中，除了真歧义是不可避免的外，交集型歧义(如“脑海里”，可被分为{“脑”“海里”}和{“脑海”“里”})和组合型歧义(如“才能”，在句子“杰出的才能”和“有他才能胜出”中可被分为{“才”“能”}或{“才能”})是可以避免的。产生歧义的原因都是因为存在多种切分可能性，而计算机采取了错误的切分。切分具有后效性，因此，一处切分错误常导致全文分词错位，因此能否较好地解决歧义分词问题是衡量分词算法性能好坏的重要标准。

3.2 歧义消除

temp=0时进行。例如，“脑海里”这个交集型歧义词，现在采用CPACA算法对第个字符(里)进行切分，则(脑海里)=max(´CP(“脑”“海里”)，´CP(“脑海”“里”))；对于“杰出的才能”和“有他才能胜出”这两个子集型歧义词，设当前对第个字符(能)进行切分，则{杰出的才能}= max(´CP(“的”“才能”)，(x-1,t)´CP(“才”“能”))和{有他才能胜出}=max((x-2,t)´CP(“才能”“胜出”)，(x-2,t)´CP(“能”“胜出”))。结合上下文，将所有存在的切分可能性进行比较，取正确几率最高的一种，因此，可保证输出结果为全文分词正确率最高的方案。这样既解决了机械分词方法中存在的歧义问题，同时又解决了基于概率模型“无词库”对常用词的识别精度差的问题，提高了概率模型的识别准确度。

3.3 未登录词识别

可将未登录词分为4类：1) 形态上发生变化的词，如漂漂亮亮是漂亮的叠词；2) 固定表达，如“三百次”“一百天”；3) 命名实体，如“毛泽东”“习近平”；4) 新词，如“阅兵蓝”“学霸”。大多数情况下这些词语切分错误不会影响上下文识别，如“学霸的世界我不了解”在不进行未登录词识别时，切分结果为“学/霸/的/世界/我/不/了解”，除了“学霸”切分错误外，下文并未出现切分错位的情况。相较其他切分算法，CPACA较为容易检测出未登录词，根据定义8中处理未登录词的转移方程：

当两个字符串、叠加在一起的长度大于字符串的匹配点的最长后缀模式子串()，即、组成一个词的记录在封闭语料库里不存在，则组成的词有一定可能性是一个未登录词，则将、的耦合度CP(,)与、的存在度OP(,)对比，若存在度高于耦合度，则认为的组合为未登录词。这种方法将机械切分、无监督模型概率与有监督模型概率实时对比，有效地提高了识别的准确度。

4 CPACA算法在拼音分词中的使用

英文单词间用空格隔开，不具有歧义性，但拼音串没有音节与音节间隔离的标准，如拼音串“xian”可以划分为“xi an”(代表“西安”及其同音词)，也可以划分为“xian”(表示“先”及其同音词)。对于拼音串中一段的切分错误可能会导致一整个句子出现问题，如“xianggangren”原意为“香港人”，如第一个音节被分解为“xi an”，无论后文如何切分都无法得出正确结果。诸如此类的问题使得计算机在分解、识别拼音串和拼音输入法连拼时产生麻烦。就此，根据CPACA算法，从统计的角度出发，当拼音串只为“xian”时，使用者想表达“西安”的概率远高于“先”，但对于“woxianqushangxue”，翻译为“我先去上学”的几率远高于“我西安去上学”，即在概率模型中，“xian”与“qu”组合的可能性高于“xi”“an”“qu”。采用CPACA算法的拼音输入法可以长期学习输入者输入的语句，丰富统计模型，最大程度上减少了拼音分词的错误，使得拼音分词愈发精准。

5 理论时间复杂度

设||表示字母表的规模，是字符串规模，表示模式串的数量，M表示第个模式串的长度，模式串的规模总共为，表示号模式串的后缀模式子串链表长度，最长后缀模式子串总指针规模为。

5.1 预处理

预处理这个阶段主要包括Trie树的建立和AC自动机的构建。在建立Trie树时，将每个结点都赋值为初态，这时空间规模为字母表规模，可见在Trie树建立过程中，最坏的时间复杂度是；在使用广度优先规则，遍历Trie 树时(构建AC自动机)，同样对每个结点进行询问，故遍历Trie 树的最坏时间复杂度同样也为。

5.2 分 词

分词过程中，文本指针不会回溯，且保持移动为线性，枚举后缀模式子串的时间复杂度为，CP函数与OP函数枚举每个模式子串之前的匹配可能性的最坏时间总复杂度为，自动机状态转移是O(1)时间复杂度，所以，字符串分词过程的最坏时间复杂度为。

6 实验仿真

本文实验使用一台HP-Z800 服务器(英特尔四核处理器X5570，内存为3 GB，操作系统为Noi Linux)。

6.1 分词效果实验

有监督训练数据采用Sighan 2005 bakeoff分词语料中由北京大学标注的数据，对CPACA所需的耦合度数据库进行训练，存在度数据库的数据取自搜狗新闻语料(120 MB)。采取十折交叉验证，在分词实验中，首先将北京大学语料库随机平均分成10份，任意选取其中1份作为测试数据，9份作为耦合度训练数据，将分词实验步骤重复10遍，得到10次实验结果，再与已有算法的分词效果进行对比，评测分词效果的指标有以下4个(表示召回率、表示准确率、1为F-值、为未登录词召回率)：

(2)

(3)

碍于篇幅，本文将前5次结果与后5次结果分别取平均数据，结果如表2所示。参与比较的算法是：改进的逆向最大匹配算法[2](算法A)、消除中文分词中交集型歧义的方法[3](算法B)、改进的正向最大匹配算法[5](算法C)、基于粗分和词性标注的中文分词方法[7](算法D)、表示学习算法[8](算法E)、改进概率统计算法[9](算法F)、树形结构算法[15](算法G)、带词长词典与判断消除算法[16](算法H)。此外，就合计准确率而言，可进行比较的分词方法有：Sighan2005最佳成绩(封闭)，Sighan2005最佳成绩(开放)，它们的合计准确率分别为94.6%和96.8%[8]。

从表2所示的数据可以看出，CPACA算法的准确率达到95%以上，对歧义字段有很好的消除效果，通过与近年提出的方法相对比，说明该方法具有较高的准确度。导致错误切分的原因主要有：1) 字符串中含有过分生僻人名或部分罕见地名；2) 字符串中含有古汉语；3) 字符串中存在错别字。

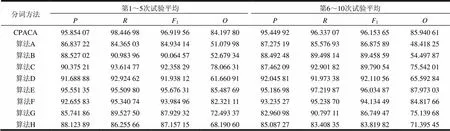
表2 实验仿真结果

6.2 分词时间效率实验

在不同的文本长度下，不同算法的分词耗时比较如图3所示，实验数据从“腾讯大闽网”抓取，为2014年全年福建本土新闻稿随机组合形成；耦合度数据库规模和存在度数据库规模皆为固定的150万词(随机生成)。

从图3可见，CPACA算法分词速度在所有参加测试的算法中排第4位，与准确率相近的算法E、算法F、算法C相比具有较大优势。并且，这种优势伴随数据规模的增大而愈发明显。由此可见CPACA算法适用于屏蔽词检测或网页搜索等需高准确率且流量巨大的工程当中。

图3 分词耗时比较

7 结束语

在AC自动机的基础上，提出了CPACA中文分词算法。经过实验验证，CPACA算法不仅具有很好的实用性，而且在字符串规模大、模式串规模大、数量多的现实情况下，提高了分词的准确率。

CPACA算法分词准确率很大程度上取决于耦合度与存在度，两者的语料库丰富与否都是分词准确率的决定性因素，但目前存在封闭语料库规模小的问题，华人打字习惯主要以拼写词组或短语的方式，鲜少一次性拼写一整个句子，因此，今后可研究拼音、五笔等输入法如何在用户输入的同时自动获取文段的分词方案。在拼音输入法中加入切分记录的功能，建立如云语料库等方法，使封闭语料库也可通过无监督的方式来自我学习、自动更新，及时加入新近未登录词，从而进一步提高中文分词的准确率。

CPACA算法在一定程度上使得中文分词更加准确，但随着字符集、模式串的增大，导致算法所需的空间不断加大，因此，后续研究将在保证准确率的基础上，研究怎样减小该算法的空间复杂度。

[1] 魏莎莎, 熊海灵. 中文分词中的歧义识别处理策略[J]. 微计算机信息, 2010, 30: 190-192.

WEI Sha-sha, XIONG Hai-ling. Ambiguity identification strategy of Chinese word segmentation[J]. Control & Automation, 2010, 30: 190-192.

[2] 罗桂琼, 费洪晓, 戴弋. 基于反序词典的中文分词技术研究[J]. 计算机技术与发展, 2008, (1): 80-83.

LUO Gui-qiong, FEI Hong-xiao, DAI Yi. Research of Chinese segmentation based on converse segmentation dictionary[J]. Computer Technology and Development, 2008(1): 80-83.

[3] 魏博诚, 王爱平, 沙先军, 等. 一种消除中文分词中交集型歧义的方法[J]. 计算机技术与发展, 2011, 21(5): 60-63.

WEI Bo-cheng, WANG Ai-ping, SHA Xian-jun, et al. A method about removing overlapping ambiguity producing in Chinese matching[J] Computer Technology and Development, 2011, 21(5): 60-63.

[4] MA Guo-jie, LI Xing-shan, RAYNER K. Word segmentation of overlapping ambiguous strings during chinese reading[J]. Journal of Experimental Psychology-Human Perception and Performance, 2014, 3(40): 1046-1059.

[5] JIANG W, GUAN Y, WANG X. A pragmatic Chinese word segmentation approach based on mixing models[J]. Association for Computational Linguistics and Chinese Language Processing, 2007, 11(4): 393-416.

[6] 李玲. 基于双词典机制的中文分词系统设计[J]. 机械工程与自动化, 2013(1): 17-19.

LI Ling. Design of chinese word segmentation system based on dual-dictionary mechanism[J]. Mechanical Engineering & Automation, 2013(1): 17-19.

[7] 姜芳, 李国和, 岳翔, 等. 基于粗分和词性标注的中文分词方法[J]. 计算机工程与应用, 2015, 51(6): 204-207.

JIANG Fang, LI Guo-he, YUE Xiang, et al. Segmentation of Chinese word based on method of rough segment and part of speech tagging[J]. Computer Engineering and Applications, 2015, 51(6): 204-207.

[8] 来斯惟, 徐立恒, 陈玉博, 等. 基于表示学习的中文分词算法探究[J]. 中文信息学报, 2013, 5(27): 8-14.

LAI Si-wei, XU Li-heng, CHEN Yu-bo, et al. Chinese word segment based on character representation learning[J]. Journal of Chinese Information Processing, 2013, 5(27): 8-14.

[9] SUN X, ZHANG Y, MATSUZAKI T, et al. Probabilistic Chinese word segmentation with non-local information and stochastic training[J]. Information Processing & Management, 2013, 49(3): 626-636.

[10] ZHANG D Y, XU Y. Chinese word segmentation based on the first kind of spline weight function neural networks[J]. Applied Science Materials Science & Information Technologies in Industry, 2014, 513-517: 683-686.

[11] HEWLETT D, COHEN P. Fully unsupervised word segmentation with bve and mdl[C]//Proceedings of ACL. [S.l.]: ACL, 2011: 540-545.

[12] WANG Han-shi, ZHU Jian, TANG Shi-ping, et al. A new unsupervised approach to word segmentation[J]. Computational Linguistics, 2011, 37(3): 421-454.

[13] 马宁, 李亚超, 何向真, 等. 一种实用的资源稀缺条件下的分词方法[J]. 计算机应用研究, 2016, 33(1): 68-70.

MA Ning, LI Ya-chao, HE Xiang-zhen, et al. Practical approach of word segmentation in poor resource situation[J]. Application Research of Computers, 2016, 33(1): 68-70.

[14] THOMAS H, CORMEN C E L, RONALD L R, et al. 算法导论[M]. 3版. 殷建平, 徐云, 王刚, 等, 译. 北京: 机械工业出版社, 2013.

THOMAS H, CORMEN C E L, RONALDLR, et al. Introduction to algorithms[M]. 3rd. Translated by YIN Jian-ping, XU Yun, WANG Gang, et al. Beijing: China Machine Press, 2013.

[15] 温唱. 基于树形结构的中文分词方法的研究与实现[D]. 北京: 华北电力大学, 2013.

WEN Chang. Research and implementation of Chinese word segmentation based on tree structure[D]. Beijing: North China Electric Power University, 2013

[16] 王崇. 基于带词长的词典机制和规则判定的歧义消解算法的中文分词技术的研究[D]. 青岛: 青岛科技大学, 2013

WANG Chong. Research on Chinese word segmentation technology with word length and rule algtithm[D]. Qingdao: Qingdao University of Science & Technology, 2013.

编 辑 税 红

A Probability Model Chinese Word Segmentation Algorithm Based on Aho-Corasick Automata Algorithm

XU Yi-bin

(Faculty of Engineering and Applied Science, Queen's University Kingston Canada K7L 3N6)

Aho-Corasick automata algorithm is a famous multi-string matching algorithm, which backtracks to the effective subsequence state through the fail pointer when it fails in one pattern matching, where one or more effective subsequent states may exist. According to the above characteristics, this paper proposes an automata algorithm suitable for Chinese segmentation. The algorithm calculates the context matching probability of the current pattern by dynamic programming method, and backtracks to the optimal subsequent state of maximum probability, namely, it can realize the combination of the mechanical Chinese segmentation and statistics and probability model. The experimental result shows that a high accuracy rate in Chinese segmentation can be obtained through this algorithm.

Aho-Corasick automation; Chinese segmentation; dynamic programming; trie tree

TP301.6

A

10.3969/j.issn.1001-0548.2017.02.018

2015-05-04；

2016-08-08

徐懿彬(1997-)，男，主要从事中文信息处理方面的研究.