太赫兹回旋脉塞的粒子模拟方法研究
2017-04-08刘大刚王重阳廖树清
刘大刚,王重阳,廖树清
太赫兹回旋脉塞的粒子模拟方法研究
刘大刚1,王重阳1,廖树清2
(1. 电子科技大学物理电子学院 成都 610054 ; 2. 中国工程物理研究院流体物理研究所 四川绵阳 621900)
分析了粒子模拟方法在模拟共形边界,特别是带此类边界的太赫兹回脉塞时引入计算误差的原因。给出了传统的共形网格差分算法的稳定性条件及两种通用的共形处理方法,并对两种方法的稳定性及准确性进行了分析。提出了一种新型的自适应共形网格剖分方法,该方法解决了共形网格的局限性问题。在有自主知识产权的全电磁粒子模拟软件CHIPIC上实现了该方法,并以一个圆柱波导验证了该方法的正确性。采用该方法模拟了工作于TE26模式的频率为0.42 THz的回旋脉塞及HE06模式0.22 THz准光腔回旋脉塞。
共性网格; 截止频率; 回旋脉塞; 粒子模拟; 太赫兹波
电子回旋脉塞(electron cyclotron resonate maser, ECRM)的研究和发展,是微波电子学中的一个重大突破,推动了一大类新型高功率毫米波、亚毫米波器件——回旋管的诞生。回旋管可填补传统微波器件和激光器在毫米波和亚毫米波段的缺口[1],其波段也可发展到太赫兹波领域。当工作波段位于太赫兹波段时,微小的工作波长将导致回旋脉塞结构尺寸的进一步缩小。因此,太赫兹回旋脉塞的工作性能对结构参数非常敏感,这对数值模拟的模型及算法精度提出了很高的要求。
另一方面,粒子模拟方法(PIC)是一种使用计算机来模拟电磁场与粒子相互作用问题的数值模拟方法。从电磁场算法上来看,该方法采用时域有限差分算法[2](finite difference time domain, FDTD),FDTD直接从概括电磁场普遍规律的麦克斯韦旋度方程出发,将其转换为差分方程组,是在一定体积内和一段时间上对连续电磁场的数据取样。因此,它是对电磁场问题的最原始、最本质、最完备的数值模拟,具有较广泛的适用性。从粒子算法上来看,PIC方法从洛伦兹、动量、冲量等定律出发来描述粒子在电磁场中的运动,其所计算的粒子运动行为是全面的,继而更能反映出实际的粒子运动规律。也正是因为PIC方法的以上特点,目前许多电真空微波源的研究者都将其作为数值模拟的首选方法。然而PIC方法中FDTD算法采用的是YEE网格模型,其在复杂边界建模上与实际结构的差异将可能降低模拟精度(主要体现在阶梯近似误差和网格数值色散误差),这在对结构参数较敏感的太赫兹回旋脉塞的模拟中是致命的。虽然阶梯近似误差和网格数值色散误差随着网格尺寸的减小而减小,但是网格尺寸的减小会使在模拟一定物理空间所需的总网格数急剧增加,以及保证算法稳定性所需的时间步长急剧减小,从而导致计算机所需存储空间和CPU计算时间急剧增大。
综上所述,要对太赫兹回旋脉塞进行准确高效的粒子模拟,必须对PIC方法中的FDTD算法有所改进。目前,国内外研究者采取的改进方法主要有3种途径:1) 加入并行算法;2) 采用交替隐式差分算法;3) 采用共形方法。并行算法通过多线程协作的方式来提高运算速度,但其缺点是随着线程数的增加,并行加速比将趋于饱和[3]。交替隐式差分方法通过放大时间步长的方法来提高运算速度,但时间步长增长将导致粒子运算的不稳定性[4]。共形方法[5]能在较大网格尺寸情况下,保证建模的准确性,从而以较快的运算速度得到较准确的模拟结果。目前,该方法在计算电磁散射等问题中得到广泛应用,但在粒子模拟领域使用较少。
1 自适应共形网格剖分方法
1.1 矩形网格模型缺陷
图1所示为矩形网格及共形网格对一斜渐变金属导体结构的拟合比较,其中黑影部分为导体区域,从图可看出当网格尺寸较大时,矩形网格将不能准确地反映该结构的斜渐变特性。图2所示为用矩形网格对一回旋脉塞建模的示意图。实线是设计尺寸,是建模后的互作用区长度,¢是实际设计的互作用区长度。很明显经过矩形网格剖分后,回旋脉塞互作用区长度变长,从而导致模拟出现较大误差。

a. 矩形网格拟合 b. 共形网格拟合

图2 回旋脉塞矩形建模剖面图
1.2 传统共形差分公式

如图3a所示,设一共形元胞其中黑色部分表示导体所占的元胞区域,白色表示真空所占元胞区域。在此元胞中,电场的递推公式保持不变,仍按照一般FDTD进行计算;而对于其磁场,则需按下式进行迭代[5]:
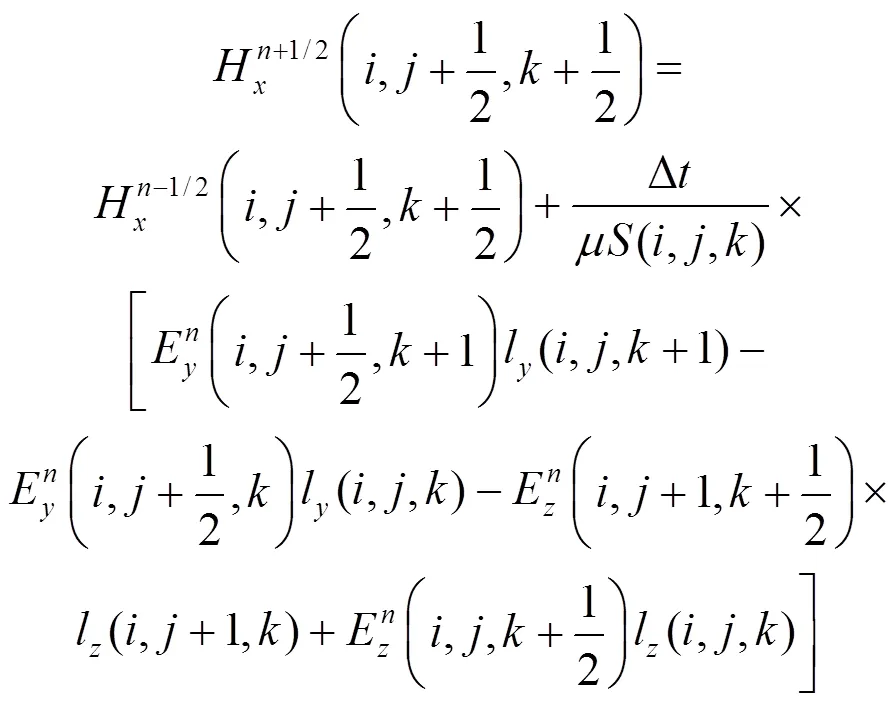
1) 共形元胞在导体外部的面积应该大于元胞总面积的5%,即该元胞相对面积(不含导体部分面积与总面积之比)要大于1/20;
2) 共形元胞中的最长相对边长(不含导体部分)与该元胞相对面积的数值比应小于12。
共形元胞的局限性主要体现在图3b和图3c所示的两种元胞模型中。对于此类元胞,要么不满足共形网格特性的制约条件1),要么不满足制约条件2),当用式(1)计算此类元胞时将出现畸变场,从而影响计算的稳定性。处理此类元胞的方法有两种[3],即后向加权平均的修正方法(MCFDTD)及相对面积修正方法(SC-FDTD)。MCFDTD方法的实质是将用式(1)计算出的当前时间步的电磁场与它上一个时间步的电磁场再作平均,以达到消除畸变场的目的。该方法在一定程度上会改善计算的稳定性,但需要在迭代时再对电磁场进行额外处理,增加了计算时间。另一方面,当畸变场过大时该方法还是不能满足计算的稳定性要求。SC-FDTD方法是将模拟区域内所有相对面积小于1/6的共形元胞的相对面积都近似为1/6。该方法在一定程度上也会改善计算的稳定性,但其影响了计算的准确性。因为许多满足共形限定条件的相对面积在1/20~1/6之间的共形元胞的相对面积都被当作1/6来处理,从而降低了模拟的准确性。
1.3 自适应共形元胞剖分

图4 共形边界拟合方法示意
图4所示为解决共形元胞限定问题的一种新型的共形元胞剖分方法。图4a所示为按实际共形边界剖分后所得共形元胞示意图,斜虚线是实际的共形边界,C1、C2、C3是按此边界剖分出的共形元胞,C1元胞将不满足共形限定条件。图4b所示为拟合后的效果示意,该方法的思路是在保证共形边界基本形状不变的前提下,适当增加不满足共形限定条件的元胞的边长,从而增加其共形面积以达到使其满足共形限定条件的目的。具体作法是:首先判断共形边界所在的元胞C1是否满足共形限定条件1),如果不满足,则按比率增加其共形边长直至满足共形条件1)。然后判断是否满足共形条件2),如果不满足则增加短边共形边长,直至满足共形条件2)。从图4b可看出,经过此处理后虽然也会引入一定的误差,但该方法是以共形限定条件作为依据来处理的,避免了SC-FDTD方法所引入的误差。另外,该方法处理过程主要在剖分元胞阶段进行,无需在迭代时增加额外的处理,也就弥补了MCFDTD的缺陷。
1.4 自适应共形元胞的模拟验证
本文采用直角坐标系,用自适应共形元胞及非共形元胞分别对圆柱波导中的TE11模进行模拟。圆柱波导半径10 mm,长20 cm,理论截止频率c= 8.797 654 GHz,如图5所示。模拟时,元胞尺寸大小为1 mm,在波导激励源[8]注入峰值功率为5 kW,模式为TE11的电磁波,如图5c所示。
图5 圆柱波导结构
图6a和图6b为注入频率为截止频率的1.1倍时的共形与非共形输出功率比较。从图可看出,由于输入频率大于截止频率,电磁场反射较小,输出功率接近于注入功率5 kW。
图6 自适应共形与非共形输出比较
从图6c和图6d可看出,当注入频率接近fc时,自适应共形计算输出平均功率接近于0,而非共形还有一定输出。这是因为非共形算法在拟合圆柱波导时是用矩形元胞拟合的,如图5b所示。这种拟合与自适应共形元胞拟合比较,拟合出的圆柱波导半径比实际半径偏差更大,且在圆周横截面上有更多毛刺所致。这就证明了在相同元胞步长情况下,自适应共形算法计算准确性比非共形高。
2 自适应共形网格模拟验证
2.1 TE06模式0.42 THz回旋脉塞的共形模拟
回旋脉塞的结构如图7a所示[7],其中为9 mm,为11 mm,为9 mm,为3°,为2°,为2.2 mm,电子注引导中心半径为1.15 mm,电子注横纵速度比为1.5,工作电流1.5 A,电压20 kV,互作用区磁场8.11 T。

模拟时为了保证边界条件封闭在脉塞左端、右端加入吸收边界条件,同时为了引出电子在脉塞左端设置一环状金属导体作为发射体,如图7b所示。

在图7b中,由于该脉塞工作于太赫兹频段,其结构尺寸偏小(径向总长不到3 mm),所以其径向及轴向的元胞剖分都很小。另外,为了降低磁场,该器件被设计成工作于二次谐波TE26模式上,这不仅要求必须是3维建模,而且要求要有更高的建模准确性,因为建模时误差过大将会导致该器件工作点的偏移[9-10]。
图8a和图8b所示为模拟所得模式分布图,图8c和图8d所示为模拟所得频谱及功率图。从模式分布图可看出,其工作模式在角向有两个周期,径向有6个半周期,其模式是TE26模式,从频谱及功率图可看出,其输出平均功率为7.8 KW左右,工作频率为0.419 4 THz,这与参考文献[7]中的结果图9基本吻合。
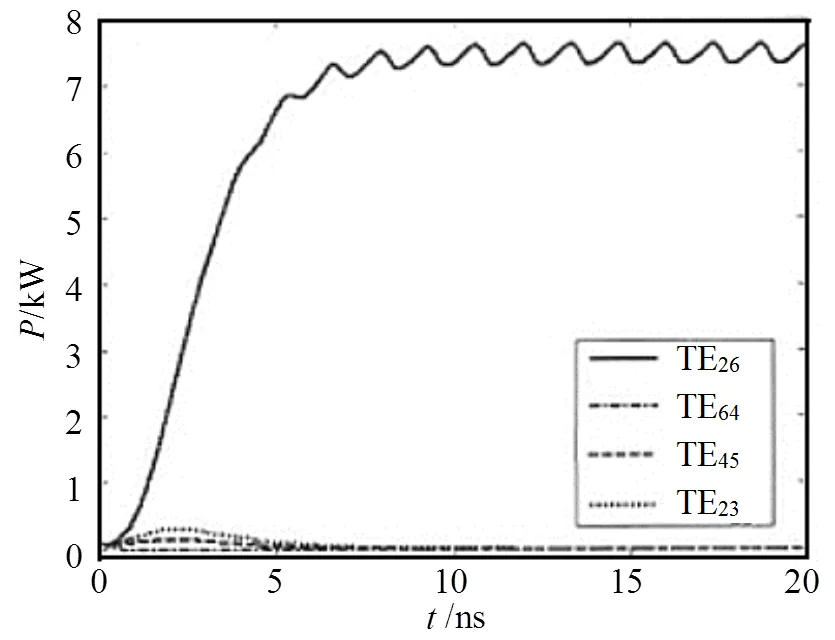
图9 各个模式下功率图
2.2 HE06模式0.22 THz准光腔回旋脉塞的模拟
该器件被设计成工作于HE06模式[11],工作频率为0.22 THz,输入功率60 W,放大输出功率10 KW。腔体结构由上下两个半径为4.52 mm的反射镜组成[12],如图10b所示。反射镜侧面有两个侧弧用于衍射返波,腔体总长57 mm,如图10a所示。

图10b和图10c分别是准光腔非共形与共形建模结果比较,由图可知矩形网格拟合时会引入较大的误差。由于此管工作频率较高,且属于放大类器件,此误差会导致工作点的偏移,使其工作于振荡模式,从而干扰放大器的正常工作。

图11是共形输出功率与频谱。由图11a与图11b可知,自适应共形拟合较好的保证了建模精度,从而使器件稳定工作于放大状态。
图12是非共形输出功率与频谱,矩形拟合时,由于误差的引入使得模式为HE05的返波振荡出现(图12a中频率191.2 GHz处),从而破坏了放大工作原理,最终导致输出功率的急剧下降,如图12b所示。

3 结束语
粒子模拟是研究粒子与电磁场相互作用的一种重要手段,它可以帮助研究人员认识和理解太赫兹回旋脉塞中的一些复杂的物理问题,也可以帮助研究人员优化相应器件的设计,从而使器件工作性能达到最优。然而,要对带有共形边界的太赫兹回旋脉塞进行电磁粒子模拟,如果采用标准的粒子模拟方法,要么保证不了必要的运算精度,要么使运算时间过长从而导致模拟无法完成。共形网格算法能较好的解决这一类问题,它能在较大的元胞尺寸下保证运算的精度,从而在较短的时间内模拟出正确结果。然而,共形算法亦有其局限性,本文在分析了标准时域有限差分法对共形边界模拟所引入计算误差的原因,以及两种通用共形处理方法的局限性基础上,提出了自适应共形剖分方法。该方法能在尽量减少误差的前提下,保证共形边界得以较准确地拟合,从而确保模拟的准确性。给出了工作于0.42 THz模式为TE26及工作于0.22 THz模式HE06的回旋脉塞算例,算例结果与文献给出的实验结果及理论推导结果基本稳合,进而证明了该方法的有效性。
[1] CHU K R.The electron cycltron maser[J]. Rev Mod Phys, 2004,76: 489-540.
[2] 王秉中. 计算电磁学[M]. 北京: 科学出版社, 2002.
全面标准化管理与服务业从业人员素质提升相辅相成,通过实施与宣贯标准体系,进行团队整体培训和管理经验的积累,提高从业人员的职业道德、知识水平、服务技能。多渠道开展服务业管理人员和从业人员的标准化知识培训,鼓励高校及科研院所与企业的联合共建工作,在服务业示范点设置标准化创新研究基地,培养既有标准化理论功底又有丰富标准化工作经验的人才。
WANG Bing-zhong. Electromagnetics calculation[M]. Beijing: Science Press, 2002.
[3] 廖臣, 刘大刚, 刘盛纲. 三维电磁粒子模拟并行计算的研究[J]. 物理学报, 2009, 58(10): 6709-6718.
LIAO Chen, LIU Da-gang, LIU Sheng-gang. Three- dimensional electromagnetic particle-in-cell simulation by parallel computing[J]. Acta Phys Sin, 2009, 58(10): 6709- 6718.
[4] LIU Shao-bin, LIU San-qiu. One-step alternating direction implicit FDTD algorithm[J]. Chin Phys B, 2004,13(11): 01892.
[5] 葛德彪, 阎玉波. 电磁波时域有限差分法[M]. 西安: 西安电子科技大学出版社, 2011.
GE De-biao, YAN Yu-bo. Finite-difference time-domain method for electromagnetic waves[M]. Xi¢an: Xidian University Press, 2011.
[7] 袁雪松, 鄢扬, 傅文杰, 等. 高次谐波太赫兹回旋管的多模工作研究[J]. 红外与毫米波学报, 2012, 31(4): 342-347.
YUAN Xue-song, YAN Yang, FU Wen-jie, et al. Multi- model high harmonic operation in a terahertz gyrotron[J]. Infrared Millim Journal of Infrared and Millimeter Waves, 2012, 31(4): 342-347.
[8] 周俊, 祝大军, 刘大刚, 等. 粒子模拟中波导激励源的设计与实现[J]. 强激光与粒子束, 2006, 18(12): 2019-2024.
ZHOU Jun, ZHU Da-jun, LIU Da-gang, et al. Deign and realization of waveguide excitation source in particle-in-cell simulation[J]. High Power Laser and Particle Beam, 2006, 18(12): 2019-2024.
[9] HAN Y, YUAN X S. Study of a grotron oscilltor withcorrugated interaction cavity[J]. Acta Phys Sin, 2012, 61(6): 64102-064102.
[10] 谢鸿全, 刘濮鲲. 等离子体填充波纹波导中低频模式特性分析[J]. 物理学报, 2004, 53(9): 3114-3118.
XIE Hong-quan, LIU Pu-kun. Analysis of the characteristics of low-frequency models in a corrugated waveguide filled with plasma[J]. Acta Phys Sin, 2004, 53(9): 3114-3118.
[11] SIRIGIRI J R, SHAPIRO M A, TEMKIN R J. High-power 140-GHz quasioptical gyrotron traveling-wave amplifier [J]. PhysRevtt, 2003, 258302.
[12] 王平. 太赫兹准光回旋器件的三维数值模拟仿真[D]. 成都: 电子科技大学, 2014.
WANG Ping. Three-dimensional numerical simulation of terahertz quasi-optical devices[D]. Chengdu: University of Eelectronic Science and Technology of China, 2014.
编 辑 黄 莘
Research of Terahertz Cyclotron Oscillator Particle Simulation
LIU Da-gang1, WANG Chong-yang1, and LIAOShu-qing2
(1. School of Physical Electronics, University of Electronic Science and Technology of China Chengdu 610054; 2. Institute of Fluid Physics, China Academy of Engineering Physics Mianyang Sichuan 621900)
The calculation errors of particle-in-cell(PIC) method at the conformal boundary are analyzed, especially for the conformal boundary at the THz cyclotron oscillator. The condition of stability and two general treatment methods for the conformal grid are put forward. And the stability and accuracy of these two conformal treatment methods are analyzed. Based on these analysis, an adaptive conformal cell subdivision method is developed. With this method, the problems of the limitation of the conformal grid are solved. The method is implemented on the electromagnetic particle simulation software CHIPIC and is verified by simulating a cylindrical waveguide. Finally, using this method, the THz cyclotron maser with TE26 and the quasi optical cavity cyclotron oscillator with HE06 are simulated successfully.
conformal grid; cut-off frequency; cyclotron oscillator; particle-in-cell simulation; terahertz waves
TN12
A
10.3969/j.issn.1001-0548.2017.02.009
2016-01-30;
2016-07-05
中国工程物理研究院科学技术发展基金(2014B0402057)
刘大刚(1973-),男,博士,副教授,主要从事高功率微波源粒子模拟和太赫兹源模拟等方面的研究.
