香港银行间同业拆借利率的非参数统计分析

黄亚伟��

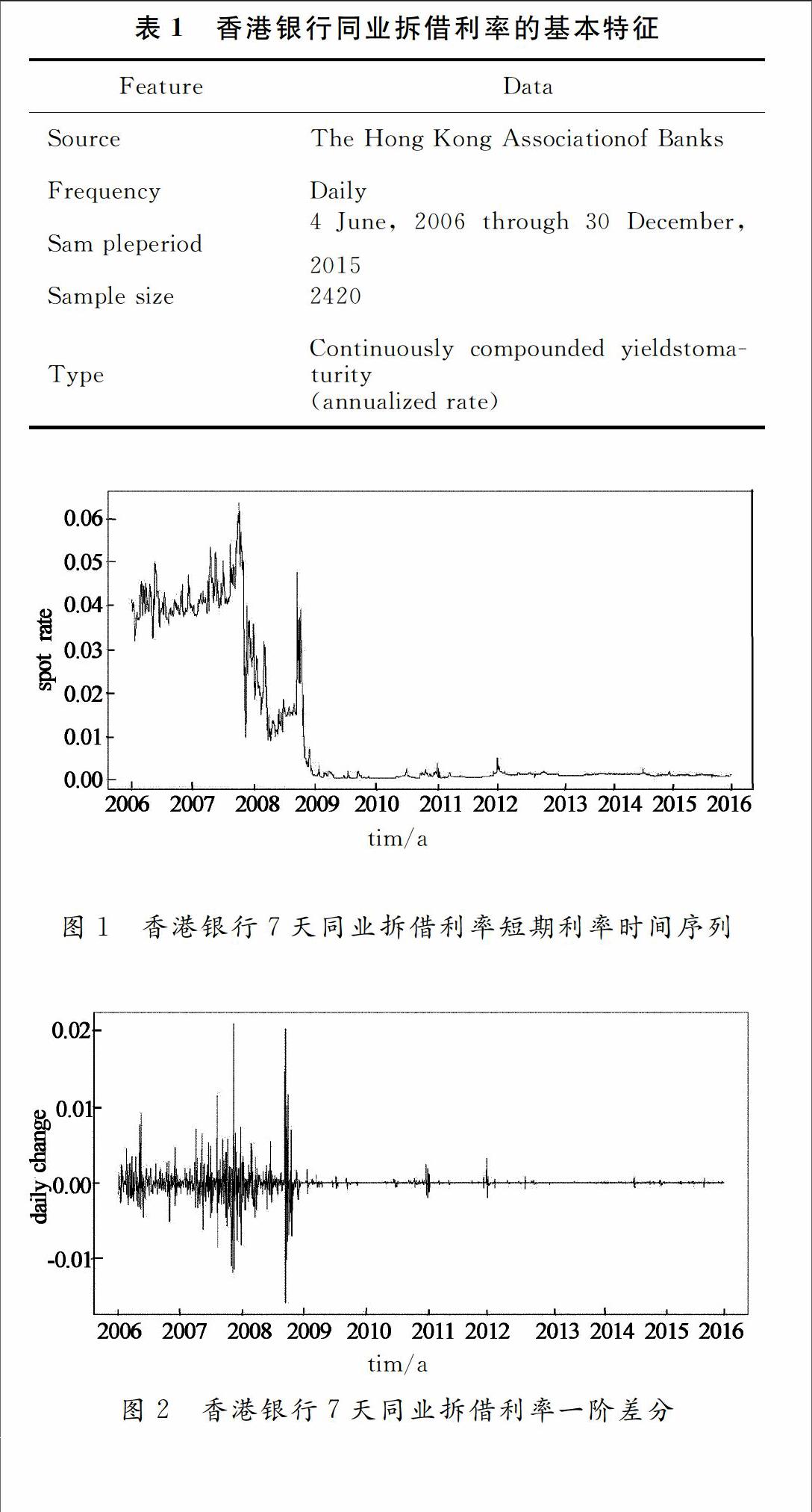
摘要首次利用短期利率模型，分析香港银行同业拆借利率（Hibor），揭示了最近十年内香港银行同业拆借利率的基本特征.初步分析表明，Hibor数据的平稳性不能保证，因此采用了非参数统计方法.利用bandi文章中的方法，给出了函数的漂移项和扩散项的非参数估计，同时还得到了过程的局部时估计.通过实证分析，发现香港银行间同业拆借利率在2006至2015年间，以2009年为界，前后两个时间段的数据表现出不同的特征，样本数据的局部时函数也表现为双峰分布.

关键词香港银行同业拆借利率；非参估计；局部时过程

中图分类号F224.7文献标识码A

1引言

短期利率作为利率结构的基础，是各种金融产品定价的基础依据.学者们在研究短期利率变动过程时，提出了多种利率模型刻画其随机动态特征.

最早提出了一些单因子连续时间扩散模型，如Vaseick[1]，Cox，Ingersolland and Ross（CIR）[2]等模型，并针对美国国债回购市场短期利率进行了实证分析.结果显示美国市场利率存在显著样本均值回复（线性漂移）现象，同时利率波动也受利率水平的影响.AitSahalia[3]对美国7天短期利率实证分析，结论得出带有线性漂移现象的CEV模型不能很好的适用于利率数据，Stanton[4]通过非参数方法估计出短期利率漂移项和扩散项，Jiang and Knight[4]针对有限样本采用了蒙特卡罗模拟方法，都得出样本均值呈现非线性特征.尽管使用参数方法可以得到很好的扩散项估计，但漂移项的估计却是不好的.

在使用非参数方法时，通常需要假设该过程是平稳的.Bandi[6]等人将美国市场利率数据的离散时间间隔化，得出短期利率漂移项和扩散项非参数估计方程.并在研究标量扩散模型时提出了，不需要保证数据平稳性的局部时方法.

以上方法在分析研究短期市场利率中，已经获得了较好的实证结果和相关结论.但是，上述方法主要基于以美国为主的欧美发达国家市场利率.国内的研究者针对中国逐步市场化的短期利率，也进行了一些探索.谢赤和吴雄伟（2002）[7]通过广义矩方法，使用中国货币市场的数据，对Vasicek模型和CIR模型进行了实证检验.分析结果表明，确Vaseick模型与CIR模型相比较，前者能更好地解释中国货币市场的利率变化.洪永森，林海（2006）[8]使用上海证券交易所1996～2004年的7天国债回购利率为样本，通过各种短期利率模型实证分析.研究结果表明，市场存在均值回复现象，非线性漂移对减少模型的设定误差一般不可忽略，引入转换机制和跳跃因子有利于动态模型的拟合效果.刘薇，范龙振（2006）[9]基于CKLS模型对银行间与上海证券交易所债券市场的国债回购利率行为进行比较分析，采用了广义矩估计法，实证结果认为运用CKLS模型模拟银行间市场回归利率变化的过程效果不好，预测能力很弱.整体来看，国内学者针对短期利率模型的研究还相对较少，也还不够深入.

香港银行同业拆借利率是香港银行间互相拆放港元资金所收取的银行利率，作为金融和贷款合同确定的结算利率的基准，是金融市场资金流动性的重要指针.

本文首次利用短期利率模型，初步分析了香港银行同业拆借利率动态变化情况.在平稳性不能保证的情况下本文采用Bandi和Phillips[10]方法，给出利率模型的漂移项和扩散项非参数估计，并进一步采用局部时方法进行分析.

2数据和模型方法

2.1数据

本文使用7天的香港银行同业拆借利率，数据来源于香港金融管理局网站（HKMA）数据库.抽取从2006年1月4日到2015年12月31日的2 420个日常观察数据.由于节假日会对回购时间产生影响，原始数据不能代表真正的7天拆借利率.例如，国庆节和中国的新年等节假日，利率值异常高的，不能作为实际7天拆借利率，所以本文删除了这些数据.表1给出了样本数据的基本特征.

3.1非参数估计结果

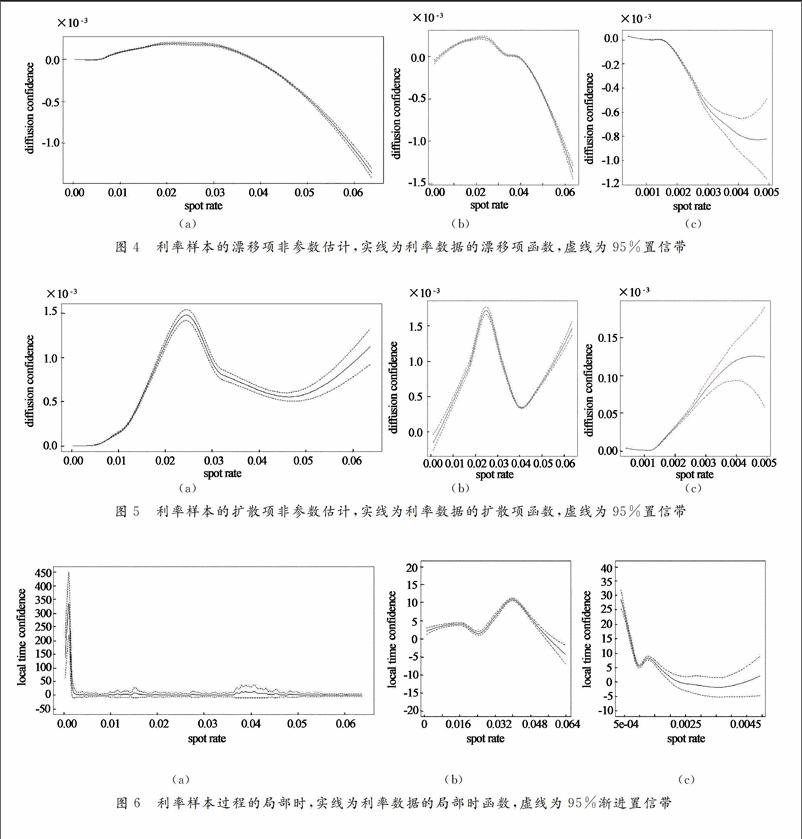
在前面的分析中，漂移和扩散的估计由方程（5）和（6）给出，利用蒙特卡洛模拟方法获得1 000个模拟利率的路径，由此可以得到每一个路径的漂移项和扩散项的估计.

的漂移项和扩散项估计，以及它们的95%置信带曲线.图4是2006年1月至2015年12月（图（4a））整体利率样本的漂移项估计，以及2006年1月至2008年12月（图（4b））、2009年1月至2015年12月（图（4c））利率子样本的漂移项估计.图5是2006年1月至2015年12月（图（5a））的整体利率样本的扩散项估计，以及2006年1月至2008年12月（图（5b））、2009年1月至2015年12月（图（5c））利率子样本的扩散项估计.

在模拟得到的结果中，几乎没有看到高利率，估计项也有相对较大的置区间，可以认为2个估计项都是无偏估计.扩散项估计在低利率水平时，方差也很小，隨着利率增大，方差也随之增大.所以可知，扩散项估计也能够很好的适用于数据.

利率样本过程的局部时，实线为利率数据的局部时函数，虚线为95%渐进置信带

通过Bandi[6]的研究，可以认为短期利率停留在0.1%和4%两处的频率较高.除去这2点及其附近位置，利率停留在其他位置的时间都很短.由此可以认为，利率样本的空间密度函数是双峰的.

数据特征表明，2009年之前短期利率处于高水平状态，随后利率下滑并保持在低水平状态.4结论

本文首次利用短期利率模型，对香港银行间同业拆借利率数据进行分析.抽取从2006年1月4日到2015年12月31日的2 420个日常观察数据.基本结论如下，香港银行间同业拆借利率在2006至2015年间，以2009年为界，前后2个时间段的数据表现出不同的特征.利率样本不能通过ADF检验，数据的稳定性不能保证.基于数据的上述基本特征，本文采用非参数统计方法，分别给出了模型的漂移项和扩散项估计以及它们的95%置信带曲线，最后利用局部时方法分析.结果表明：2009年前短期利率处于高水平，波动较大；2009年后受金融市场影响，利率降低并维持低利率水平，波动减小，处于平稳状态.利率样本动态过程的局部时表现为双峰分布，分析可知单因子利率模型不能很好的适用于利率样本数据，考虑引入状态转换因子.以上研究为今后进一步分析HIBOR市场利率动态特性提供了基础和依据.

参考文献

[1]Vasicek O. An equilibrium characterization of the term structure[J]. Journal of Financial and Quantitative Analysis， 1977， 12（4）：177-188.

[2]Cox J C， Ross S A. A theory of the term structure of interest rates[J]. Econometrica， 1985， 53（2）：385-407.

[3]Aitsahalia Y. Testing continuoustime models of the spot interest rate[J]. Nber Working Papers， 1995， 9（2）：385-426.

[4]Stanton R. A nonparametric model of term structure dynamics and the market price of interest rate risk[J]. The Journal of Finance， 1997， 52（5）：1973-2002.

[5]Theory E. A nonparametric approach to the estimation of diffusion processes，with an application to a shortterm interest rate model[J]. Econometric Theory， 1997， 13（5）：615-645.[6]Bandi F M. Shortterm interest rate dynamics： a spatial approach[J]. Journal of Financial Economics， 2002， 65（1）：73-110.

[7]謝赤， 吴雄伟. 基于Vasicek和CIR模型中的中国货币市场利率行为实证分析[J]. 中国管理科学， 2002， 10（3）：22-25.

[8]洪永淼， 林海. 中国市场利率动态研究——基于短期国债回购利率的实证分析[J]. 经济学， 2006， 5（1）：511-532.

[9]刘薇， 范龙振. 基于CKLS模型的银行间与上交所债券市场国债回购利率行为的比较分析[J]. 预测， 2006， 25（2）：54-58.

[10]Bandi F M， Phillips P C B. Fully nonparametric estimation of scalar diffusion models[J]. Econometrica， 2003， 71（1）：241-283.

[11]Hamilton J D. Time series analysis[M]. Princeton：Princeton University Press，1994.

[12]Scott D W.Multivariate density estimation：theory，practice，and visualization[M]. New York：Wiley，1992.