厚尾随机波动率模型的贝叶斯参数估计及实证研究

黄文礼+张睿轩

摘要针对现有时间序列模型难以刻画参数渐变性的问题，对厚尾随机波动（SV）模型的参数估计方法进行了推广，采用基于贝叶斯的MCMC方法，选取2013年5月～2016年6月这一经历多轮震荡的上证指数作为实证分析对象，构造了基于Gibbs抽样的MCMC过程进行仿真分析.结果显示，以卡方分布作为厚尾参数的先验分布能够有效地描述数据波动的厚尾特征，并且能得到较高精度的参数估计结果.结果表明，厚尾SV模型能有效反映出我国股市尖峰厚尾和波动长期记忆性的特征.

关键词SV模型 ；贝叶斯估计；MCMC方法

中图分类号O218.8文献标识码A

1引言

波动性是金融市场最为重要的特征之一，关于有价证券的收益率波动一直是金融学研究的热点.为了对波动率进行估计，学者们进行过广泛而深入的探索，其中最具代表性的两类模型分别是Engel[1]提出的自回归条件异方差（ARCH）类模型和Taylor[2]提出的随机波动率（SV）模型.但ARCH类模型中条件方差的估计值与过去扰动项直接相关，因此当存在异常观測值时，模型估计出的波动序列不是很稳定.而SV模型假定时变方差是一类不可观测的随机过程，因此其估计的波动序列比ARCH类模型更加稳定.对此，Shephard[3]通过对比两类模型，发现SV模型比ARCH模型能更好地描述金融数据的特性，特别是对2个模型的预测的均方误差的比较发现，SV模型比ARCH模型具有更好的预测能力，尤其是对长期波动性的预测[4].

但是，由于SV模型自身的复杂性，模型的似然函数解析式与无条件矩的解析形式往往难以获得，无法进行极大似然估计，故如何对SV模型进行参数估计就是一个具有现实意义的问题.对此，Metropolis提出了马尔科夫蒙特卡洛（MCMC）方法，Hasting[5]在此基础上提出了MetropolisHasting算法，Geman[5]提出了Gibbs抽样，这两种算法因其灵活性和计算机技术的发展，使得针对复杂模型及其后验分布的精确估计成为可能.除了MCMC方法，国外学者对SV模型的估计方法进行了大量研究，并取得了丰富的成果：Harvey[5]等人的伪极大似然估计，Anderson，Chung[5]的有效矩估计， Dimitrakopoulos Stefano[6]针对时变参数SV（TVPSV）模型提出的一种半参数贝叶斯估计方法，Milan Mrázek[7]等人基于非线性最小二乘法对分数维SV模型参数估计精确度的校准.在众多估计方法中，蒙特卡罗随机模拟相对于其他方法，效率较高，易于编程实现.本文即选用基于贝叶斯的MCMC方法对SV模型进行参数估计.

由于许多金融时间序列的无条件分布与标准正态分布相比，会呈现出较大的峰度和更厚的尾部，因此为了将基本的SV模型扩展到较一般的形式，经过学者们多年的研究，SV类模型已经发展出了离散和连续两类的众多扩展模型.比如，Geweke[7]对模型进行贝叶斯分析时提出了厚尾SV模型，即将标准SV模型中观测方程的随机误差项设定为具有厚尾特征的概率分布如t分布、GED分布等，从而可以更好地描述金融时间序列的尖峰厚尾特征.Bredit[8]针对金融波动序列的长记忆性提出了长记忆随机波动模型（LMSV），Chib[5]将跳跃过程引入到了SV模型中，提出了跳跃SV模型，并提供了一种快速有效的估计模型参数的MCMC算法，以此来解决如何反映金融市场中的突发事件和较大波动的问题.

经济数学第 34卷第1期

黄文礼等：厚尾随机波动率模型的贝叶斯参数估计及实证研究

近年来，国内学者对SV模型进行了大量研讨，这其中包括：刘凤芹和吴喜之[9]利用一种改进的MCMC方法估计了SV模型，并对上证指数进行了波动性分析；朱慧明[10]在研究沪深300股指期货数据时，考虑到期货市场与现货市场之间存在双向波动溢出效应以及仿真交易与实盘交易在期货与现货联动性、交易策略等方面存在的差异，建立了一个多变量厚尾SV模型，并借助MCMC方法实现了模型的参数估计.于冉春[11]分别选用标准SV模型和厚尾SV模型对美国标普500指数进行了实证分析，得出厚尾SV模型更能够准确描述标普指数波动具有长期记忆性的特征.而吴鑫育、马超群[12]等以上证指数和深证成指为例，提出极大似然方法估计了4种不同收益率分布假定的SV模型，通过比较认为具有偏学生t分布假定的SVSKt模型能够更好地描述中国股票市场的波动性.在研究中发现，我国股市呈现出许多不同于传统研究中波动的典型特征，比如反杠杆效应，即股票价格运行未来价格波动呈现正相关关系，特别是2015下半年和2016年年初，整个股市出现了罕见的大幅波动.而对于具有以上新型特征的中国股市，有关厚尾SV模型是否还能有效刻画出我国资本市场波动性的相关研究还相对缺乏.本文考虑到金融时间序列普遍存在的尖峰厚尾性，为了验证SV模型对现阶段我国股市的拟合效果，拟进行基于MCMC仿真的厚尾SV模型的贝叶斯参数估计，研究以上证综指为代表的金融时间序列的波动特征.

2厚尾SV模型结构

重复以上步骤进行N次迭代，直到Markov链达到平稳状态.在Gibbs抽样的初始阶段，参数的初始值设定对随机数的生产有较大的影响，此时Markov链是非平稳的，所以在估计模型参数时，通常去掉最初的M个非随机数，对剩下的NM个抽样数据进行模型参数的后验分布统计推断.

4估计结果和分析

4.1样本数据和统计特征

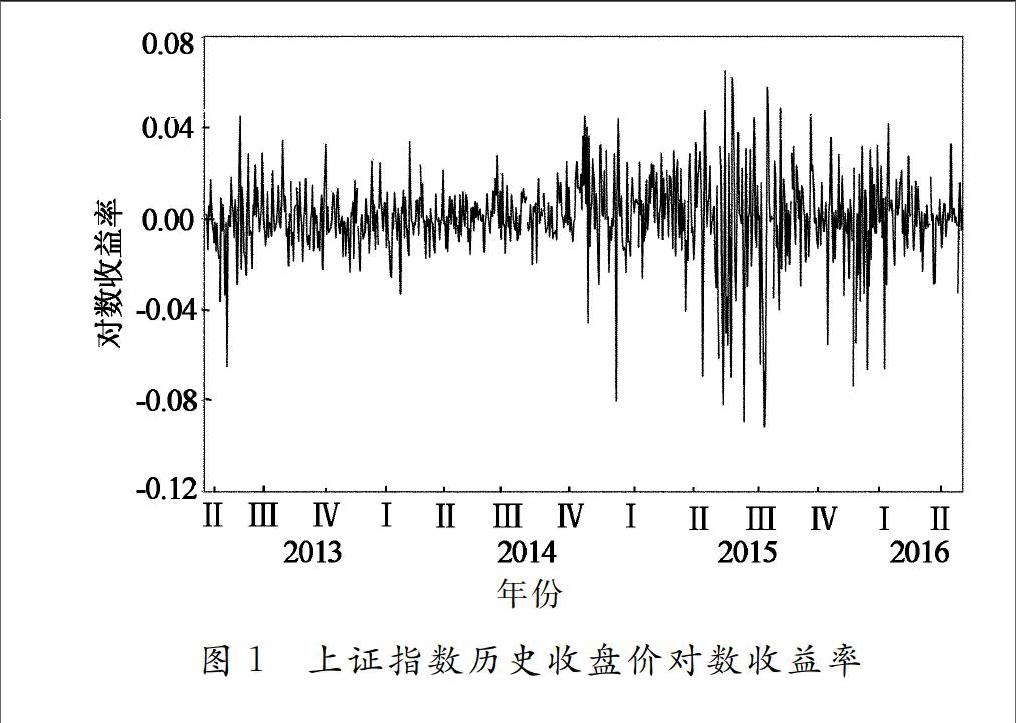
2015年开始，中国股市再次表现强劲，然而受多种因素影响，上证综指又从2015年6月的5 300多点跌至2016年5月的2 800多点，期间又经历了2016年年初的熔断机制事件，短短一年多时间，中国股市就经历了史无前例的大牛市和超级熊市，股票价格波动剧烈，这表明我国股市还存在非常多的问题.因此本文使用的数据包括2013年5月～2016年6月的上证指数历史收盘价，样本容量为752，涵盖了本轮牛市之前、期间、之后的数据，以分析中国股市的波动特征.收益率的计算本文均采用对数收益率方法，并绘制出对数收益率的时序图和直方图，见图1.同时，利用QQ图对上证指数的统计特征进行分析（见图2）.

通过分析，发现上证指数实际数据的峰度比正态分布数据的峰度要高，腰部较瘦，尾部较厚，并且直方图并不是完全对称的，而是略有偏斜.从Q-Q图中可以很明显的看出上证指数和指数的收益率分布在收益和损失两端均偏离直线，因而表现出明显的厚尾特征，也就是出现异常值的频率比正态分布的要高.因此再次验证了中国股市尖峰厚尾特性.

4.2参数估计结果和分析

本文使用MCMC仿真方法对厚尾SV模型进行贝叶斯参数估计，首先对每个参数进行 1 000次迭代，进行退火，以保证参数的收敛性.然后舍弃原来的迭代，再进行10 000次的迭代对模型进行模拟仿真的过程.图3给出了厚尾SV模型参数相应的后验分布密度函数仿真结果，参数估计结果见表1.

由图3可知，对于厚尾SV模型的参数，其后验分布密度图基本上是对称的，说明这些参数的贝叶斯估计值与真实值非常接近，误差很小.但是对于参数τ，其后验密度函数都呈现出右偏趋势，说明这些参数的样本中存在一些偏大的异常点，使得它们的贝叶斯估计值比真实值要大，因此参数τ可能会被高估.同样得，参数φ的后验密度函数呈偏左趋势，说明参数中存在一些偏小的异常点，使得它们的贝叶斯估计值比真实值要小，故参数φ可能会被低估.

虽然厚尾SV模型的某些参数的贝叶斯估计值可能会偏高或偏低，但是整体看来，模型各个参数的后验分布密度都具有非常明显的单峰特征，说明利用后验均值对模型参数进行估计的误差是非常小的.因此，综合对厚尾SV模型参数的样本轨迹图以及后验分布密度图的分析可知：对厚尾SV模型参数进行贝叶斯估计是合理的，并且估计结果是有效的.

结合模型参数的贝叶斯估计情况，首先可以看出SVT模型参数的估计结果是比较精确的，各参数的MCMC误差相对于标准差都要小很多，再一次验证了对厚尾SV模型参数进行贝叶斯估计的合理性.并且在程序运行的时间也较短，表明算法的精确度和效率是比较好的.同时可以得到以下结论：厚尾SV模型的厚尾成分参数ω估计值为16.1，且MC误差为0.239 7，表明上证综指的收益率不服从正态分布，具有明显的厚尾特征，此结论与前面对QQ图的分析结果是一致的；厚尾SV模型的波动持续性值φ为0.860 4，这说明上证指数具有较为明显的波动持续性，这也与在实际生活中的感受相吻合：样本数据涵盖了2013年～2016年的上证指数收益率，期间整个资本市场经历了多轮较大起伏的波动，且一个大的波动之后往往跟着另一个波动.SVT模型在模拟波动持续性这一波动特点上的具有良好的拟合效果.

5总结

本文针对厚尾SV模型进行了贝叶斯分析，分析了模型的结构特征，对模型的参数进行了贝叶斯统计推断，设计了模型参数估计的Gibbs的抽样算法.在对中国股市的波动性进行实证研究时，选取了近一轮股市波动前中后三个不同阶段的数据，以更加全面地了解我国股市的波动特征，并以此为例来检验厚尾SV模型在新兴资本市场当中的拟合效果.结合对上证指数的统计分析以及MCMC抽样方法中参数的样本轨迹收敛性，本文认为，在股市经历较大幅度波动时，厚尾SV模型仍然能够比较准确地描述中国股市的波动性特征.

参考文献

[1]Engel R F. Automatic conditional heteroscedasticity with estimation of the variance of the united kingdom inflation [J].Econometrica， 1982， 50（4）：987-1007.

[2]Taylor S J. Modelling financial time series [M].Hoboken： John Wiley，1986.

[3]Harvey A， Shephard N. Estimation of an asymmetryic stochastic volatility model for asset returns [J].Journal of Business and Economic Statistics，1996，14（4）：429-434.

[4]郝利亞， 朱慧明. 贝叶斯金融随机波动模型及应用[M].北京：经济管理出版社， 2015.

[5]于冉春. 基于MCMC贝叶斯方法的随机波动率模型实证研究[D].上海：上海师范大学商学院. 2014.

[6]Dimitrakopoulos S. Semiparametric Bayesian inference for timevarying parameter regression modelswith stochastic volatility [J].Economics Letters. 2017，150（1）：10-14.

[7]Milan M， Jan P， Tomá S. Oncalibration of stochastic and fractional stochastic volatility models [J].European Journal of Operational Research. 2016，254（3）：1036-1046.

[8]黄超. 基于贝叶斯跳跃厚尾随机波动模型的中国股市波动性研究[D]. 长沙：湖南大学工商管理学院. 2010.

[9]Breidt F J， Crato N， Lima P. The detection andestimation of long memory in stochastic volatility[J].Journal of Econometrics，1998，83（1）：325-348.

[10]刘凤芹，吴喜之. 随机波动模型参数估计的新算法及其在上海股市的实证[J].系统工程理论与实践， 2006， 26（4）：27-31.

[11]朱慧明， 李锋， 杨锦明. 基于MCMC模拟的贝叶斯厚尾金融随机波动模型分析[J].运筹与管理. 2007， 16（4）：111-115.

[12]吴鑫育，马超群，汪寿阳. 随机波动率模型的参数估计及对中国股市的实证[J].系统工程理论与实践. 2014，34（1）：35-44.

[13]Kim S，Shephard C.Stochastic volatility：likelihood inference and comparison with ARCH models[J].Review of Economics Studies， 1998，224（65）：361-393.

[14]Jun，Yu. Forecasing volatility in the New Zealand stock market[J].Journal of Finance Economics， 2002，12（3）：193-202.

[15]Meyer R， Jun Y. BUGS for a Bayesian analysisof stochastic volatility models[J].Econometrics Journal， 2000，3（2）：198-215.