对重尾分布及现象的探讨

叶南吉

摘 要 在现实生活中，重尾现象随处可见。本文针对重尾的概念、现象及一些风险测量方法如VaR、EVT进行了介绍，希望可以引起人们对极端损失的关注和更深入的研究。

关键词 尾部分布；重尾现象；风险价值度VaR

一、重尾的概念及现象

1.何为重尾

重尾也称长尾、肥尾。概率统计中，重尾分布是一种机率分布的模型，其特点是尾部比指数分布还要厚。在金融领域，我们通常以投资证券的收益作为横坐标研究收益的概率分布，因而右边尾部（损失）的分布会比较受到重视，但左边尾部比较厚，或是两边尾部都很厚的狀況，也会被认为是一种重尾分布。

2.重尾现象

自然界中的重尾現象表现在少量个体占用大量资源，比如空气中氮气与氧气的比例约为78：21；人脑中水与其他物质之比例大概是80：20……。

在金融市场上，重尾带来的灾难性后果也无处不在。它暗喻着客观世界的极端波动性，指那些发生概率虽低，但一旦发生就会产生毁灭性冲击的事件，像飓风、火灾、重大车祸等。放眼历史，2011年3月11日发生在日本的里氏9级大地震导致日经指数在一周内下跌12.85%；同年7月23日，甬温线动车追尾事件导致了次日沪市暴跌82.04点；最令人难忘的应该是08年美国次贷危机，其辐射范围之广，影响之恶劣令人唏嘘。凡次种种，都在告诫各个部门企业乃至国家加强对未知事物的风险管理。

二、重尾分布在概率论中的解释

在概率论中，取正值的连续随机变量的k阶原点矩定义为 ，这个积分结果依赖于密度函数f（x）和k，当然也可能积分不存在，如果在x很大时密度函数也很大，就有可能会导致积分不收敛。对于一个随机变量，如果任意的正数阶原点矩存在，那么说明分布的尾部很轻，而正数阶矩存在最高阶数（或不存在正数阶矩），则说明分布的尾部很厚。

19世纪末期，意大利经济学家维弗雷多·帕累托认为，贫与富的存在，既是经济问题，也有政治原因。帕累托在研究英国人的收入分配问题时发现，绝大部分社会财富最终总会流向少数人群；他还发现，某一部分人口占总人口的比例，与这一部分人所拥有的财富的份额具有比较确定的计量经济关系。进一步的研究证实，这种不平衡模式可以重复出现，甚至可以预测。经济学把这一社会财富的分布状态，称为“帕累托分布”。Pareto型随机变量属于常见的重尾分布族，包括Pareto分布、Burr分布和Frechet分布等，定义如下：

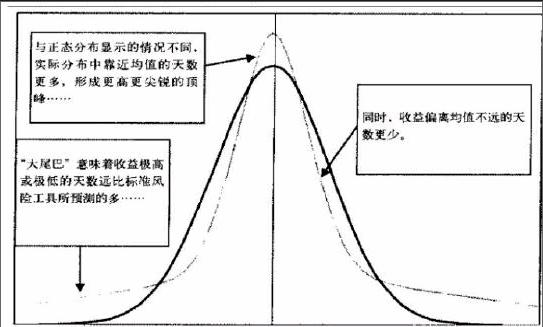
尖峰厚尾是我们经常遇到的一种分布状态，偏度和峰度都是描述分布形状的特征数。偏度对应随机变量的三阶矩，是描述分布偏离对称性程度的一个特征数；而峰度则对应着四阶矩，是相对于正态分布而言的超出量。对于一个标准正态分布而言，它的偏度skew=0，峰度kurtosis=3，因此当我们说一个分布有厚尾时也就表明它的峰度值大于3。如下图很好地对比了正态分布与一个尖峰厚尾分布。

三、衡量尾部风险常用方法

1.VaR的优缺点分析

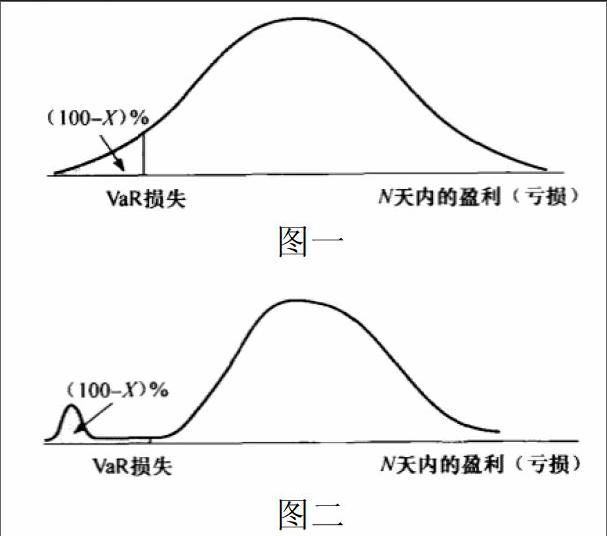
在金融领域中，金融机构常常用在险价值（value at risk ， VaR）来度量市场中的风险程度，VaR（V）是两个参数（时间展望期N和置信度X%）的函数，可以表达成：我有X%的把握，在今后的N天内损失不会超过V。这看似是一个非常有效的风险测量方式，但它并不是一个一致的风险测量方式，因为它并不能满足风险的次可加性，即两个投资组合的VaR之和大于将两者合并之后组成的新的投资组合的VaR。而次可加性是任何一个风险度量必须满足的重要性质，它刻画了现代投资组合理论中的风险分散化原则，是资产组合决策问题的一个基本条件。如下图中两者都表示投资组合价值变化概率分布，且图二为图一的变形，我们可以观察到，尽管VaR值相同，但图二的潜在损失明显大于图一，直接使用VaR判断很可能使得交易员选择图二中分布特性的投资组合，带来更高的风险。

2.VaR基础上的改进

基于传统方法在估计VaR时存在的缺陷，近年发展起来了极值理论（EVT），该理论只对资产收益的尾部数据进行分析而不考虑整体回报率，从而能更加直接地描述小概率的极端数据并进行模拟，考虑到了现实中可能发生的极端风险又可以规避一定的模型误差，对传统VaR的不足作出了一定的完善。

四、结论与展望

证券资产投资收益、保险索赔及许多人类行为都表现出重尾特征，如何准确估计重尾指数一直是我们研究的重点。人们总是对资产收益率的大起大落的情况更为关注，如股票的暴涨和暴跌就表现在股票极端收益率上，而这些都是由收益率分布的尾部特征所决定。又如对保险公司来说，对可能发生的极端事件而导致的巨额索赔需要进行大量数据的分析整理，去准确合理地定出保费，便于有效管理风险。因此，每一个风险管理者都需要做好对尾部风险的防范及对冲，在充满不确定性的未知世界中把握住自己前进的方向。

参考文献：

[1]陈思思.关于保险与金融中重尾现象的若干研究，浙江工商大学，2012

[2]邢红卫.重尾现象、重尾分布与重尾指数估计，山西大学，2010

[3]John C.Hull，Options，Futures And Other Derivatives（Eighth

Edition），2012