不规则图形的面积求稿

刘烨锟

在生活中，我们常常会遇到各种各样的不规则图形，有时需要测量或计算它们的面积，但由于图形不规则，很难用简单的数学公式求解。

本文通过一个典型案例初步探讨了如何求解不规则图形的面积。

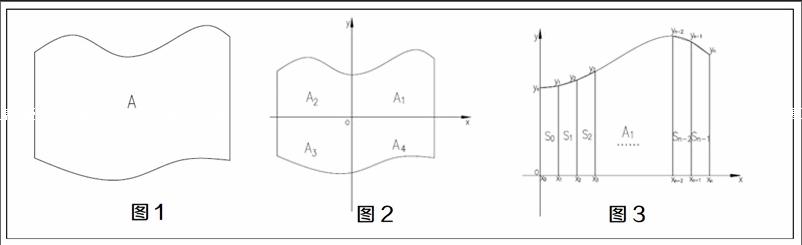
例题：计算图1所示的图形面积A。

分析：面对这种图形，可先在靠近中心的位置建立坐标系，将其分成四塊不规则的图形A₁，A₂，A₃，A₄，分别求解其面积，再将四块面积相加就可以得到整块不规则图形的面积，如图2。

现以其中A₁的面积求解为例，探讨如何求解A的面积。

先将图形A₁在X轴方向上的距离L分成n等分，每等分的坐标分别为X₁，X₂，X₃……X_n，其在图形边缘对应的y值分别为y₁，y₂，y₃……y_n，如图3。

将每一等分内的区域视作一个梯形，梯形的面积近似等于该区域的面积。如等分n越大，其计算所得面积越接近A₁的实际面积。设每个梯形的面积为Si。

Si=（y_i+y_i+1）×（X_i+1-X_i）/2

其中，（X_i+1-X_i）=L/n

因此：Si=（y_I+y_i+1）×L/（2n）此区域的面积A₁=S₀+S₁+……S_n-1

代入S_i即为：

A₁=（y₀+y₁）×L/（2n）+（y₁+y₂）×L//（2n）+……+（y_n-1+y_n）×L/（2n）

=（y₀+2y₁+2y₂+2y₃+……+2y_n-1+y_n）×L/（2n）

在区域的边界上取若干个点，获得其坐标（x₀，y₀），（x₁，y₁）……（x_n，y_n），将其数值代人上述公式中，即可大致求得不规则图形A₁的面积。取点越密集，即均分的等分越多，n越大，求得的面积越精确。

按照上述方法求出其他区域的面积，相加即可求得整个不规则图形的大致总面积。