布谷鸟算法的收敛性分析及其改进

陆伟峰

(苏州工业园区服务外包职业学院 人文艺术学院，江苏 苏州 215123)

布谷鸟算法的收敛性分析及其改进

陆伟峰

(苏州工业园区服务外包职业学院 人文艺术学院，江苏 苏州 215123)

使用差分方程方法分析了布谷鸟搜索算法收敛的条件，分析其寻优的原理。针对算法后期收敛速度降低，容易陷入局部最优值的问题，使用局部随机搜索技术提出了改进的布谷鸟搜索算法。仿真实验结果表明，改进的算法有效提高了基本布谷鸟算法的收敛速度和精度。

布谷鸟搜索算法；差分方程；收敛性分析；局部随机搜索

布谷鸟搜索算法(cuckoo search，CS)是由剑桥大学的Yang等[1]提出的一种群知能优化算法。与蚁群算法(ACO)、粒子群算法(PSO)、蜂群算法(ABC)等相比，CS算法具有参数少、鲁棒性强和不易陷入局部最优等优点。目前，CS算法已成功应用于工程优化、洪水预测、流水线调度、人脸识别、语音识别、神经网络训练等领域[2]。为提高算法的收敛速度与精度，众多学者进行了研究，引入了逐维改进策略、基于Powell局部搜索策略[3]，各种自适应方法[4-6]、闭环控制策略[7]、差分进化方法[8]、基于小生境技术的逐步档案缩减[9]、动态惯性权重[10]等各种方法提高了算法的性能。CS算法的收敛性分析相对较少，周欢等[10]提出了具有动态惯性权重的布谷鸟搜索算法，并用差分方程进行了收敛性分析，王凡等[11]应用马尔科夫模型证明了CS算法的收敛性。然而，CS算法的微观机理依然不是很明确，算法的收敛性不能得到保证；特别是在后期，算法的开发能力不足，收敛速度降低，易陷入局部最优值。本文分析了CS算法的收敛性条件，并提出了一种局部随机搜索的改进方法。测试结果表明，改进算法具有较快的收敛速度和较高的精度。

1 基本布谷鸟算法

布谷鸟搜索算法(CS)模拟了布谷鸟的巢寄生殖行为与莱维飞行机制(Levy flight)。巢寄生性是指布谷鸟本身没有孵化行为，总是把卵产在其他相近鸟类的巢里，其他鸟类为其孵化卵，或者以一定的概率发现而丢弃卵。莱维飞行是指其飞行是一类非高斯随机过程，其平稳增量服从Levy稳定分布。飞行中步长较小的短距离行走于偶尔的较大步长的长距离行走相互交替。短距离行走有利于局部搜索，偶尔的长距离行走则易于跳出局部最优点，加强全局搜索。

布谷鸟算法设定了三条理想规则[1]：①每只布谷鸟每次只生产一个卵，并随机选择寄生巢来孵化；②在寻找巢的过程中，卵最好的鸟巢将会被保留到下一代；③鸟巢的数量是固定的，并且设鸟巢中外来卵被发现的概率为，如果发现外来卵，则鸟窝主人重新建立一个鸟窝。

基本CS算法的具体步骤如下[3，12]：

5) 评价并保留最好的解Xbest。

6) 判断是否达到终止条件，如果达到，算法终止；否则转步骤2)。

2 基本CS算法的收敛性分析

在基本CS算法中，假设鸟巢的最优位置Xbest保持不变，并记则算法性能主要受随机因子at影响。在不考虑被发现的情况下，CS算法可以表示为一个一阶线性差分方程，得到以下收敛性条件。

定理1 基本CS算法收敛的充要条件是

证明 由式(1)和式(3)得一阶线性差分方程

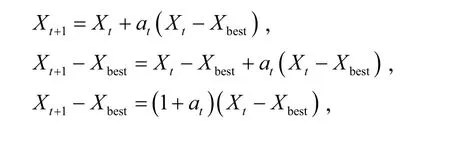
由式(4)得到

图1 满足收敛条件下的进化情况

图2 不满足收敛条件下的进化情况

证明 当t＞t0时，有-2＜at＜0，-1＜1+at＜1，由定理1，此时Xt收敛于Xbest。

同样取Xbest=20，X1=-5，运行50次验证定理2的有效性。图3中at为(-2，0)上均匀分布的随机数，此时Xt收敛于Xbest=20；而在图4中at为(0，1)上的随机数，Xt发散。

定理2 基本CS算法收敛的一个充分条件是对于某一整数t0＞0，当t＞t0时，有-2＜at＜0。

图3 at～U[-2，0]上的进化曲线

图4 at～U[0，1]上的进化曲线

基本CS算法的寻优过程可以用勘探(exploration)和开发(exploitation)两个过程进行描述[13]。勘探是指在为搜索过的区域进行搜索。开发是指在当前最优位置附近进行搜索。通过莱维飞行算法在勘探(at2＜at＜0)与开发(at≤-2或者at≥0)之间切换，辅以“偏好随机游动”过程实现整体的寻优。

3 改进的CS算法

根据CS算法的更新公式Xt+1=Xt+at(Xt-Xbest)，每个卵寻优的动力来自于莱维飞行部分at(Xt-Xbest)。一方面，在寻优后期，由于Xt-Xbest→0，算法的开发能力急剧减弱，收敛速度降低；另一方面，在满足收敛的条件下，算法收敛于当前最优位置Xbest，但是Xbest并不一定是全局最优位置，从而陷入局部最优。

针对以上问题，本研究提出一种基于局部随机搜索技术的改进CS算法(local random search CS，LRS-CS)，其基本思想是：一部分布谷鸟(i≤n0)按原有算法，通过莱维飞行搜索。另一部分布谷鸟(i＞n0)通过在当前最优巢Xbest前引入随机因子，并令at为(-2，0)上均匀分布的随机数。通过加强局部随机搜索，提高算法性能，即将式(1)改为

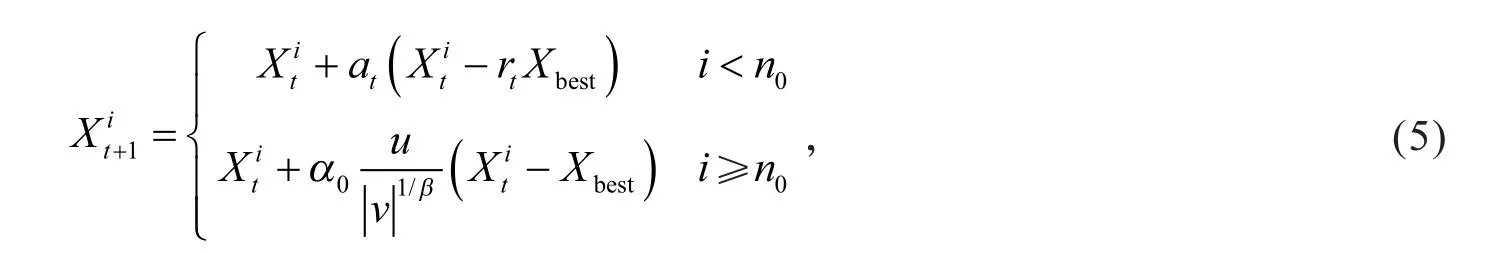
使得算法以一定的概率向Xbest邻域中的点而不是Xbest收敛，扩大寻优的区域。同时，克服了算法后期Xt-Xbest→0而产生的开发动力不足的问题，加快收敛速度。

4 仿真实验

为测试本研究提出的改进CS算法的效果，选取文献[14]、文献[15]中的9个标准测试函数进行仿真实验，见表1。其中F1-F4为单峰值函数，F5-F9为多峰值函数。

设定改进CS算法的参数an'服从(-2，0)之间的均匀分布，。为考察算法的性能，算法进化5 000代，每个函数分别取10、20、30维独立运行30次，计算平均适应度(Mean)、最优适应度(Best)、最差适应度(Worst)、标准差(SD)等指标。实验结果如表2所示。与基本CS算法比较，不论对单峰值还是多峰值函数，改进的CS算法大幅提高了寻优的精度。对于F1、F2、F4、F5、F9都能找到最优值。同时在问题维数增加时，改进CS算法的求解精度变化不大。

表1 测试函数

表2 两种算法的试验结果比较

图5是采用两种算法的典型进化曲线图(适应度取对数log10)。由图5可以发现，改进的CS算法较基本CS算法的收敛速度也有很大提高。

图5 F1—F9的进化曲线

综合比较，改进的CS算法收敛速度快、精度高，对于不同维数的问题，适应能力强，具有良好的鲁棒性。

5 结论

使用差分方程方法证明了基本CS算法收敛的条件。针对基本CS算法后期收敛速度慢、易陷入局部最优值的问题，提出了基于局部随机搜索技术的改进CS算法。实验结果表明，与基本CS算法相比，改进的算法具有更高的收敛精度与更快的收敛速度，并具有良好的鲁棒性，对问题维数不太敏感。

[1] 兰少峰，刘升.布谷鸟搜索算法研究综述[J].计算机工程与设计，2015，36(4)：1063-1067.

[2] FISTER I，YANG X S，FISTER D，et al.Cuckoo search：a brief literature review[J].Physics，2014，516(2)：49-62.

[3] 马卫，孙正兴，李俊楼.基于Powell局部搜索策略的全局优化布谷鸟算法[J].计算机应用研究，2015，32(6)：1667-1675.

[4] 江浩，阮奇.基于变尺度法和自适应步长的布谷鸟搜索算法[J].计算机技术与发展，2015，25(10)：38-43.

[5] 郑洪清，周永权.一种自适应步长布谷鸟搜索算法[J].计算机工程与应用，2013，49(10)：68-71.

[6] 贺淼，阮奇，郑晓桂，等.自适应布谷鸟搜索算法[J].计算机与应用化学，2014，31(8)：961-968.

[7] 张永韡，汪镭，吴启迪.动态适应布谷鸟搜索算法[J].控制与决策，2014，29(4)：617-622.

[8] 肖辉辉，段艳明.基于差分进化的布谷鸟搜索算法[J].计算机应用，2014，34(6)：1631-1635，1640.

[9] 贺兴时，李娜，杨新社，等.多目标布谷鸟搜索算法[J].系统仿真学报，2015，27(4)：731-737.

[10] 周欢，李煜.具有动态惯性权重的布谷鸟搜索算法[J].智能系统学报，2015，10(4)：645-651.

[11] 王凡，贺兴时，王燕，等.基于CS算法的Markov模型及收敛性分析[J].计算机工程，2012，38(11)：180-182，185.

[12] 王李进，尹义龙，钟一文.逐维改进的布谷鸟搜索算法[J].软件学报，2013，24(11)：2687-2698.

[13] SCHMITT M，WANKA R. Particle swarm optimization almost surely finds local optima[C]//Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation，ACM，2013：1629-1636.

[14] LIANG J J，QIN A K，BASKAR S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation，2006，10(3)：281-295.

(责任编辑：李 华)

The Convergence Analysis of the Cuckoo Search Algorithm and Its Improvement

LU Weifeng

(School of Humanities and Arts，Suzhou Industrial Park Institute of Services Outsourcing，Suzhou 215123，China)

This paper analyzes the convergence of cuckoo search algorithm and its searching principle with the help of the differential equation method. As the algorithm convergence speed rapidly reduces at the late period and it’s easy to fall into the local optimal value of the problem，an improved CS algorithm is proposed using local random search method. The simulation results show that the improved algorithm can effectively increase the convergence speed and accuracy of basic CS algorithm.

cuckoo search algorithm；differential equation；convergence analysis；local random searching

G203

A

1008-5475(2017)01-0010-06

10.16219/j.cnki.szxbzk.2017.01.003

2016-12-02；

2016-12-18

陆伟峰(1978-)，男，江苏太仓人，讲师，硕士，主要从事智能计算、智能控制、数学教育研究。

陆伟峰.布谷鸟算法的收敛性分析及其改进[J].苏州市职业大学学报，2017，28(1)：10-15.