城市集中供热系统热流量优化分配研究

杨伟东，徐宵伟，贾鹏飞，马媛媛，何晓东

（河北工业大学 机械工程学院，天津 300130）

城市集中供热系统热流量优化分配研究

杨伟东，徐宵伟，贾鹏飞，马媛媛，何晓东

（河北工业大学 机械工程学院，天津 300130）

集中供热系统流量的质调节和量调节之间耦合关系是制约其控制性能的关键问题，供热系统也存在滞后性、时变性以及参数的不确定性等因素.针对以上问题，采用一种改进的专家模糊PID控制方法对质量并调供热方式进行解耦控制.为了提高模糊PID控制器的精度，采用专家系统对模糊控制的量化因子进行优化.最后对改进后的专家模糊PID控制器进行了仿真验证，结果表明改进的专家模糊PID控制器较常规的模糊PID控制器不仅能实现供热网管质量并调控制的解耦，还具有更好的动态特性.

集中供热；解耦控制；专家控制；模糊PID控制

0 引言

热网流量的控制是集中供热的重要环节，热网流量分配的好坏直接影响到城市供热工作的质量.在热网流量控制过程中，根据天气地域等特点，要求保证供给热用户的热量维持热用户的室内温度在一定范围内变化，但集中供热系统具有多变量、非线性、强耦合、大滞后及时变性等特点，难以根据其特征构建精确的数学模型，从而往往导致控制效果不理想[1].所以针对这些特点，对现有的控制方法深入分析和研究具有十分重要的意义.

解耦技术由传统解耦向智能解耦逐步发展，但目前在集中供热系统中应用很少.文献 [2]中介绍了现代频域法，它将系统传递函数进行分解实现其对角化或对角优势化以实现解耦目的，但不能保证系统精度和鲁棒性.文献 [3]中介绍了多变量PID自适应解耦控制器，但PID控制器受现场环境影响大，且不适合在非线性系统中应用.文献 [4]中采用基于后推法的非线性多变量耦合系统的逼近干扰解耦法，既简化了系统结构又减少自适应参数，但只能控制单一的非线性函数.文献 [5]中采用粒子群算法优化PID神经元网络初始权值，达到提高控制器的收敛速度和精度的目的，但容易早熟收敛且局部寻优能力较差.文献 [6]中采用干扰观测器的自适应模糊跟踪控制方法解决非线性多变量耦合，达到提高不确定性条件下闭环系统的抗干扰能力和稳定性，但通用性不强.

本文采用改进的专家模糊PID控制器对热网的流量进行控制，将模糊PID控制器对质量并调的供热系统进行解耦控制，采用专家系统对模糊PID控制器的相关参数进行调整.该控制器能够提高系统的鲁棒性以及自适应性，对集中供热系统的控制质量的提高及能源消耗的减少有较显著效果，并且具有很强的通用性.

1 城市集中供热管网的控制原理

集中供热系统是根据实际热网工况和管网条件，采用换热站进行连接完成从供热一次网到二次网的热量交换，通过将热媒加以调节和转换，向热用户系统分配热量以满足用户的需求，如图1所示.

图1 集中供热系统管网运行原理图Fig.1 Operation principle diagram of pipe network in the central heating system

在集中供热系统中，热水管网分为一次网和二次网.一次网将热源产生的高温水经换热器将热量传递给二次网，完成热传递后返回热源重新加热.二次网是将换热器得到的热量在热用户处释放后再返回到换热器.其中的量调节是通过改变循环泵的频率而改变二次网的流量，以达到控制进入热用户的热量.质调节是通过改变一次网电动调节阀而改变进入换热器的高温水的量，以达到控制二次网的供水温度[7].

质调节和量调节之间存在着耦合关系，因此需对集中供热系统的流量进行解耦，为流量优化分配提供精确的对象模型，在质调节和量调节控制过程中采用改进的专家模糊PID控制器进行并联控制，以达到集中供热管网中流量的双闭环控制，最终实现流量优化分配.

1.1 供热管网质量并调耦合模型的建立

图2 集中供热质量并调耦合模型原理图Fig.2 Principle diagram of the collaborative control mode between qualitative regulation and quantitative regulation in the central heating system

图2为集中供热质量并调耦合模型原理图，该耦合模型的数据采样是取自天津市滨海新区某热力公司.采样时通过固定其中1个参数，改变另一个参数得出单个调节方法对系统的影响.先改变一次网电动调节阀的开度，保持变频器频率不变，记录二次网供水温度、回水温度和流量的实时数据值；再改变二次网循环泵变频器频率，记录二次网供水温度、回水温度和流量的实时数据值.通过机理建模和试验建模相结合的方法，建立供热过程的质量并调数学模型如下[8].

热网质量并调流量的控制主通道为

两个耦合通道的模型采用与主通道相同的数据进行建模，分析如下：

1）以二次网循环泵变频器的输出频率为控制量，二次网供水温度为被控量的耦合模型，采用二阶加零点模型：

2）以一次网电动电磁阀的开度为控制量，二次网内的流量为被控量的耦合模型，采用一阶加滞后模型：

完整的热网流量控制耦合模型为：

对于所得到的热网流量质量并调耦合模型，采用改进的专家模糊PID控制器进行控制.其中模糊PID控制器对系统分别对温度和流量进行直接控制，专家控制对模糊控制器的相关参数进行实时优化.

1.2 集中供热管网中流量控制系统模型的建立

该集中供热管网流量控制系统针对一次网电动调节阀和二次网循环泵变频器频率分别建立专家模糊PID控制算法.构建了基于专家模糊PID的热网流量质量并调耦合模型控制系统，如图3所示.

该解耦控制系统是由专家模糊PID控制器和质量并调的被控对象组成，被控对象为供热管网的一次网供水电动电磁阀的开度和二次网循环泵变频器的频率.图3中质调通道是以一次网供水电动电磁阀开度为控制量，以二次网的供水温度为被控量；量调通道以二次网循环泵变频器频率为控制量，以二级网实时流量为被控量.控制系统分别利用温度计和电磁流量计实时采集温度信息和流量信息，将采集的数字信息进行存储，并采用专家模糊PID控制器模块分别对温度和流量进行实时的智能控制，从而计算出一次网供水电动电磁阀的开度大小和二次网循环泵变频器的输出频率值.

图3 集中供热系统的专家模糊PID控制器Fig.3 Expert fuzzy PID controller in the central heating system

图3中质调节和量调节主通道的解耦控制模型分别为W11和W22；解耦控制的耦合通道1的模型为W12，以二次网循环泵变频器的输出频率为控制量，二次网供水温度为被控量；解耦控制的耦合通道2的模型为W21，以一次网电动电磁阀的开度为控制量，二次网内流量为被控量.

2 专家模糊PID控制器的构建

本文专家模糊PID控制器中专家控制作为协调级，根据数据库和知识库，经推理来实现对模糊PID控制器的调整.其控制结构框图如图4所示.

图4 专家模糊PID控制器控制结构框图Fig.4 Structure block diagram of expert fuzzy PID controller

2.1 模糊PID控制器的设计

模糊PID控制主要包含模糊化处理、模糊推理及解模糊3部分[9].模糊化是将系统的输入参量转换为模糊量，即将误差e和误差变化率ec转换为模糊量作为模糊控制器的输入量；对基本论域进行处理，将其转化成为对应的模糊论域；模糊推理是通过专家经验和知识，构建模糊控制的规则表，并结合模糊论域对PID控制器的Δkp、Δki、Δkd进行整定；解模糊采用重心法（Centroid Method），最终得到kp（k）、ki（k）、kd（k）的实时值，并按增量PID计算公式得出被控对象的控制参量Δu（k）.

模糊化处理分为2个部分：温度的模糊化处理和流量的模糊化处理.将温度和流量的误差及它们的误差变化率作为系统输入参量，输入模糊PID控制器，由基本论域转化成模糊论域.温度误差e的基本论域为 [-15，15]，温度误差变化率ec取 [-1.5，1.5]；流量误差e的基本论域为 [-6，6]，流量误差变化率ec取 [-0.6，0.6].输入变量e和ec的模糊子集为 {正大、正中、正小、零、负小、负中、负大}，记为 {PB，PM，PS，ZO，NS，NM，NB}，再将其量化到模糊论域 [-3，3]内.两条边界隶属函数NB和PB选用高斯型隶属函数，考虑到计算方便和控制精度等因素，其余选用三角形隶属函数.温度的量化因子为，流量的量化因子为

通过试凑法得出模糊PID控制器的初值，然后对系统进行实时整定得出相关参数的值.采用重心法将模糊推理得出的数据进行解模糊.参照温度控制及流量控制相关参数的模糊控制规则表，即可得到PID控制器Δkp、Δki、Δkd的实时数据，由公式（5）计算出k时刻实时PID参数值，并带入到公式（6）中得出k时刻被控对象的控制量Δu（k）.

2.2 专家系统规则的设计

在模糊PID控制器中，量化因子Ke和Kec如采用固定值将会对系统的稳态精度和动态响应产生影响.采用专家控制对模糊PID控制器的量化因子Ke和Kec进行调整，通过建立专家数据库和知识库，在记录控制器的相关参数的同时对量化因子Ke和Kec进行实时动态的调整，保证控制系统的灵活性和稳定性.

量化因子Ke和Kec对系统的影响可通过固定其中1个值，改变另一个值得出单个量化因子对系统的影响.通过实验可以得出误差的量化因子Ke对系统的影响主要有3点：

1）Ke值越大，系统的惯性越小，导致响应曲线上升速率越快；

2）Ke值超过一定范围，系统的响应曲线上升过快，会产生超调增大，调节时间增长，甚至产生严重振荡；

3）Ke值低于一定范围，系统的响应曲线上升过慢，惯性增大，收敛速度降低.

误差变化率的量化因子Kec对系统的影响主要有3点：

1）Kec值越大，系统的收敛速度降低，稳定性提高；

2）Kec值超过于一定范围，系统输出上升速率过慢，导致过渡时间增长；

3）Kec值低于一定范围，导致系统输出上升速率增大，出现超调和振荡现象，影响系统的稳定性.

图5中采用分段的方法将常规闭环系统阶跃响应曲线进行划分，并对各段曲线进行相应分析[10].

a1→b1段：该段为控制系统由静态到动态再向稳态转变的关键阶段，由于惯性只能呈倾斜方向上升.当该段采用固定参数控时，其制效果不佳，因此对其进行变参控制.在跟踪输出初始阶段，因输出最大控制量，同时Ke取最大值，Kec取最小值，这样才能保证系统输出上升时间大量缩短.给系统输出设定阈值emax（实验表明，取稳态值的10%～30%比较理想），当系统输出接近阈值时，应增大Kec，同时减小Ke，减小系统输出的惯性.在缩短调节时间的同时也减小了超调量的值.

b1→c1，d1→a2段：系统已出现超调.此时因及时调整参数，减小超调量，使输出值与设定值吻合，因此增大Kec并减小Ke来实现控制效果.

c1→d1，a2→b2段：系统输出曲线与设定值相吻合.该阶段系统已调整到平衡状态，故保持Ke和Kec值不变.

图5 常规闭环系统的阶跃响应曲线Fig.5 Step response curve of the conventional closed loop system

根据Ke和Kec对系统的影响分析及常规闭环系统阶跃响应曲线特性，得出专家控制规则：

1）IF e＞0 and ec＜0 and e＞emax，THEN Ke（k）=Kemax，Kec（k）=Kecmin；

2）IF e＞0 and ec＜0 and e≤emax，THEN Ke（k）=Ke1-ΔKe，kec（k）=Kec1-ΔKec；

3）IFe×ec＞0，THEN Ke（k）=Ke1-ΔKe，Kec（k）=Kec1-ΔKec；

4）ELSEKe（k）=Ke1，Kec（k）=Kec1.

Kemax为误差量化因子Ke阈值最大值；Kecmin为误差变化率量化因子Kec阈值最小值；emax为系统输出阈值；Ke1和Kec1为Ke和Kec的前一采样周期的数值.ΔKe和ΔKec分别为其增量，其值可依据实际情况适当选取.

3 系统的仿真实验研究

为了验证本文采用的改进专家模糊PID控制器在城市集中供热质量并调耦合系统的运行效果，选取MATLAB软件作为平台，将改进专家模糊PID控制器控制结果与常规的模糊PID控制器控制结果进行分析对比.设定二次网的起始供水温度为50℃，二次网水循环流量为156 m3/h.在专家模糊PID控制器中，供水温度控制的初始控制参量：KP0=0.1，KI0=0.11，KD0=0.01，初始量化因子为，Kec=2；二次网水循环流量控制的初始控制参量为KP0=0.3，KI0=0.7，KD0=0，初始量化因子为，Kec=5.

仿真时同时改变二次网供水温度Rin1和二次网流量Rin2的给定值，即Rin=（Rin1，Rin2） =（50，156），给定值分别通过改进前后的专家模糊PID解耦控制器结合集中供热耦合模型，得到二次网供水温度和二次网循环水流量的实时输出Yout=（Yout1，Yout2）.

实验中每隔0.2×104s给设定输入1个阶跃信号，设定值为Rin=（52，148）、Rin=（50，144）、Rin=（48，152）和Rin=（50，156），仿真结果如图6和图7所示.

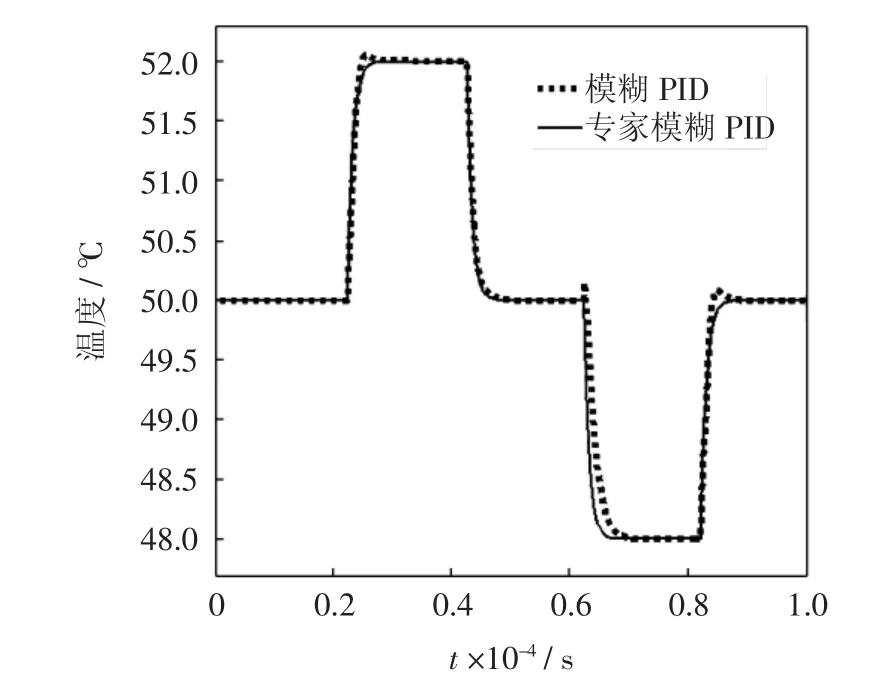
图6 质调节控制结果Fig.6 Result of qualitative regulation control

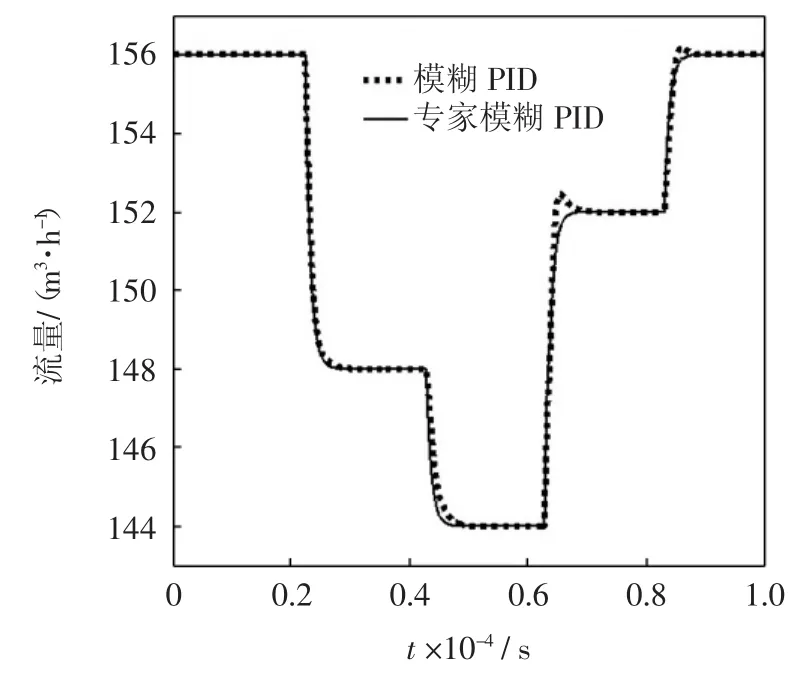
图7 量调节控制结果Fig.7 Result of quantitative regulation control

专家模糊PID控制器和模糊PID控制器的实验结果对比如表1所示.

表1 模糊PID和专家模糊PID解耦控制器的实验结果对比Tab.1 Comparison of experimental results between fuzzy PID controller and expert fuzzy PID controller

从图6、图7以及表1所示的实验结果对比，可以得出以下结论：

1）专家模糊PID控制器可更好地完成供热管网的解耦控制；

2）与模糊PID控制相比，专家模糊PID控制器在调节时间和超调量等控制指标方面均有改善，提高了解耦控制的精度和稳定性.该控制方法目前运用于天津市滨海新区的多个小区，均取得了良好的控制器效果.

4 结论

本文设计了改进的专家模糊PID控制器，用以解决城市集中供热系统流量的质量并调的耦合问题.采用专家系统实时地对模糊PID控制中的量化因子Ke和Kec进行调整，有效地提高了温度控制和变频控制的静态稳定速度和动态自适应能力.该方法为城市集中供热的管网流量优化控制提供了新思路，具有广阔的应用前景.

[1]张弘.专家-模糊自适应PID控制系统的设计[J].西安邮电学院学报，2009，14（1）：105-107.

[2]StefanovskiJ.Sufficien conditions for linear control system decouplingby static state feedback[J].Institute of Electrical and Electronics Engineers Inc. IEEE Transactions on Automatic Control，2001，46（6）：984-990．

[3] 闵娟，黄之初.多变量解耦控制方法[J].控制工程，2005，12（7）：125-127.

[4]Chen B，Tong S，Liu X.Fuzzy approximate disturbance decoupling of MIMO nonlinear systems by backstepping approach[J].Fuzzy Sets and Systems，2007，158（10）：1097-1125.

[5]朱林，吴冬雪，柴玲.神经元网络控制器在热网中的应用研究[J].自动化仪表，2014，35（12）：71-74.

[6]Chen M，Chen W H，Wu Q X.Adaptive fuzzy tracking control for a class of uncertain MIMO nonlinear systems using disturbance observer[J].Science China Information Sciences，2014，57（1）：1-13.

[7] 李红光，张国钧.换热站自动控制系统设计[J].自动化仪表，2015，36（3）：36-39.

[8]陈烈.基于神经网络的热力站供热过程预测控制研究[D].哈尔滨：哈尔滨工业大学，2009.

[9]洪炎，苏静明，唐超礼，等.基于专家-模糊PID的冻结凿井智能流量控制研究[J].计算机工程与科学，2012，34（7）：166-171.

[10]周彦，何小阳，王冬丽.时变大滞后过程的专家模糊控制设计与仿真[J].系统仿真学报，2006，18（10）：2786-2789.

[责任编辑 田 丰 夏红梅]

Research on optimal heat flow distribution in urban central heating system

YANG Weidong，XU Xiaowei，JIA Pengfei，MA Yuanyuan，HE Xiaodong
（School of Mechanical Engineering,Hebei University of Technology,Tianjin 300130,China）

The coupling relationship between qualitative regulation and quantitative regulation in the central heating system has been a key problem to its control performance.There also exist hysteresis,time variability and parameter uncertainty and other factors affecting the central heating system.To solve the above problems,an improved expert fuzzy PID control method is proposed to decouple the collaborative control mode.To further improve the accuracy of the fuzzy PID controller,the expert system is used to optimize the quantization of factor.Finally,the improved expert fuzzy PID controller is simulated and verified.As the simulation results show,compared with the conventional fuzzy PID controller,the improved expert fuzzy PID controller can not only realize the decoupling control between qualitative regulation and quantitative regulation of the central heating system,but also have better dynamic characteristics.

central heating;decoupling control;expert control;fuzzy PID control

TP202.7

A

1007-2373（2017）01-0053-08

10.14081/j.cnki.hgdxb.2017.01.009

2016-11-25

河北省自然科学基金（E2016202297）

杨伟东（1972-），男，教授，博士.