基于广义线性模型的师范生教师职业教学技能应用研究*

周 杰，洪河条，李国强，王国湖

（1.杭州师范大学 现代教育技术中心，浙江 杭州 311121；2.杭州师范大学 教育学院，浙江 杭州311121）

基于广义线性模型的师范生教师职业教学技能应用研究*

周 杰1，洪河条2，李国强2，王国湖2

（1.杭州师范大学 现代教育技术中心，浙江 杭州 311121；2.杭州师范大学 教育学院，浙江 杭州311121）

文章以浙江省师范生教学技能大赛参赛选手作为研究对象，从师范生成长过程角度考察师范生的教师职业教学技能发展的路径和影响因素。以浙江省师范生的教师职业教学技能竞赛数据为实证依据进行广义线性模型的建模，探讨了影响师范生的教师职业教学技能因素之间的关系。研究表明：性别因素对师范生的教学技能水平无显著影响；以师范教育为主的高等院校相较于其他院校表现较好；各个学科专业的师范生信息化素养水平较好。

广义线性模型；Logit回归模型；师范生；教学技能

一、问题的提出

师范生的教师职业教学技能[1]包括口语表达技能、书面表达技能、教学工作技能（教学设计的技能、使用教学媒体和编制教学软件的技能、课堂教学技能、设计和批改作业的技能、组织和指导学科课外活动的技能、教学研究的技能）、班主任工作技能（集体教育的技能、个体教育的技能、与任课教师和学生家长的沟通技能）等方面，主要是教师开展教育教学活动必备的技能。教师作为一种专门的职业，需要师范生（未来从业者）经过一套严格的、科学的专业知识和专门技术的训练才能胜任[2]。教学技能是教师在长期的教学实践中形成的一种熟练而灵活多变的能力，同时也是培养合格的师范生训练的重点内容。目前，政府、专家以及学者在师范生的教学技能培训和考核中做了积极而有益的探索。有学者提出信息技术与教育教学深度融合深刻影响着教师的教学技能结构，伴随着课堂教学模式的变化，必然对师范生教学技能的培养提出新的要求，信息技术能力也将纳入师范生必须具备的教师职业教学技能范围。再比如，由浙江省教育厅、浙江省教育技术中心、各市县教育局等政府部门协同各级各类高等学校开展浙江省师范生教学技能竞赛[3]，旨在主动适应并服务于基础教育改革发展对师资培养的需求，促进师范生教学能力的提升，同时也是衡量师范生的教师职业教学技能水平的有益尝试。

在“互联网+”时代背景下，为了适应新课程改革和新的教学模式，培养达到专业化标准的教师队伍，应改变过往对师范生的教师职业教学技能粗略地、描述性统计整体水平的研究，转向精确化、深层次量化的研究方法，进而深入剖析师范生的教师职业教学技能水平与各类因素之间的关系或者影响因素。因此，本文以浙江省师范生教学技能大赛参赛选手作为研究对象，从师范生成长过程角度考察师范生的教师职业教学技能发展的路径和影响因素。以浙江省师范生的教师职业教学技能竞赛数据为实证依据进行广义线性模型的建模，根据浙江省高等学校师范生教学技能大赛中的年龄、学校、专业、参赛科目等各个属性或类别因素逐步构建出Logit回归模型的饱和模型，能够更加客观、科学而全面地分析各个变量或者属性之间的内在联系，以期检验师资培养质量，加强教师基本技能的学习与训练，以促进教师教育的发展，提高师范生的教师教育教学基本素质和能力。

二、数据的选取与Logit回归模型的构建

1.数据来源及说明

浙江省高等学校师范生教学技能竞赛自2007年始每年开展一届，已经顺利完成九届大赛。该竞赛是一项封闭式大赛，由浙江省大学科技竞赛委员会主办。参赛选手选自浙江省高等学校师范专业全日制普通本科、专科在校大学生。竞赛由“教学设计、课件制作、模拟上课、即席演讲”四个部分组成，竞赛组别分为普通组、学前组、职教组，其中普通组包含语文、数学、外语、综合一、综合二、综合三，综合一组包含历史、思想政治、历史与社会、心理、地理，综合二组包含物理、化学、生物、科学、信息技术，综合三组包含音乐、体育、美术。竞赛评审由竞赛评审专家组负责，专家组成员由各有关高等学校推荐的师范教育专家以及若干名基础教育一线的特级教师组成，各校有参赛组别的每组推荐两名。本文选取浙江省高等学校师范生某一届教学技能大赛为研究数据，参赛选手来自浙江省内17所高等学校院校30个科目方向的282名师范生，其中普通组221名、职教组24名、学前组37名。竞赛数据多数为属性数据：参赛组别、参赛科目、参赛学校、参赛者姓名、参赛者性别、指导老师等。竞赛流程环节有150分钟完成教学设计并制作课件、3分钟即席演讲和10分钟模拟上课，共计四个项目。每个项目中有5位评委根据参赛选手表现打分，取5位评委的平均分作为该项目的分数，最后将参赛选手四个项目的得分按照权重计算得到选手参赛的最终分数，数据条目示例如表1所示。

在获取的源数据中，有部分数据缺失的情况，如参赛选手遇突发状况临时放弃比赛4人，针对这类数据我们直接删除。再加之，师范生专业的特点，竞赛人数有限，某些类别的参赛选手样本量较小，参数选手女生占据相当大的比重，中、低学段以及高学段的男生较少。综上，我们删除缺失的数据之后得到有效数据208条。

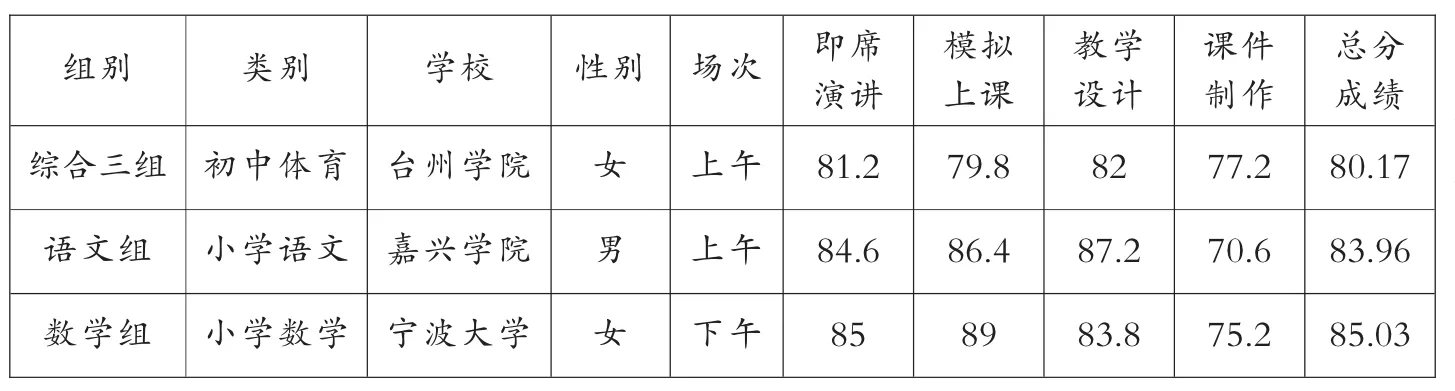
表1 数据条目

2.构建Logit回归模型

广义线性模型是线性模型的扩展，其特点是不强行改变数据的自然度量，数据可以具有非线性和非恒定方差结构。对数线性模型作为广义线性模型中一种重要、成熟的模型，是指导数据中因变量及因变量之间的相关关系非常重要的模型。Logit回归模型[4]是处理属性数据资料的统计模型，是处理具有非线性相关的离散变量的统计处理方法。以n个变量为例，当n个变量相互不独立时，建立的logit回归模型是饱和模型。饱和模型的形式如公式1所示：

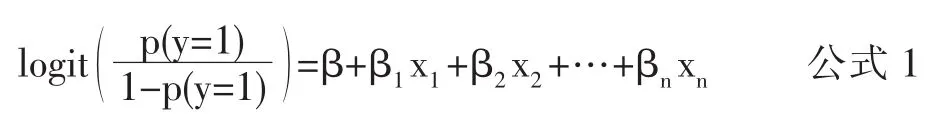
这里的p(y=1)是响应变量y成功的概率，y成功概率服从0-1二项分布；β为其他因变量一致时响应变量y成功的优势比 （也即截距项的优势比）；β1为因变量xi对应的因变量增加一个单位时优势比增加值。当因变量的优势比值大于0时，说明随着因变量的值增加，响应变量y成功的优势在增加；当因变量的优势比值小于0时，说明随着因变量的值增加，响应变量y成功的优势在减小；当因变量优势接近于0时，表明随着因变量的值增加，响应变量y成功的优势没有发生变化，由此进一步表明因变量对于响应变量的影响较小。

在实际的数据分析中，通常除了因变量的主效应项以外，各个因变量之间存在着交互作用，饱和模型的拟合效果不一定最好。因而，需要根据变量之间的独立性关系，选择合适的模型才能得到较好的模型拟合效果。好的模型既能充分拟合数据，又能最大程度的发现数据中的信息。首先，我们考虑饱和模型，形式如公式2所示：

在模型拟合结果发现，模型参数估计算法无法聚合，仔细研究发现，原始数据只有208个，但是饱和模型中参数已经不止208个了，因此必须考虑从饱和模型中逐步筛选变量。经过模型筛选过程发现，仅有包含主效应项的模型是能够拟合数据的。为此建立仅有主效应项的模型，如公式3所示：

根据“性别”、“学校”、“专业”、“类别”等变量之间的独立性关系，考察4个自变量两两之间以及与总分的相关关系。例如，检验性别与组别的相关关系，得到如下的列联表：对性别、组别做卡方检验时，卡方值为13.527，自由度为6，P-值为0.03539。

可见，性别与组别有着显著的相关关系，说明4个自变量之间存在着较强相关关系，但在自变量中，数据分布的不均衡性非常明显，使得只能建立仅包含住效应的logit模型。

类似的，性别、组别、学校、类别与总分之间都存在着相关关系，统计4组变量的卡方值和显著性结果时，汇总如表2所示。

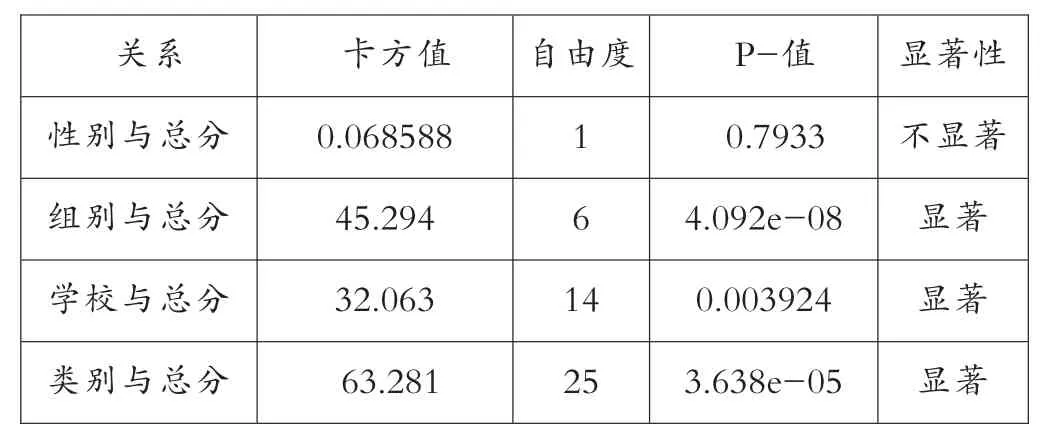
表2 四组变量的卡方值与显著性结果

另外，针对“组别”、“学校”、“类别”变量中某些变量显著性检验不通过的情况，考虑将“组别”、“学校”、“类别”中不显著的类别合并。例如，将组别中“综合一组”、“综合三组”、“外语组”合并为“其他组”，将类别中除“小学语文”、“小学数学”、“初中思品”、“初中数学”、“初中英语”之外的学科合并为“其他组”。

经过模型变量的筛选以及对于4个变量取值的重新设定，我们建立了如下的logit回归模型，如公式4所示：

三、实证结果分析

建立logit模型后，应对各个效应的估计值是否显著进行检验。通过对效应系数的显著性可以判断该效应在模型中是否合理。对数线性模型系数的检验通常用Z检验法。模型系数的检验结果及参数估计值见表3。

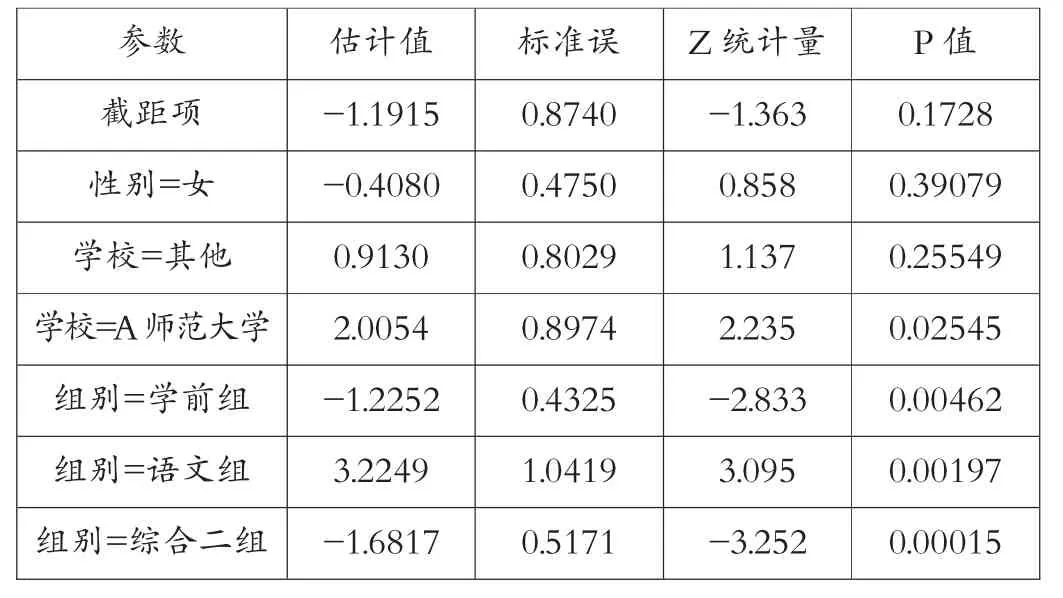
表3 模型系数检验结果及参数估计值

表3中，β=-1.1915，P值为0.1728>0.10，表明截距项不显著；β性别=-0.408，其中基线类别为女性，P值为0.3908，表明比赛结果中性别的差异不明显；β学校=其他= 0.9130，β学校=A师范大学=2.0054，基线类别为B大学，P值分别为0.25549和0.02545，表明相对于其他学校（包括B大学），A师范大学的学生比赛结果比较好；β组别=学前组=-1.2252，β组别=语文组=3.2249，β组别=综合二组=-1.6817，基线类别为其他组，3个组别的P值都小于0.10，表明3个组别相对于其他组别都是显著的；另外，由于所有类别的P值都是显著，综合了一些类别项仍然无济于事。在类别中，其实部分信息已经包含在组别之中了，例如外语组就包含了高中英语组、初中英语组、小学英语组，同时，由于类别中维度多达26项，模型中参入了学校、组别和性别等因素，使得模型有2*3*4*26=624项，但是样本数据中仅有208项，因此多数项拟合之后为0或者负值。因此，只能在模型中舍弃类别项。因此，最终的模型定位为如公式5所示：

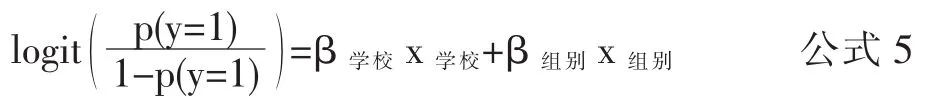
模型中，组别和学校是显著变量，在学校这个变量中，A师范大学、B大学（基线类别）的选手相对于其他学校的选手成绩比较优秀，同时，学前组、语文组以及综合二组的比赛选手相对其他组别的选手优势比较明显。

四、研究结论与不足

从实证结果我们得出以下结论：①在浙江省高等学校师范生教学技能竞赛中，性别因素对比赛成绩没有显著影响。也就是说，通过一系列教学技能训练之后，男生和女生在师范生的教师技能水平诸如口语表达技能、书面表达技能、教学工作技能以及信息化水平等方面表现差异不大。②以师范教育为主的高等师范类院校的表现成绩相较于其他院校在师范生教学技能的培养方面有一定的资源优势，主要是优秀的教师资源。③在专业类别上，由于国家政策对教育信息化的导向和财政支持，信息技术学科正逐步壮大，正逐步提升各个学科专业的师范生信息化素养水平。然而，不足之处在于样本数量小，参赛选手人数有限，这有待后续采用大数据样本开展分析，从而得到更全面和更准确的研究结果。

[1]高等师范学校学生的教师职业技能训练大纲[DB/OL].http://wenku.baidu.com.

[2]钟启泉.现代教学论发展[M].北京:教育科学出版社,1988:84.

[3]关于举行浙江省高等学校师范生教学技能竞赛. [DB/OL].http://www.zjcontest.net/zjcontest/index.

[4]Luce,R.D.(1959/2005)Individual Choice Behavior:A TheoreticalAnalysis.New York:Wiley. Reprinted by Dover Publications.

（编辑：鲁利瑞）

G451

:A

：1673-8454（2017）06-0075-03

本文系浙江省社会科学界联合会研究课题成果 “数据挖掘技术优化教师网络学习共同体的应用研究”（课题编号: 2017Z06）；2014年教育部卓越教师项目《师德·师能·师艺并重的卓越小学全科教师培养创新与实践》阶段性成果。