Modulation of neuronal dynamic range using two different adaptation mechanisms
2017-04-07
Neuroscience and Intelligent Media Institute, Communication University of China, Beijing, China
Modulation of neuronal dynamic range using two different adaptation mechanisms
Lei Wang*, Ye Wang, Wen-long Fu, Li-hong Cao
Neuroscience and Intelligent Media Institute, Communication University of China, Beijing, China
How to cite this article:Wang L, Wang Y, Fu WL, Cao LH (2017) Modulation of neuronal dynamic range using two different adaptation mechanisms. Neural Regen Res 12(3):447-451.
Open access statement:This is an open access article distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 License, which allows others to remix, tweak, and build upon the work non-commercially, as long as the author is credited and the new creations are licensed under the identical terms.
Funding:This research was supported by a grant from Beijing Municipal Commission of Science and Technology of China, No. Z151100000915070.
Graphical Abstract

The capability of neurons to discriminate between intensity of external stimulus is measured by its dynamic range. A larger dynamic range indicates a greater probability of neuronal survival. In this study, the potential roles of adaptation mechanisms (ion currents) in modulating neuronal dynamic range were numerically investigated. Based on the adaptive exponential integrate-and-fire model, which includes two different adaptation mechanisms,i.e. subthreshold and suprathreshold (spike-triggered) adaptation, our results reveal that the two adaptation mechanisms exhibit rather different roles in regulating neuronal dynamic range. Specifically, subthreshold adaptation acts as a negative factor that observably decreases the neuronal dynamic range, while suprathreshold adaptation has little influence on the neuronal dynamic range. Moreover, when stochastic noise was introduced into the adaptation mechanisms, the dynamic range was apparently enhanced, regardless of what state the neuron was in,e.g. adaptive or non-adaptive. Our model results suggested that the neuronal dynamic range can be differentially modulated by different adaptation mechanisms. Additionally, noise was a non-ignorable factor, which could effectively modulate the neuronal dynamic range.
nerve regeneration; dynamic range; subthreshold adaptation; suprathreshold adaptation; noise; neuron; adaptive exponential integrate-and-fire model; ion currents; computer simulation; neural regeneration
Introduction
In natural systems, the dynamic range serves as a good measure to characterize the capability of systems to discriminate between intensity of external stimulus. For example, in neuronal systems, this ability is important for biological cells to avoid danger. Tus, a larger dynamic range indicates a greater probability for neuronal survival (Gollo et al., 2012).
In past decades, several factors have been identified to modulate the dynamic range of neurons. Theoretical investigations suggest that a major effect of active dendritic conductance is to enhance the neuronal dynamic range, further revealing that neurons with larger dendritic trees may exhibit higher levels of dynamic range (Gollo et al., 2009). Trough the construction of computational network models of mammalian retina, researchers have shown that electrical synapses between rod-rod, along with appropriate values of rod Ih(hyperpolarization-activated cation current) conduc-tance, could enhance the dynamic range of retinal ganglion cells (Publio et al., 2009). Additionally, our recent model study demonstrated that intrinsic channel fluctuations exhibit a potent effect in modulating the neuronal dynamic range (Wang et al., 2013).
A prominent feature in biological neurons is their ability to adapt to processing afferent signals, called spike-frequency adaptation (SFA) (Chen et al., 2014; Wang et al., 2014c; Keller and Takahashi, 2015; King et al., 2015; Buonocore et al., 2016; Cui et al., 2016; Roach et al., 2016). Past studies focused on the ability of neurons to adapt to changes in incoming stimuli. In collision-detecting neurons, SFA has been shown to significantly contribute to neuronal tuning behaviors by selectively lowering the responses to non-preferred stimuli (Peron and Gabbiani, 2009). Experimental results on electroreceptor afferents showed that SFA helps separate transient signals from slower oscillatory signals in the background (Benda et al., 2005). Moreover, some studies suggested that SFA plays pivotal roles in defining neuronal population rhythms (Fuhrmann et al., 2002), spike timing precisions (Teka et al., 2014; Keller and Takahashi, 2015; Liu and Gollisch, 2015), and synchronous behaviors (Crook et al., 1998; van Vreeswijk and Hansel, 2001; Li et al., 2012; Pakdaman et al., 2014; Wang et al., 2014b; Norman et al., 2016).
Based on different generation mechanisms, adaptation can be classified into two types: subthreshold adaptation and suprathreshold (spike-triggered) adaptation. Previous reports demonstrated that these two adaptation mechanisms play differential functions in modulating neuronal spiking variability (Ladenbauer et al., 2014; Colliaux et al., 2015), regulating the correlation between sequential interspike intervals (Chacron et al., 2003; Shiau et al., 2015), and population synchronizations (Hansen and Dragoi, 2011; Ladenbauer et al., 2012).
In this study, we investigated how different SFA mechanisms (subthreshold and spike-triggered) influence the dynamic range of neurons. We also analyzed the effect of adaptation currents with stochastic fluctuations.
Materials and Methods
Neuronal model with adaptation currents
The model we employed to investigate was the adaptive exponential integrate-and-fire (aEIF) model, which has been widely used in previous model studies (Schwalger et al., 2010; Ladenbauer et al., 2012) to analyze SFA features in neurons (Hertäg et al., 2014; Buchin et al., 2016; Kobayashi and Kitano, 2016). The model includes the following equations and a reset condition (Schwalger et al., 2010; Ladenbauer et al., 2012):


with ancillary after-spike resetting according to the following equation (4):

whereCis the membrane capacitance,Vis the membrane potential of neuron,wis the adaptation variable,ηis an additional noise embedded in the adaptation dynamics, andIis the synaptic input.σcharacterizes the noise intensity of the adaptation current, andξ(t) denotes the Gaussian white noise.aquantifies the conductance that mediates subthreshold adaptation, andbquantifies suprashreshold adaptation through the increment in Eq. (4).Vcutrepresents the “cutoff” or maximum value ofV, andVrrepresents the resting potential ofV. Detailed explanations and values for the model parameters have been previously described (Schwalger et al., 2010; Ladenbauer et al., 2012). Specifically, gLis the leak conductance,VLis the leak reversal potential,ΔTis the threshold slop factor,VTis the threshold potential,τwis the adaptation time constant, and Nais the number of stochastic adaptation channels.
To characterize the dynamic range of a neuron, we introduced a widely used measure adopted from (Publio et al., 2009):

where,I90andI10represent the stimulus intensity for which the firing frequency of neuron is 10 percent below the maximum and 10 percent above the minimum, respectively.
Simulation method
Simulations were performed using Matlab software (R2010a) (The MathWorks, Natick, MA, USA), and the first-order Euler algorithm was employed to calculate the membrane potential with a time integration of 0.25 ms.
Results
Firing behaviors of an aEIF neuron
Figure 1demonstrates firing behaviors of an aEIF neuron under different adaptation states. Whena= 0 andb= 0, the neuron fired continuously with nearly identical interspike intervals, and no adaptation phenomenon was observed (Figure 1A). However, ifb= 0 anda> 0, ora= 0 andb> 0, the neuron fires spikes with apparent adaptation phenomena, suggesting that the firing frequency decreased and the interspike intervals were larger (Figure 1B,C).
Figure 2presents diagrams showing the variation of firing frequencies under different values ofaandb. Results showed that the increase ofamaintained the slope (gain) of the F-I (frequency-stimulus) curve, but the rheobase changed from low to high (Figure 2A). Although the increase inbmaintained the rheobase, the slope of the F-Icurve changed from high to low (Figure 2B). The variations of the F-I curves, which were due to the adaptation variablesaandb, were consistent previous reports (Ladenbauer et al., 2012).

Figure 1 Membrane potential and adaptation current of a typical adaptive exponential integrate-and-fire neuron.
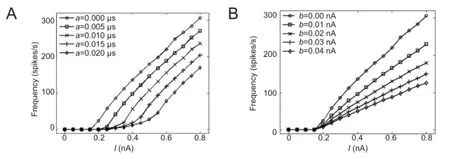
Figure 2 Frequency-stimulus (F-I) curves of adaptive exponential integrate-andfire neuron under different adaptation mechanisms.

Figure 3 Two-parameter dependence of neuronal dynamic range on the two adaptation mechanisms.

Figure 4 Membrane potential, adaptation current, and noisy current of an adaptive exponential integrate-and-fire neuron.

Figure 5 Variation of neuronal dynamic range with respect to noise intensity under different adapting states (repeating 50 times).
Dynamic range of neurons under different adaptation mechanisms
The variations of neuronal dynamic range with respect toaandbare demonstrated inFigure 3. Results show that sub-threshold adaptationaalways decreased the dynamic range of neurons, irrespective of the value ofb; while suprathreshold adaptationbhad little influence on the dynamic range when the value ofawas small. However, whenawas larger, the increase inbalso reduced the neuronal dynamic range.
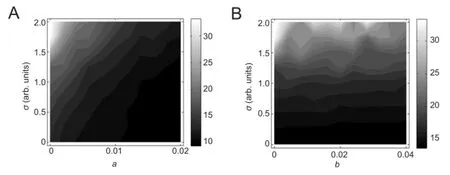
Figure 6 Two-parameter dependence of neuronal dynamic range on noise intensity and adaptation mechanisms (repeating 50 times).
Influence of noise on neuronal dynamic range
Noise is ubiquitous in natural systems, especially in neuronal systems (Andreeva, 2015; Béhuret et al., 2015; Mokri et al., 2015; Antal and Herrmann, 2016; Lee et al., 2016; Zylberberg et al., 2016). A previous study suggests that noise embedded in adaptation currents affects the shaping interspike interval histograms of spike trains and neuronal correlations (Schwalger et al., 2010). Terefore, we analyzed whether adaptation noise influenced the neuronal dynamic range.
Figure 4shows several examples of firing behavior of an aEIF neuron under different adaptation states. Compared with results fromFigure 1, the effect of noise on neuronal spikes was significant.Figure 5shows that the variations in neuronal dynamic range varied with increased noise intensity. The presence of noise always enhanced the neuronal dynamic range, regardless of the neuronal state (adaptive or non-adaptive).
The two-parameter dependence of neuronal dynamic range on noise intensity and variablesaandbis demonstrated inFigure 6. The reduction trend of neuronal dynamic range induced by an increasedawas always observed, regardless of the value of noise intensity. However, for fixed values ofa, the increased noise intensity reliably enhanced the dynamic range of neurons. Results fromFigure 6Bshowed that the variation trend of neuronal dynamic range induced by an increasedbalways persisted when the noise intensity varied. However, for fixed values ofb, the increased noise intensity also undoubtedly enhanced the neuronal dynamic range.
Discussion
SFA has been described as a prominent property in many neurons in the brain (Chen et al., 2014; Wang et al., 2014c; Keller and Takahashi, 2015; King et al., 2015; Buonocore et al., 2016; Cui et al., 2016; Roach et al., 2016). Previous studies revealed that SFA plays significant roles in neural information processing,e.g. modulating looming stimulus selectivity (Peron and Gabbiani, 2009), separating transient signals from background oscillations (Benda et al., 2005), mediating synchronous behaviors (Crook et al., 1998; van Vreeswijk and Hansel, 2001; Li et al., 2012; Pakdaman et al., 2014; Wang et al., 2014b; Norman et al., 2016), and reducing the variability of neuronal population activity (Schwalger et al., 2010). Results from the present study suggested that SFA exhibited crucial roles in regulating neuronal dynamic range. Moreover, the detailed regulations behave differently under the two adaptation mechanisms.
In the present paper, we performed a computational study to investigate whether adaptation mechanisms exerted influence on the dynamic range of biological neurons. Based on the aEIF model neuron, which includes two different adaptation mechanisms (subthreshold and suprathreshold), our results indicated that the two adaptation mechanisms had different roles in modulating the neuronal dynamic range: subthreshold adaptation decreased the dynamic range of neurons, while suprathreshold adaptation had little impact on the neuronal dynamic range. These results also suggested that noise embedded in the adaptation current efficiently adjusted the dynamic range of neurons, regardless of the neuronal state. Accordingly, these results could provide a better understanding about the factors that modulate the dynamic range of biological neurons.
Noise is a non-ignorable factor in natural systems, especially in neural systems (Andreeva, 2015; Béhuret et al., 2015; Mokri et al., 2015; Antal and Herrmann, 2016; Lee et al., 2016; Zylberberg et al., 2016). Previous studies have suggested a role for noise in processing neural information (Wang et al., 2014a; Nobukawa and Nishimura, 2015; Lücken et al., 2016). One recent study showed that noise embedded in adaptation currents performs critically in shaping the interspike interval histograms of spike trains and neuronal correlations (Schwalger et al., 2010). Results from the present study showed that adaptation currents with stochastic noise always enlarged the dynamic range of neurons.
It should be noted that we only discuss the effect of adaptation currents on modulating neuronal dynamic range in a single model neuron, but did not consider synaptic connections with many other neurons. In the nervous system, neurons are organized in networks or populations. Therefore, future studies should analyze the variations in dynamic range in neuronal networks.
Author contributions:All authors participated in the design, implementation, evaluation and data analysis of this study, and approved the final version of the paper.
Conflicts of interest:None declared.
Plagiarism check:This paper was screened twice using CrossCheck to verify originality before publication.
Peer review:This paper was double-blinded and stringently reviewed by international expert reviewers.
Andreeva E (2015) The relationship of tuning and noise correlations in macaque auditory cortex. J Neurosci 35:12974-12976.
Antal A, Herrmann CS (2016) Transcranial alternating current and random noise stimulation: possible mechanisms. Neural Plast 2016:3616807.
Béhuret S, Deleuze C, Bal T (2015) Corticothalamic synaptic noise as a mechanism for selective attention in thalamic neurons. Front Neural Circuits 9:80.
Benda J, Longtin A, Maler L (2005) Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci 25:2312-2321.
Buchin A, Rieubland S, Häusser M, Gutkin BS, Roth A (2016) Inverse stochastic resonance in cerebellar Purkinje cells. PLoS Comp Biol 12:e1005000.
Buonocore A, Caputo L, Pirozzi E, Carfora MF (2016) A leaky integrate-and-fire model with adaptation for the generation of a spike train. Math Biosci Eng 13:483-493.
Chacron MJ, Pakdaman K, Longtin A (2003) Interspike interval correlations, memory, adaptation, and refractoriness in a leaky integrate-and-fire model with threshold fatigue. Neural Comput 15:253-278.
Chen S, Benninger F, Yaari Y (2014) Role of small conductance Ca²+-activated K+channels in controlling CA1 pyramidal cell excitability. J Neurosci 34:8219-8230.
Colliaux D, Yger P, Kaneko K (2015) Impact of sub and supra-threshold adaptation currents in networks of spiking neurons. J Comput Neurosci 39:255-270.
Crook SM, Ermentrout GB, Bower JM (1998) Spike frequency adaptation affects the synchronization properties of networks of cortical oscillations. Neural Comput 10:837-854.
Cui Y, Wang YV, Park SJH, Demb JB, Butts DA (2016) Divisive suppression explains high-precision firing and contrast adaptation in retinal ganglion cells. Elife 5:e19460.
Fuhrmann G, Markram H, Tsodyks M (2002) Spike frequency adaptation and neocortical rhythms. J Neurophysiol 88:761-770.
Gollo LL, Kinouchi O, Copelli M (2009) Active dendrites enhance neuronal dynamic range. PLoS Comp Biol 5:e1000402.
Gollo LL, Mirasso C, Eguíluz VM (2012) Signal integration enhances the dynamic range in neuronal systems. Phys Rev E Stat Nonlin SoftMatter Phys 85:040902.
从广州出发飞 行了16个小时,再坐上2小时的大巴,穿越一片片平坦开阔的葡萄园、橄榄园,路过一栋栋白色或浅黄色的石屋,终于抵达普利亚产区的中心城市:曼杜里亚。此时接近正午,阳光正好,清劲的海风扑面而来,一下子驱散了长途旅行的不适。空气中弥漫着橄榄香、泥土香,暖暖的,非常惬意。放眼望去,都是狭窄的石头街道、古老的石头房子和教堂,街上行人寥寥。
Hansen BJ, Dragoi V (2011) Adaptation-induced synchronization in laminar cortical circuits. Proc Natl Acad Sci U S A 108:10720-10725. Hertäg L, Durstewitz D, Brunel N (2014) Analytical approximations of the firing rate of an adaptive exponential integrate-and-fire neuron in the presence of synaptic noise. Front Comput Neurosci 8:116.
Keller CH, Takahashi TT (2015) Spike timing precision changes with spike rate adaptation in the owl’s auditory space map. J Neurophysiol 114:2204-2219.
King JL, Lowe MP, Crowder NA (2015) Contrast adaptation is spatial frequency specific in mouse primary visual cortex. Neuroscience 310:198-205.
Kobayashi R, Kitano K (2016) Impact of slow K(+) currents on spike generation can be described by an adaptive threshold model. J Comput Neurosci 40:347-362.
Lücken L, Popovych OV, Tass PA, Yanchuk S (2016) Noise-enhanced coupling between two oscillators with long-term plasticity. Phys Rev E 93:032210.
Ladenbauer J, Augustin M, Obermayer K (2014) How adaptation currents change threshold, gain, and variability of neuronal spiking. J Neurophysiol 111:939-953.
Ladenbauer J, Augustin M, Shiau L, Obermayer K (2012) Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Comp Biol 8:e1002478.
Lee J, Joshua M, Medina Javier F, Lisberger Stephen G (2016) Signal, noise, and variation in neural and sensory-motor latency. Neuron 90:165-176.
Li H, Liu WZ, Liang PJ (2012) Adaptation-dependent synchronous activity contributes to receptive field size change of bullfrog retinal ganglion cell. PLoS One 7:e34336.
Liu JK, Gollisch T (2015) Spike-triggered covariance analysis reveals phenomenological diversity of contrast adaptation in the retina. PLoS Comp Biol 11:e1004425.
Mokri Y, Worland K, Ford M, Rajan R (2015) Effect of background noise on neuronal coding of interaural level difference cues in rat inferior colliculus. Eur J Neurosci 42:1685-1704.
Nobukawa S, Nishimura H (2015) Enhancement of spike-timing-dependent plasticity in spiking neural systems with noise. Int J Neural Syst 26:1550040.
Norman SE, Butera RJ, Canavier CC (2016) Stochastic slowly adapting ionic currents may provide a decorrelation mechanism for neural oscillators by causing wander in the intrinsic period. J Neurophysiol 116:1189-1198.
Pakdaman K, Perthame B, Salort D (2014) Adaptation and fatigue model for neuron networks and large time asymptotics in a nonlinear fragmentation equation. J Math Neurosci 4:14.
Peron S, Gabbiani F (2009) Spike frequency adaptation mediates looming stimulus selectivity in a collision-detecting neuron. Nat Neurosci 12:318-326.
Publio R, Oliveira RF, Roque AC (2009) A computational study on the role of gap junctions and rod Ih conductance in the enhancement of the dynamic range of the retina. PLoS One 4:e6970.
Roach JP, Sander LM, Zochowski MR (2016) Memory recall and spike-frequency adaptation. Phys Rev E 93:052307.
Schwalger T, Fisch K, Benda J, Lindner B (2010) How noisy adaptation of neurons shapes interspike interval histograms and correlations. PLoS Comp Biol 6:e1001026.
Shiau L, Schwalger T, Lindner B (2015) Interspike interval correlation in a stochastic exponential integrate-and-fire model with subthreshold and spike-triggered adaptation. J Comput Neurosci 38:589-600.
Teka W, Marinov TM, Santamaria F (2014) Neuronal spike timing adaptation described with a fractional leaky integrate-and-fire model. PLoS Comp Biol 10:e1003526.
van Vreeswijk C, Hansel D (2001) Patterns of synchrony in neural networks with spike adaptation. Neural Comput 13:959-992.
Wang L, Zhang PM, Liang PJ, Qiu YH (2013) Enhancement of the neuronal dynamic range by proper intensities of channel noise. Chin Phys Lett 30:070506-070509.
Wang L, Liang PJ, Zhang PM, Qiu YH (2014a) Ionic mechanisms underlying tonic and phasic firing behaviors in retinal ganglion cells: a model study. Channels (Austin) 8:298-307.
Wang L, Zhang PM, Liang PJ, Qiu YH (2014b) Effects of spike frequency adaptation on synchronization transitions in electrically coupled neuronal networks with scale-free connectivity. Chin Phys Lett 31:070501.
Wang L, Liang PJ, Zhang PM, Qiu YH (2014c) Adaptation-dependent synchronization transitions and burst generations in electrically coupled neural networks. Int J Neural Syst 24:1450033.
Zylberberg J, Cafaro J, Turner Maxwell H, Shea-Brown E, Rieke F (2016) Direction-selective circuits shape noise to ensure a precise population code. Neuron 89:369-383.
Copyedited by Cooper C, de Souza M, Yu J, Li CH, Qiu Y, Song LP, Zhao M
*Correspondence to: Lei Wang, Ph.D., wanglei_nc@163.com.
orcid: 0000-0003-3460-1069 (Lei Wang)
10.4103/1673-5374.202931
Accepted: 2017-01-09
猜你喜欢
杂志排行
中国神经再生研究(英文版)的其它文章
- Anesthetic considerations for patients with acute cervical spinal cord injury
- Transplantation of autologous peripheral blood mononuclear cells in the subarachnoid space for amyotrophic lateral sclerosis: a safety analysis of 14 patients
- Anatomical distributional defects in mutant genes associated with dominant intermediate Charcot-Marie-Tooth disease type C in an adenovirusmediated mouse model
- Mechanisms responsible for the inhibitory effects of epothilone B on scar formation after spinal cord injury
- The mechanism of Naringin-enhanced remyelination after spinal cord injury
- Estrogen affects neuropathic pain through upregulating N-methyl-D-aspartate acid receptor 1 expression in the dorsal root ganglion of rats
