波形钢腹板连续箱梁的结构参数对其自振影响分析

李 杰， 周亚鹏， 陈 淮

(郑州大学 土木工程学院 河南 郑州 450001)

波形钢腹板连续箱梁的结构参数对其自振影响分析

李 杰， 周亚鹏， 陈 淮

(郑州大学 土木工程学院 河南 郑州 450001)

为了分析波形钢腹板连续箱梁桥的结构参数对其自振的影响，以郑州市陇海路高架常庄水库桥为依托，利用ANSYS软件建立3跨精细有限元模型，分析预应力、波形钢腹板的波折角度、单板宽度、腹板厚度等结构参数，以及横隔板数量对连续体系波形钢腹板组合箱梁自振特性的影响.分析表明：预应力张拉产生“应力软化”效应引起结构总刚度降低，结构的频率降低;另一方面，体外束预应力使得混凝土处于复杂应力状态，通过弹性模量修正，自振频率会随着预应力束张拉力的增大而增大，可与试验结果吻合；振动频率随波折角度的增大表现为先增大后减小，然后会出现小幅度增长；振动频率随着水平板宽的增加表现为先增大后减小；竖向振动频率、纵向振动以及扭转频率均随着腹板厚度的增加而增大，横向振动频率随着腹板厚度的增加而减小；增加横隔板数量能明显提高箱梁的扭转振动频率，但扭转频率的增长速率随着横隔板数量的增加逐渐降低.

结构参数； 波形钢腹板组合箱梁； 连续梁； 自振频率

0 引言

波形钢腹板组合箱梁采用波形钢板置换混凝土箱梁中的混凝土腹板，使箱梁成为由钢筋混凝土顶底板和波形钢腹板组成的组合结构，其充分利用了混凝土抗压和波形钢腹板抗剪强度高、梁体自重轻、顶底板预应力效率高的优点，是一种经济合理、绿色高效的桥梁主梁结构形式[1-3].桥梁结构的自振特性是桥梁工作性能和抗震、抗风等动力性能分析的重要参数，与桥梁的自身性质息息相关，新颁布的《公路桥涵设计通用规范》(JTG D60-2015)中公路汽车荷载冲击系数的计算仍然是以桥梁基频为参数[4]，因此桥梁结构的自振特性就成为结构设计的重要基础数据.一些学者通过模型试验和数值方法研究分析了波形钢腹板组合箱梁的自振频率[5-8]，并讨论了结构参数对结构自振特性的影响[9-13]，但针对连续体系波形钢腹板组合桥梁的研究还不多.随着组合桥梁的快速发展，连续、斜拉等结构体系逐渐增多，有必要对非简支体系的波形钢腹板组合桥梁的自振特性进行研究.本文以郑州陇海路高架常庄水库桥为依托，选取三跨连续梁结构体系，采用有限元数值方法，分析预应力、波形钢腹板的波折角度、单板宽度、腹板厚度等几何参数，以及横隔板数量对连续体系波形钢腹板组合箱梁自振特性的影响.

图1 郑州市陇海路高架常庄水库桥

1 依托工程及有限元建模

1.1 依托工程

郑州常庄水库桥作为郑州市陇海路快速通道工程的重要组成部分，是国内首次采用顶推施工建造的波形钢腹板组合箱梁，如图1所示.该桥全长940 m，跨径布置形式为(9 m×50 m)+(9 m×50 m+40 m)，上部结构为等高度的波形钢腹板预应力混凝土组合连续箱梁，左右幅断面对称布置，两幅之间设20 mm分隔缝.单幅断面采用单箱单室斜腹板截面，截面

顶缘采用双向2.0%横坡，梁底水平布置.波形钢腹板采用BCSW1600型，板厚采用16 mm和20 mm两种，顶底板设有体内和体外预应力束，腹板倾斜角度75°，箱梁中心高度为3.5 m，箱梁顶板悬臂长度为3.2 m，内室宽度为6.35 m，顶板悬臂端部厚度为0.2 m，根部厚0.55 m；顶板厚度为0.3 m，底板厚度为0.25 m，支点横梁处加厚至0.55 m.在靠近支点处的波形钢腹板侧面设置内衬混凝土，内衬段混凝土长度为3.2 m，端部厚0.3 m，根部厚0.6 m.箱梁标准断面见图2.

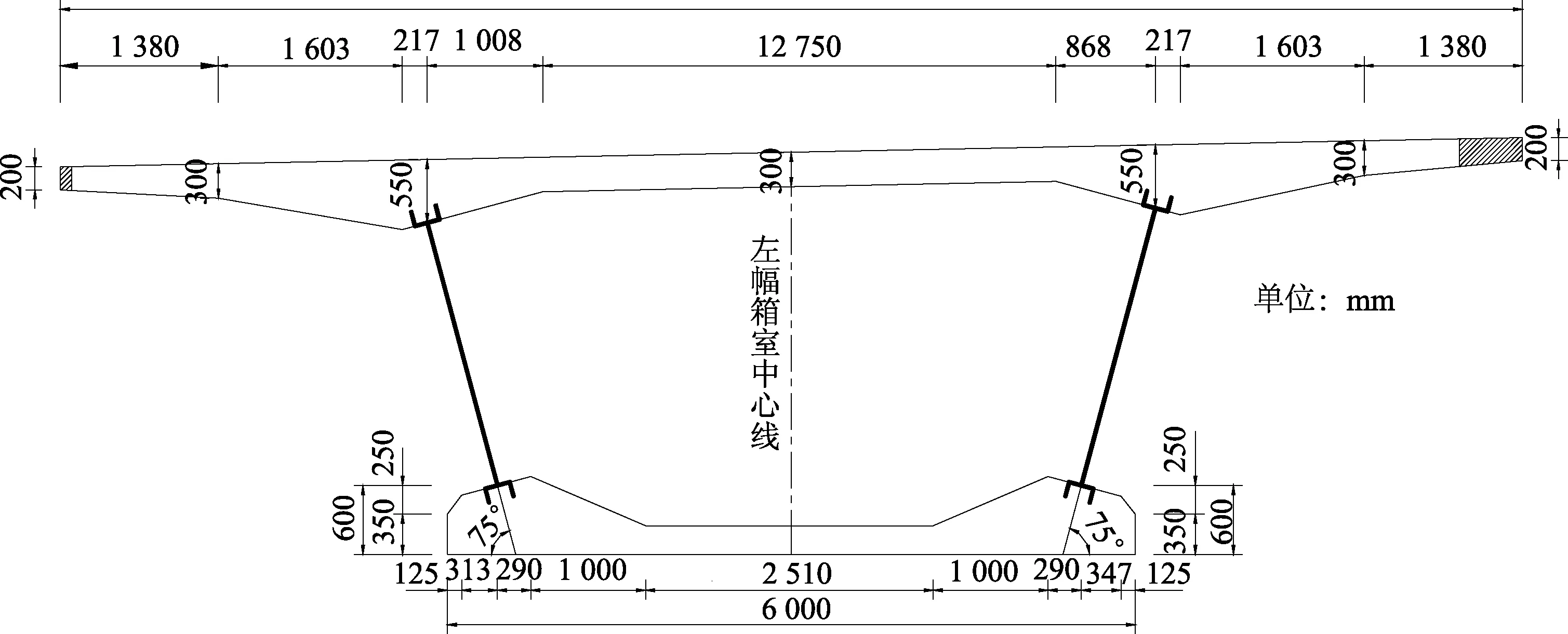
图2 波形钢腹板组合箱梁标准断面

1.2 有限元模型

考虑到常庄水库桥的结构形式相同，本文选取其中3跨连续体系进行研究，并采用ANSYS有限元分析软件建立常庄水库桥精细空间组合有限元模型.波形钢腹板箱梁顶、底板为混凝土板，且其横截面不规则，采用Solid65实体单元进行模拟，由于顶底板和波形钢腹板的连接处为折线，为使波形钢腹板和顶底板完全共节点，同时为方便映射网格划分，建模中注意保证在顶底板和波形钢腹板交界处建立完全吻合的波折线；端横隔梁、中横隔板位于箱梁的内部，均由混凝土浇筑而成，采用三维实体单元Solid65模拟；波形钢腹板的厚度16～22 mm，沿着箱梁轴向成波折形状布置，主要承担顶、底板传递来的剪力，沿轴向几乎没有抵抗作用，采用Shell63壳单元模拟，并通过定义实常数赋予波形钢腹板的厚度；按照施工图纸中体内、体外预应力束的位置，采用Link10单元模拟预应力筋.在有限元模型中，由于混凝土采用Solid65单元模拟，仅有3个平动自由度，而波形钢腹板采用Shell63壳单元模拟，每个节点有3个平动自由度以及3个转动自由度，当两者仅用共节点连接时软件中默认为铰接，弯矩无法在两者之间有效传递，而实际上波形钢腹板与顶、底板混凝土的连接部位可以限制波形钢腹板的转动，在弹性工作范围内，波形钢腹板和顶、底板混凝土能够完全共同受力，不会发生相对滑动或剪切破坏，两者之间的连接认为是刚性连接，因此在建立模型时通过两者共用节点并施加约束方程的方法进行准确模拟.此外，波形钢腹板是通过其内侧焊钉嵌入在内衬混凝土和横隔板中，从而使各构件共同受力协调变形，因此只要保证共节点就可以确保两者的有效连接.预应力束通过定义实常数赋予钢绞线面积，并采用初应变法模拟预应力张拉；在单元分别划分后，通过耦合命令将预应力束单元上的所有节点与离其最近的混凝土单元的节点耦合，从而使预应力钢束和混凝土连结成整体，并将预应力施加到混凝土上，进而实现两者的共同受力；对于体内预应力束，仅需预应力钢束节点和混凝土节点完全耦合，对于体外预应力钢束，每根预应力束的应力大小相同，可以采用相同的初始应变，中间节点在转向块处释放纵向自由度，径向与转向块节点耦合.

建立几何模型后，对全桥进行网格划分以建成有限元模型.混凝土实体采用高精度的六面体单元，波形钢腹板采用4节点的板壳单元.对混凝土单元和波形钢腹板单元进行划分时，全部采用映射网格划分.所建模型共61 352个实体单元，6 352个板壳单元，1 658个杆单元，97 446个节点.

2 波形钢腹板连续箱梁自振特性的影响因素分析

2.1 预应力的影响

根据预应力混凝土桥梁设计规范，针对YYL1～YYL6这6种工况(如表1所示)，分析预应力对波形钢腹板连续箱梁自振频率的影响.

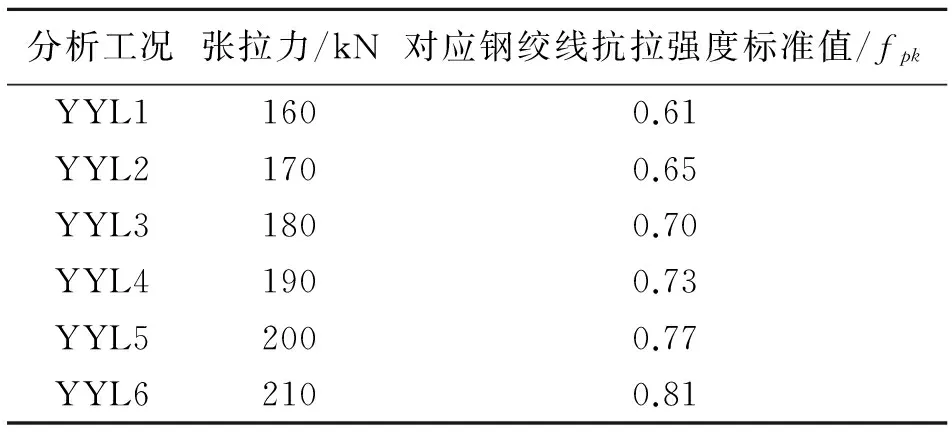
表1 预应力张拉分析工况

1阶竖向自振频率分析结果见表2.考虑到由于预应力的施加会产生“应力软化”效应，几何刚度矩阵引起结构总刚度降低，进而结构的频率降低，同时也可以看出预应力对波形钢腹板组合箱梁自振频率的影响较小.但该结论与一些模型试验结果不吻合[10]，不能解释试验中所反映出来的数据，预应力除了会产生“应力软化”效应降低结构的刚度外，还会使混凝土处于复杂应力状态.复杂应力状态下的混凝土极限强度比单向应力状态下的强度大，理论和试验证实混凝土的强度与弹性模量相关，那么可以通过建立预应力与混凝土弹性模量的相关关系，对复杂应力状态下的弹性模量进行修正[12],以便与实测数据吻合.文献[12]通过大量复杂应力状态下混凝土梁试验数据，采用回归分析的方法找出了预应力与混凝土弹性模量的关系，如公式(1)所示.

(1)

其中：y=Eq/Ec,表示混凝土弹性模量的增加倍数(Eq为等效的弹性模量，Ec为实际弹性模量);N表示施加的预应力大小;e表示偏心距;h表示箱梁截面高度;l表示跨径;A表示截面面积;fck表示混凝土抗压强度标准值;a、b、c分别表示拟合公式的系数，具体数值大小如式(2)所示.

a=-6.651 418 8×10-3;b=7.512 877 8×10-3;c=2.409 094 7×10-3.

(2)

表2为弹性模量修正与否的对比，可以看出对本文选定的波形钢腹板连续箱梁桥而言，当不修正混凝土的弹性模量时，波形钢腹板连续箱梁的各阶自振频率均会随预应力大小的增大而减小，这是由于施加预应力后几何刚度矩阵引起结构总刚度降低，进而结构的频率降低；当修正混凝土的弹性模量时，波形钢腹板连续箱梁的自振频率随预应力的增大而增大，这是由于除了“应力软化”导致的结构刚度降低外，还可能由于混凝土处于复杂应力状态，从而使混凝土弹性模量出现一定程度的增大，进而引起波形钢腹板连续梁桥的刚度增大，该结果也与试验数据较吻合[10].但总的来看，预压力张拉对波形钢腹板组合连续箱梁桥自振特性的影响不大.

表2 不同预应力下的1阶竖向自振频率

2.2 波形钢腹板结构形式的影响

波形钢腹板是波形钢腹板桥梁的重要组成部分，有必要研究其结构几何参数对自振频率的影响.目前国内外常用的波形钢腹板的波形主要有1600型、1200型和1000型3种，其中1600型是实际工程应用最多的一种波形，1200型与1000型主要应用于跨度较小的梁以及因运输困难需采用波长和波幅较小的桥梁.波形钢腹板的形状参数主要由水平板宽b、斜板的投影d、斜板水平投影长度c、板厚t和波形高度h组成，且d=bcosα，h=bsinα，其中：α表示波折角度.由此可得波形钢腹板的独立形状参数只有单板宽度b、波折角度α和板厚h.根据这3个参数，分别进行波形钢腹板的结构形式对波形钢腹板连续箱梁自振特性的影响分析.

2.2.1 波折角度α的影响 常庄水库桥采用的波形钢腹板波折角度为30.7°，参考国内外已建成的此类桥梁的波形腹板常用的波折角度[13]，选定斜板倾角分别采用25.1°、30.7°(1600型)、36.5°(1200型)、40.2°、45°(1000型)和50.7°，同时保证腹板厚度t=16 mm及单块钢板宽度b=430 mm不变.按照上述6种倾角依次建立BZJ1～BZJ6,分析工况的数值模型，限于篇幅取1阶竖弯、1阶横弯、纵向振动以及1阶扭转这4种振型的频率进行分析，见表3所示.

表3 不同波折角度下的自振频率

由表3可以得出：在25.1°～30.7°范围内，随着波折角度的增大，波形钢腹板的竖向振动、横向振动、纵向振动以及扭转振动的频率均会有所上升，提高幅度分别为2.11%、0.42%、0.37%和0.07%，表明随着波折角度的增大，提高了波形钢腹板连续箱梁的刚度，尤其是竖向刚度；在30.7°～36.5°范围内，随着波折角度的增大，波形钢腹板的竖向振动、横向振动、纵向振动以及扭转振动的频率均有所下降，下降幅度为2.88%、0.58%、0.80%和0.80%，表明在该角度范围内,随着波折角度的增大，反而减小了波形钢腹板连续箱梁的刚度，尤其是竖向刚度；在36.5°～50.7°范围内，随着波折角度的增大，波形钢腹板的竖向振动、横向振动、纵向振动基本表现为频率均会再次有所上升，但不能达到波折角度30.7°时产生的效果，扭转振动的频率表现为不断下降.综上所述，当波折角度取30.7°时，波形钢腹板箱梁的竖向刚度和扭转刚度达到最大，能一定程度提高波形钢腹板箱梁的抗弯和抗扭能力.工程上最广泛应用的1600型波形钢腹板就是采用此角度.

2.2.2 单板宽度b的影响 常庄水库桥的波形钢板采用单板宽度为430 mm.参考国内外已建成的此类桥梁的波形腹板采用的单板宽度[12]，单板宽度分别采用300 mm、330 mm(1200型)、360 mm、400 mm、430 mm(1600型)和512 mm，同时保证腹板厚度t=16 mm及波折角度α=30.7°不变，依次建立上述6个比较模型，限于篇幅取1阶竖弯、1阶横弯、纵向振动以及1阶扭转这4种振型的频率进行分析，见图3.

由图3可以看出，随着水平板宽b的增加，波形钢腹板混凝土箱梁的竖向振动、横向振动、纵向振动以及扭转振动频率总体都表现为先增大后减小.这主要是由于保持腹板厚度t和波折角度α不变，随着单板宽度的增大，波形钢腹板的波折高度也开始增大，从而使得波形钢板面外刚度也增大，所以会出现波形钢腹板箱梁的各向频率随着单板宽度的增大而增大的情况；然而当板宽过大时，波形钢板的整体受力性能减弱，反而会使梁的各向刚度降低.因此可以得出结论：在腹板厚度t和波折角度α一定的情况下，单宽度b有其最优的选取范围，大致为400～450 mm，工程中常用的1600型波形钢腹板采用的单板宽度为430 mm.

2.2.3 腹板厚度t的影响 常庄水库桥采用的波形钢腹板厚度为16～22 mm.工程中的波形钢腹板的最小板厚为8 mm，最大板厚为28 mm.参考已建成桥梁波形钢腹板采用的板厚参数值，取t=8 mm、12 mm、14 mm、16 mm、22 mm、28 mm这6种工程上常用的波形钢腹板厚度进行研究，同时保持水平板宽b=430 mm 及波折角度α=30.7°不变，研究上述6种工况.取1阶竖向弯曲、1阶横向弯曲、纵向振动以及1阶全桥扭转这4种振型的频率进行分析，详见图4.

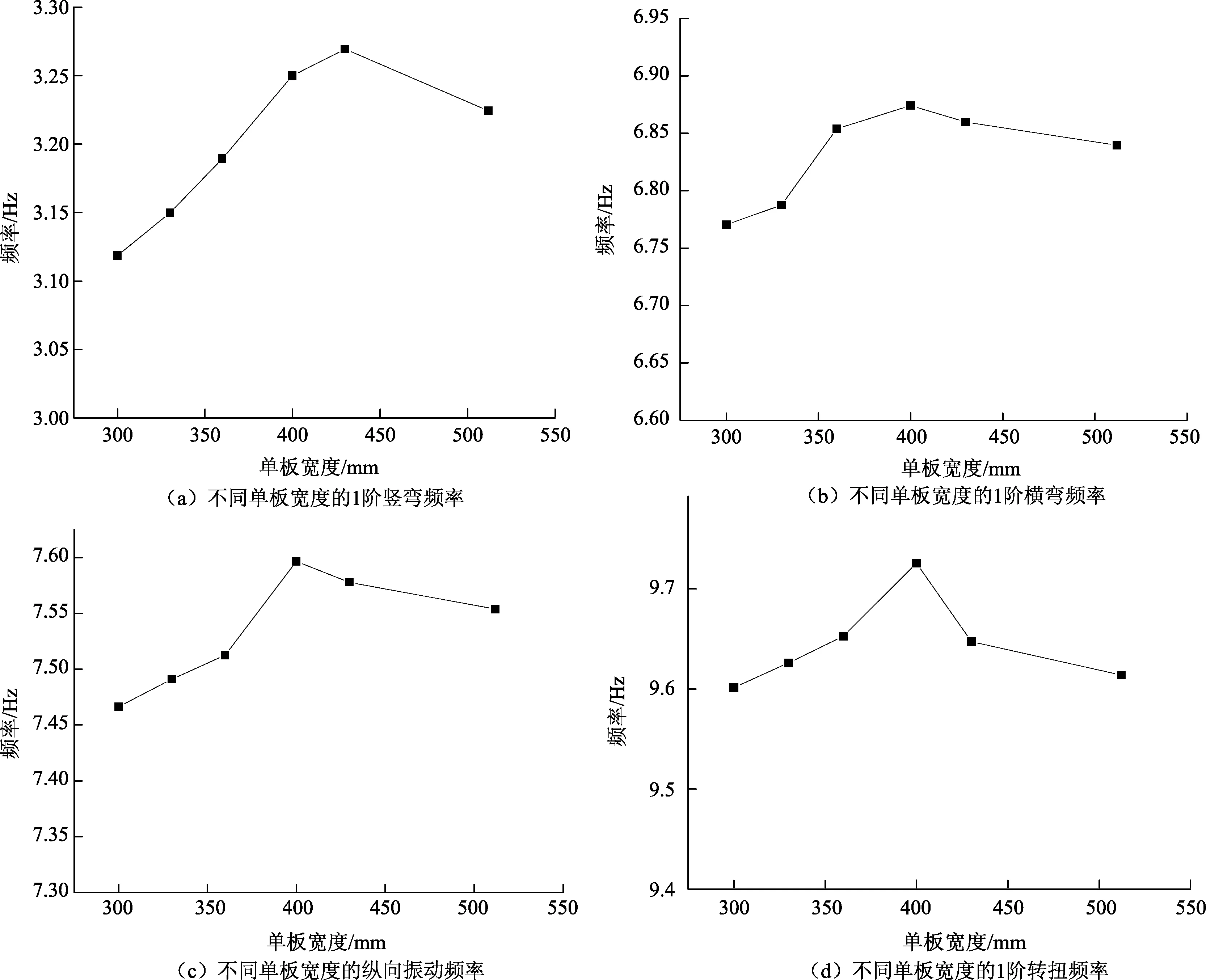
图3 单板宽度对自振频率影响

图4 腹板厚度对自振频率影响

由图4可以看出，波形钢腹板连续箱梁的竖向振动频率、纵向振动以及扭转频率均随着腹板厚度的增加而逐渐增大，最大增长幅度分别为7.10%、4.04%和27.27%，扭转频率增幅最大，这主要由于在单板宽度和波折角度一定的情况下，波形钢腹板厚度的提高能一定程度上提高箱梁的刚度.但是当其增大到一定值时箱梁的竖向、纵向刚度和扭转刚度的影响会逐渐减小；腹板厚度的增大会减小波形钢腹板连续箱梁的横向振动频率，最大减小幅度4.04%，这主要由于增加板厚会增大波形钢腹板箱梁的质量和横向刚度，但质量的增加更显著，横向刚度增加较小，综合考虑这两因素的变化，横向频率表现为下降.

2.3 横隔板的影响

采用波形钢腹板替代混凝土腹板，会使得波形钢腹板箱梁的抗扭刚度减小，为提高此类桥梁的抗扭能力,应设置必要的横隔板.在已建成的波形钢腹板桥梁中，中横隔间距多为8～25 m.以依托桥梁为参考，依次等间距设置0～5道横隔板，分析HGB1～HGB6这6种工况下的自振特性.限于篇幅取1阶竖弯、1阶横弯、纵向振动以及1阶扭转这4种振型的频率进行分析，详见表4.

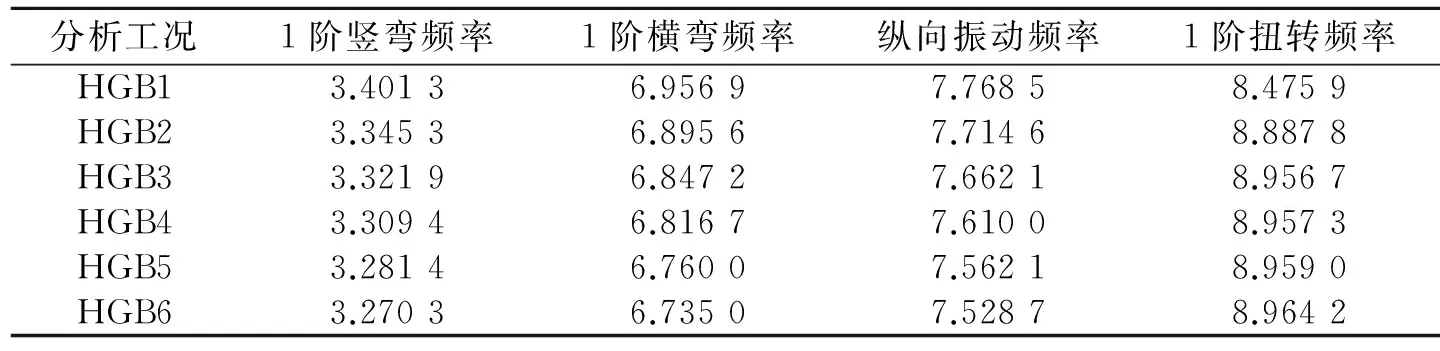
表4 不同横隔板数量下的自振频率

由表4可以看出：当横隔板数量增加时，波形钢腹板连续箱梁的竖向频率、横向频率以及纵向频率均表现为降低，最大降低幅度分别为4.00%、3.29%和3.19%.主要是由于波形钢腹板连续箱梁的竖向、横向、纵向刚度主要由顶底板混凝土提供.上述6种工况中，箱梁顶底板混凝土的规格完全相同，因此横隔板数量增多后，箱梁的刚度增加有限而重量增加明显，从而导致自振频率的下降；增设横隔板能明显提高波形钢腹板连续箱梁的扭转频率，且横隔板数量的增加会增大波形钢腹板连续箱梁的扭转频率，最大增加幅度为5.76%；扭转频率的增长速率随着横隔板数量的增加逐渐降低，其原因是增设横隔板能明显提高波形钢腹板连续箱梁的扭转刚度，故而增长明显，但由于横隔板数量增多后，箱梁重量增加过大而刚度增加有限，从而导致自振频率增长速率的下降.

3 结论

1) 对本文选定的波形钢腹板连续箱梁桥而言，综合考虑“应力软化”引起的刚度变化以及混凝土复杂应力状态引起的弹性模量变化这两种影响因素，自振频率会随着体内、体外束张拉力的增大而增大，可解释模型试验的实测数据.

2) 保持波形钢腹板的单板宽度b和厚度t不变，波形钢腹板连续箱梁的各向振动频率随波折角度α的增大均表现为先增大后减小，然后会出现小幅度增长，但整体看来，在波折角度α=30.7°附近达到最大，与目前工程实际应用的波折角基本一致.

3) 保持波形钢腹板的厚度t和波折角α不变，波形钢腹板混凝土箱梁的各向振动频率总体随着水平板宽b的增加都表现为先增大后减小；在腹板厚度t和波折角度α一定的情况下，水平面板宽度b有其最优的选取范围，工程中常用的1600型波形钢腹板采用的单板宽度为430 mm，与文中的结论相符.

4) 波形钢腹板连续箱梁的竖向振动频率、纵向振动以及扭转频率均随着腹板厚度的增加而逐渐增大，说明提高波形钢腹板厚度能一定程度上增大箱梁的抗弯刚度和抗扭刚度，但是当其增大到一定值时，箱梁的竖向、纵向刚度和扭转刚度的影响会逐渐减小；腹板厚度的增大对横向刚度影响小，反而使得波形钢腹板连续箱梁的横向振动频率减小.

5) 当横隔板数量增加时，波形钢腹板连续箱梁的竖向频率、横向频率以及纵向频率均表现为降低；增加横隔板数量能明显提高箱梁的扭转振动频率，且波形钢腹板连续箱梁的扭转振动频率随着横隔板数量的增加表现为增大，但扭转频率的增长速率随着横隔板数量的增加逐渐降低.

[1] 李杰，冯冠杰，陈淮．单箱四室波形钢腹板组合箱梁桥承剪分析[J]．桥梁建设，2016，46(2)：70-75．

[2] 陈海波．波纹钢腹板混凝土箱梁动力特性研究[D]．北京：北京交通大学，2007．

[3] 郑元勋，杨培冰.刚构桥梁悬臂施工挂篮设计及预加载试验研究[J].郑州大学学报(理学版)，2015，47(4)：108-112.

[4] 李杰，周明坤，陈淮．双薄壁高墩曲线多跨连续刚构桥自振特性分析[J]．郑州大学学报(理学版)，2015， 47(2)：109-114．

[5] 焦春节，丁洁民．体外预应力钢-混凝土组合连续梁自振频率分析[J]．工程力学，2011，28(2)：193-197．

[6] 张永健，黄平明，狄谨，等．波形钢腹板组合箱梁自振特性与试验研究[J]．交通运输工程学报，2008，8(5)：76-80．

[7] 冀伟，刘世忠，蔺鹏臻．波形钢腹板PC 连续箱梁桥自振频率分析与试验研究[J]．中南大学学报(自然科学版)，2016，47(4)：1297-1304．

[8] 石鲁宁，闫维明，何浩祥．多跨体外预应力连续梁动力特性研究-模态解析解[J]．振动与冲击，2014，33(16)：50-55．

[9] 冀伟，刘世忠，蔺鹏臻．波形钢腹板连续箱梁的动力特性[J]．公路交通科技，2011，28(11)：55-60．

[10] 郑尚敏，马磊，万水．体外预应力对波形钢腹板箱梁自振频率的影响分析[J]．东南大学学报(自然科学版)，2014，44(1)：140-144．

[11] 陈水生，陈志兴．横隔板对波形钢腹板箱梁动力特性的影响分析[J]．中外公路，2015，35(3)：77-79．

[12] 李瑞鸽，杨国立，张耀庭．预应力混凝土梁模态分析的有限元软件实现[J]．西安建筑科技大学学报(自然科学版)，2012，44(2)：188-192．

[13] 周亚鹏．波形钢腹板PC连续箱梁桥自振特性研究[D]．郑州：郑州大学，2016．

(责任编辑：王浩毅)

Influence of Structural Parameters on the Vibration of Continuous Box Girder with Corrugated Steel Webs

LI Jie， ZHOU Yapeng， CHEN Huai

(SchoolofCivilEngineering,ZhengzhouUniversity,Zhengzhou450001，China)

In order to analyze the influence of the structural parameters of the continuous box girder bridge with corrugated steel webs on the self-vibration, the Zhengzhou Longhai Elevated Road Changzhuang reservoir bridge was taken as example, by using ansys software,to build the fine finite element model of the 3 spans continuous bridge. The influence of the structural parameters such as prestressed, angle of the plate, width of the plate and thickness of the web, as well as diaphragm number were all analyzed.Results indicated that the prestressed tension had an stress softening impact to decrease of the total stiffness of the structure. Therefore the vibration frequency of composite box girder with corrugated steel webs was reduced. However, the concrete was in a complex stress state because of prestressed tension,and the elasticity modulus of the material was different from that of the uniaxial stress state. Through revising elastic modulus, the vibration frequency would increase along with the increase of the tensile force. And the results could be consistent with the experimental results. With the increase of the angle of the plate, the vibration frequency was shown to increase at first and then decrease, then there would be a small increase. With the increase of the width, the vibration frequency was shown to increase at first and then decrease. With the increase of the thickness, vertical vibration frequency, longitudinal vibration and torsional frequency all increased, but transverse vibration frequency decreased. The torsional vibration frequency could be obviously increased by increasing the number of diaphragm, but the growth rate of the torsional frequency gradually decreased with the increase of the number of the diaphragm.

structural parameters； composite box girder with corrugated steel webs； continuous girder； vibration frequency

2016-08-25

河南省基础与前沿技术研究项目(162300410264)．

李杰(1974—)，男，陕西宝鸡人，副教授，主要从事桥梁结构理论及力学行为研究，E-mail:lijie2007@zzu.edu.cn.

U442.5

A

1671-6841(2017)01-0120-07

10.13705/j.issn.1671-6841.2016288