噪声对混沌系统检测性能的影响*

石 敏 虢应华 陈晓辉

(1.水声对抗技术重点实验室 湛江 524022)(2.91388部队 湛江 524022)

噪声对混沌系统检测性能的影响*

石 敏1,2虢应华1,2陈晓辉2

(1.水声对抗技术重点实验室 湛江 524022)(2.91388部队 湛江 524022)

理论上,混沌系统具有对噪声不敏感,而对与其内置信号同频率的信号敏感的特点,据此可将混沌系统应用于微弱信号检测。但在实际仿真中发现:当系统处于混沌临界状态,且取精度较高的混沌系统临界阈值时,输入一定功率的白噪声也会引起系统状态的改变,即系统产生虚警。虚警率随着噪声功率的降低而增加,当噪声功率下降到一定值后,虚警率又开始下降,即虚警率存在峰值点。且虚警率与混沌临界阈值的精度有关,临界阈值精度越高,其对应的虚警率越高。

微弱信号检测; 混沌系统检测性能; 噪声; 虚警率

1 引言

混沌系统具有对噪声信号不敏感,而对与之同频率的微弱信号敏感的特点使之能够广泛应用于微弱信号检测中[1～9]。而在实际仿真中发现,当混沌系统处于混沌临界状态时,输入具有不同功率的白噪声,也可能使系统进入到大尺度周期态,从而产生了虚警[10]。

本文仿真在不同精度的临界阈值下,在处于混沌临界状态的系统中,输入具有不同功率的白噪声时系统的性态,分析了噪声对混沌系统检测性能的影响。

2 混沌系统微弱信号检测的基本原理

用于任意频率微弱信号检测的duffing混沌检测系统方程为

(1)

随着γ值的变化,系统的相轨迹将发生变化,当γ等于混沌临界阈值γd时,系统进入混沌临界状态。理论上,在混沌临界状态下若输入纯噪声时,系统仍保持混沌状态,若输入含有与内置信号频率相同的信号时,系统迅速从混沌状态转化为大尺度周期状态,据此可检测微弱信号是否存在。

3 临界阈值的确定

duffing混沌系统微弱信号检测中,混沌临界阈值的确定是至关重要的。利用相轨迹观察法来确定临界阈值易受到仿真时间不够长、人为主观判断等因素影响[11],而采用Lyapunov特征指数可以定量精确确定系统的状态和混沌临界值。其基本思想是:最大Lyapunov特征指数大于零,是系统处于混沌态的标志,当系统最大Lyapunov特征指数由大于零转为小于零,则说明系统从混沌态跃变到了周期态,最大Lyapunov特征指数符号转变的那一刻所对应的内置信号幅度的值就应为系统临界阈值[11]。文献[11]中给出了Lyapunov特征指数的具体计算方法及利用该指数计算系统临界阈值的方法。

图1 最大Lyapunov特征指数与参数γ的关系曲线

表1 11个采样点对应的Lyapunov特征指数值

从图1 可以大致估计出阈值的范围,γd∈[0.82,0.83]。若取混沌临界阈值精度为小数点后两位,则阈值为0.82。若要取更高精度的临界值,可将[0.82,0.83]以0.001为步长进行等分,计算各采样点对应的Lyapunov特征指数,得到表1所示结果。

根据表1可得小数点后取3位的混沌临界阈值为γd=0.825。若要取更高精度的临界阈值,则可将[0.825,0.826]以0.0001为步长进行等分,同样计算各采样点对应的Lyapunov特征指数,根据Lyapunov特征指数值得到更高精度的临界阈值,得到其精度取小数点后4位对应的临界阈值为0.8258。该过程一直持续下去,直到得到预先设置的精度。这里以小数点后8位为设置精度,得到各采样点对应的Lyapunov特征指数如表2所示。

表2 20个采样点对应的Lyapunov特征指数值

由表2可见,小数点后取8位对应的混沌临界阈值为γd=0.82582725。

4 输入不同强度噪声对系统检测性能的影响

当duffing系统处于混沌临界状态时,即式(1)中的γ=γd时,输入不同功率的白噪声,得到方程式:

(2)

式中,γd为混沌临界阈值,σ2为白噪声功率,randn为均值为0,方差为1的高斯白噪声。

以噪声功率为σ2=10-6为例,分别取γd=0.82,0.825,0.8258,0.82582725,每个临界阈值下进行100次仿真实验,得到各仿真中系统对应的最大Lyapunov特征指数如图2所示。

图2 在不同精度临界阈值下,系统输入功率为10-6的白噪声后,系统对应的最大Lyapunov特征指数

定义输入噪声时,系统的虚警率为

(3)

由图2和式(3)可得,在γd=0.82,0.825,0.8258,0.82582725的临界状态下输入功率为10-6的高斯白噪声后,系统对应的虚警率分别为:0%,0%,5%,58%。

表3给出了在不同精度临界阈值下输入不同功率的高斯白噪声后,系统对应的虚警率。

表3 不同精度临界阈值下输入不同功率的白噪声时对应的虚警率

由表3可见,当系统临界阈值精度较低时(如γd=0.82和0.825),噪声不会引起系统的相变,而当临界阈值精度取得较高时,不同功率的噪声导致处于混沌临界状态的duffing系统出现不确定的运动状态,即系统输出可能是混沌状态也可能是大尺度周期状态,因此系统在临界阈值附近对噪声十分敏感,容易出现虚警。

图3给出了当临界阈值分别为0.8258和0.82582725时,在混沌处于临界状态时,输入不同功率的白噪声时,系统对应的虚警率曲线。其中,实线代表γd=0.8258时对应的虚警率曲线,虚线代表γd=0.82582725时对应的虚警率曲线。

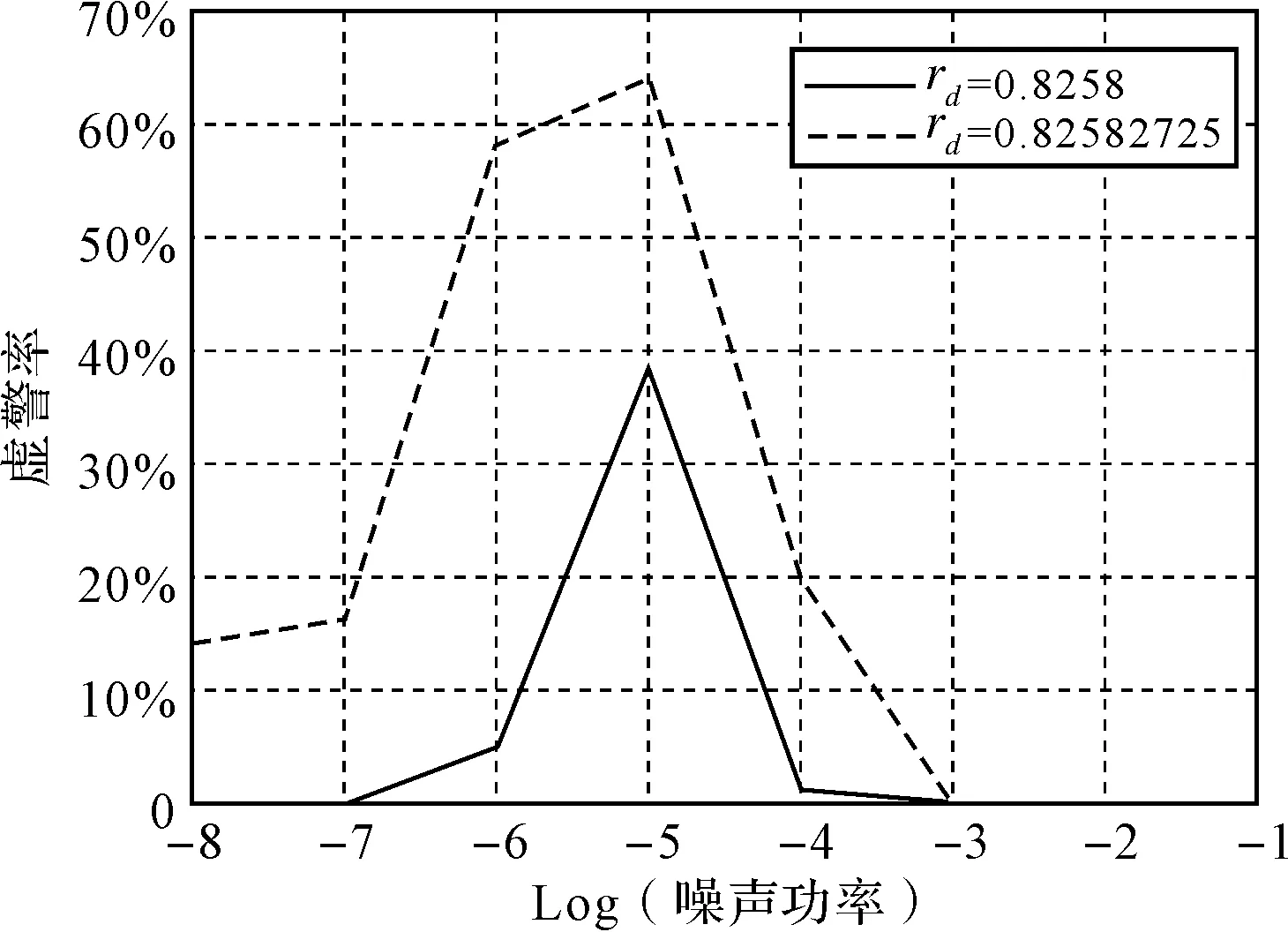
图3 输入不同功率白噪声时对应的虚警率

由图3可见,在临界阈值精度较高时,虚警率随着噪声强度的变化而变化。当噪声强度增大时,系统的无序度增加,越容易进入混沌状态；强度小的噪声具有与周期信号相类似的扰动功能,能够抑制系统的混沌运动。虚警率并不是随着噪声功率减小而单调增加,而是当噪声功率小到一定程度后,虚警率下降,即虚警率存在一个峰值点,推测这是大信号条件下噪声在某个强度时产生了随机共振现象。

5 结语

虽然噪声对混沌系统具有一定的免疫力,但并不是说噪声对系统没有影响。噪声对非线性系统有着不确定性的作用,能使系统产生不同的动力学行为,可以导致混沌或有序[12]。功率较小的白噪声具有与周期信号相类似的扰动功能,起到了抑制系统混沌运动的作用,易使系统进入到大尺度周期态,虚警率增加,而当噪声功率小到一定程度后,无法引起系统状态改变；功率大的噪声对系统的周期分岔具有破坏作用。因此处于混沌临界状态的系统,当取一定精度的临界阈值时,输入纯噪声后系统的虚警率随着噪声功率的降低而增加,当噪声功率降到一定值后,虚警率又开始下降,即虚警率有个峰值点,正如图3所示。

综上所述,混沌临界状态是一种不稳定的状态,不同功率的驱动输入白噪声可能会导致系统状态改变从而产生误判,使系统的检测性能下降。噪声的存在和强弱会影响系统检测微弱信号的能力,因此,随机噪声对系统运动状态的影响是限制混沌微弱信号检测性能的主要原因。但在混沌振子全局分析的基础上,通过对初始值和混沌临界阈值适当选取,可实现一定强度噪声背景下微弱周期信号的可靠检测。

[1] 聂春燕.混沌系统与弱信号检测[M].北京:清华大学出版社,2009,3:6-7.

[2] 陈军.基于混沌理论的检测系统应用研究综述[J].甘肃高师学报,2013,18(2):21-25.

[3] 张刚,胡韬,王颖.基于Melnikov函数Duffing系统微弱信号检测[J].电子测量技术,2015,38(1):109-112.

[4] 桑松.基于小波变换和混沌理论的微弱信号检测方法的研究[D].哈尔滨:东北农业大学,2013:6-7.

[5] 李琳,刘春刚,石硕,等.基于混沌和Lyapunov特征指数的微弱信号检测方法[J].黑龙江大学自然科学学报,2012,29(4):556-560.

[6] JIN Tian, ZHANG Hua. Statistical approach to weak signal detection and estimation using Duffing chaotic oscillators[J]. Science China Information Sciences, 2011,54(11):2324-2337.

[7] 孙文军,芮国胜,张嵩,等.微弱信号混沌检测方法的抗噪性能研究[J].无线电通信技术,2012,38(1):59-62.

[8] 邓宏贵,曹文晖,杨兵初,等.基于混沌理论和小波变换的微弱周期信号检测方法[J].中南大学学报(自然科学版),2012,43(5):1773-1779.

[9] 冉莉,王民.一种强噪声背景下微弱信号检测方法研究[J].信息技术,2012,2:41-45.

[10] 兀旦晖,李秦君,杨萍.噪声对基于Duffing方程弱信号检测的影响[J].计算机测量与控制,2010,18(1):61-63.[11] 张宾. Lyapunov特性指数的算法研究及其在弱信号混沌检测中的应用[D].长春:吉林大学,2004:19-37.

[12] Gan C B. Noise-Induced Chaos in Duffing Oscillator with Double Wells[J]. Nolinear Dynamics.2006,45(3-4):305-317.

Influence of Noise on Detection Performance of Chaotic System

SHI Min1,2GUO Yinghua1,2CHEN Xiaohui2

(1. Science and Technology on Underwater Acoustic Antagonizing Laboratory, Zhanjiang 524022)(2. No.91388 Troops of PLA, Zhanjiang 524022)

Chaotic system has the characteristics that immune to noise and it is sensitive to the signal whose frequency is same as the inner signal’s frequency in a chaotic system in theory. Hereby weak signal hides in strong broad band background noise can be detected by chaotic system. But in the actual simulating process, it finds when choosing critical value of chaotic system with higher precision, pure noise inputs into chaotic system which is under critical state will probably induce to system state variation, namely producing false alarm. The false alarm rate is increasing along with the decreasing of noise power, while the false alarm rate is beginning to decrease when noise power descend to certain value, namely the false alarm rate exists peak value. And the false alarm rate is related to precision of the critical value of chaotic system. The higher precision of the critical value of chaotic system is, the higher the false alarm rate of the chaotic system is.

weak signal detection, detection performance of chaotic system, noise, false alarm rate

TP391

2016年9月9日,

2016年10月17日

石敏,女,博士,工程师,研究方向:水声信号处理技术。虢应华,男,硕士,工程师,研究方向:声纳技术。陈晓辉,男,硕士,助理工程师,研究方向:水声信号处理技术。

TP391

10.3969/j.issn.1672-9730.2017.03.029