数学建模在物流管理专业教学中的应用
2017-04-06曹亚群
曹亚群
(1.合肥工业大学,安徽合肥230009;2.安徽水利水电职业技术学院,安徽合肥231603)
数学建模在物流管理专业教学中的应用
曹亚群1,2
(1.合肥工业大学,安徽合肥230009;2.安徽水利水电职业技术学院,安徽合肥231603)
高等学校的教育目标是为社会培养人才,数学作为公共基础课如何与专业结合,才能更好地提高学生综合素质,是一个值得深入思考的问题.本文研究了数学建模在物流管理中的应用,并进行了典型案例分析.
数学建模;物流管理;高等学校
高等学校开设高等数学是为学生学好专业课做准备,最主要的还是提高学生的数学意识、数学修养,让学生能够运用所学的数学知识解决现实生活中的问题.数学建模刚好是达到这种目的的重要手段之一.近几年,数学建模在高等学校发展很快,笔者从事高等数学教学的同时还兼任学院数模协会指导教师,对数学建模在生活中的应用有着非常深刻的体会.大部分的学生对数学建模都很感兴趣,希望把学习的高等数学知识应用到专业技能中去.因此,数学建模教学应根据各专业的不同而有所变化,本文主要对数学建模在物流管理中的应用进行一些探讨.
1 什么是数学建模
数学建模是通过相关数学方法、数学思想和数学方面知识的运用,来解决现实生活中的实际问题,通过对问题的数学化建立数学模型,并对这个模型进行求解,将求解结果应用于实际问题,检验数学模型的正确与否,从而根据检验结果对模型进行修正,如此循环多次,直到所建立的数学模型能准确地反映出现实问题的直接特征.数学建模可以把数学方面的理论知识和现实生活中的实际问题联系起来,从而解决实际问题[1].
数学建模主要有两种:一是根据事物规律和本质的理论分析,也就是应用数学工具对事物的客观内在联系进行简化,描述出对象特征的数学模型.二是根据计算或测试具体数据得出的实验归纳,用数据统计及数学理论等归纳的数学模型.建模过程如下:
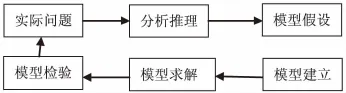
2 数学建模在物流管理中的应用
物流管理主要包括:1、对物流系统各要素的管理,如设备、信息等.2、对物流活动各要素的管理,如存储、运输等.3、对物流活动各职能的管理,如技术、质量等,物流管理涉及电子商务、企业管理、市场营销等多个学科.现代物流中遇到的实际问题,可以通过建立数学模型来解决.比如:储存货物如何占地空间最少?如何选址建立仓库,使运输费用最少?工厂如何生产才能使利润最大?快递公司怎样安排路线,才能使运营成本最低等[2].
问题一:某个企业生产了甲、乙、丙三种产品,生产过程中所使用和消耗原料A和原料B、所生产的产品单件利润值和库存原料数如表1所示[3],求解甲、乙、丙三种产品应各生产多少件时,该企业的利润最大?

表1 原料、利润和库存情况
分析:建立相应的数学模型:
设甲、乙、丙三种产品生产x1、x2、x3件时,该工厂的利润最大.

在具体工作中,把已知数据代人数学模型并用数学软件LINGO或MATLAB运算,从而求得最大利润.
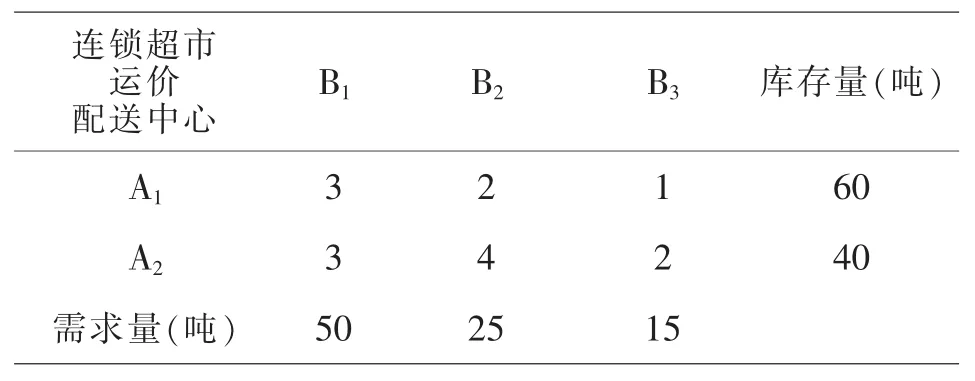
表2 配送中心库存量、各连锁超市需求量以及每吨运费
问题二:现从两个配送中心运送商品到三个连锁超市,配送中心的商品库存量、三个连锁超市的需求量以及每吨商品的运费见表2.试问应采取哪种运输方案时,总运费最少?
分析:建立相应的数学模型:
设xij表示配送中心Ai运往连锁超市Bj的商品数量(i=1,2;j=1,2,3)则
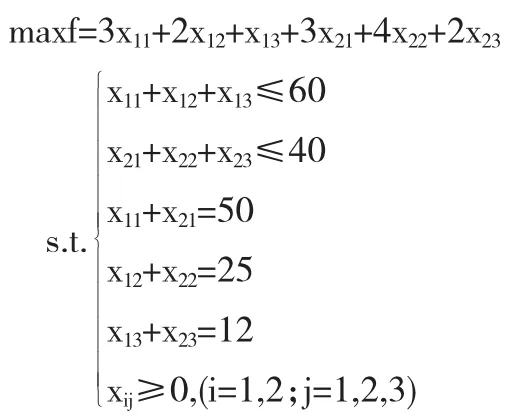
问题三:火龙果的运价及产销量如表3,应采用哪种方案,才能使总运费最少?

表3 运价产销量
分析:建立相应的数学模型:设xij表示产地Ai(i=1,2)供给销地Bj(j=1,2,3)的物质数量.
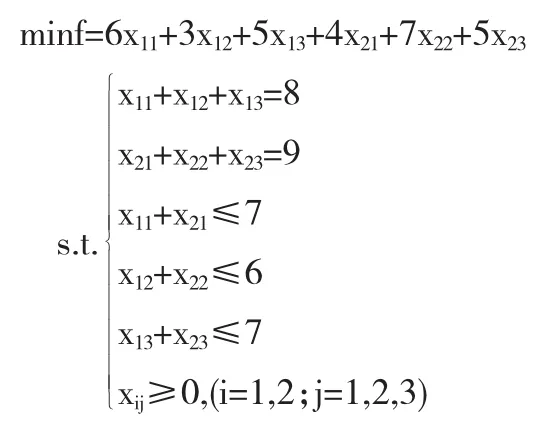
问题四:某大型企业生产一种产品[4],从A1,A2,A3三个产地购进原材料20吨,45吨,50吨,然后再把这些原材料运输到B1,B2,B3三个分厂,它们的需要量分别是25吨,40吨,35吨,从产地到各分厂的运价见表4,试问怎样安排调运,总运费最少?

表4 运价表(单位:元/吨)
分析:建立相应的数学模型:
设从产地Ai(i=1,2,3)到Bj(j=1,2,3)的调运量为xij(i=1,2,3;j=1,2,3)
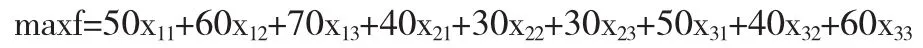

问题五:某快递公司从车站向公司总部每天要运输至少150吨的快递,该快递公司有8名驾驶员,拥有3辆A型卡车和6辆B型卡车,载重量分别为9吨和7吨,A型卡车成本每辆每天往返需要450元,B型卡车成本每辆每天往返则需要325元,A型卡车和B型卡车每天可分别可以往返4次和5次[5],见表5.问该快递公司如何安排车辆,运营成本最低?

表5 车型车况表
分析:建立相应的数学模型:
设安排A型卡车和B型卡车分别为x1、x2辆时,运营成本最低.

3 小结
数学建模在物流管理中有广泛的应用,通过建立数学模型解决物流管理中出现的一些问题.对物流管理专业进行数学教学时,渗入数学建模的知识,将物流专业具体问题引入课堂中,用数学理论知识解决物流管理问题,丰富课堂教学,引导学生分析实际问题.从而思考出对应的解决方案,提高学生解决问题的能力,拓展学生的思维空间,培养学生探索和创新能力,提高学生的专业素质.
〔1〕王志琦.探究数学建模思想在数学教学中运用[J].内蒙古师范大学学报(教育科学版),2013,26(6):141-143.
〔2〕梅峰太.以物流管理专业为例浅谈高等学校数学建模与专业学习结合[J].时代教育,2011(11):135-136.
〔3〕徐敏.数学软件MATLAB在物流管理中的应用[J].中国商贸,2013(21):122-123.
〔4〕刘敏.物流管理概论[M].上海交通大学出版社,2005.
〔5〕曾琢.线性规划法在物流管理中的应用[J].中国市场,2015(7):24-25.
G642
:A
:1673-260X(2017)03-0214-02
2016-12-12
