半主动空气悬架的神经模糊控制

江 洪，王子豪，孔 亮

(江苏大学 机械工程学院，江苏 镇江 212013)

半主动空气悬架的神经模糊控制

江 洪，王子豪，孔 亮

(江苏大学 机械工程学院，江苏 镇江 212013)

以带附加气室容积可调空气悬架的整车为研究对象，首先建立附加气室容积可调空气弹簧模型，并将该模型以弹簧力形式引入整车，然后设计以平顺性指标为主导地位的综合目标函数及约束条件。采用改进遗传算法对该目标函数进行逐段优化，同时得到不同工况下前悬架和后悬架模糊控制器的最优输出数据。最后将该输出数据作为导师信号供神经网络学习，从而建立整车半主动空气悬架的T-S型神经模糊控制器。仿真结果表明：在不同行驶工况下，相比被动空气悬架，采用神经模糊控制的半主动空气悬架的行驶平顺性显著提高，且满载时的改善效果优于空载。

附加气室；空气悬架；神经模糊控制；改进遗传算法；平顺性

将空气弹簧和容积可调附加气室通过管路和电磁阀连接就构成了新型的附加气室容积可调空气弹簧。通过电磁阀的通断可实现不同容积附加气室和空气弹簧的选择性联通，从而达到调节弹簧刚度的目的。传统的空气弹簧无附加气室，刚度不可调。对车辆系统而言，不同的工况对弹簧刚度的要求不同，附加气室容积可调空气悬架可以很好地适应这种工况变化，提高车辆的行驶平顺性。带有附加气室容积可调空气弹簧的悬架系统刚度调节效果好、控制方便、可靠性高，无疑是一种性能优良的半主动空气悬架系统[1]。

2009—2012年，王家胜、朱思洪、李美等[2-4]深入研究了带附加气室空气悬架的工作机理，获得了空气悬架静刚度、动刚度随附加气室容积的变化规律，这为开展附加气室容积可调空气悬架控制方法的研究提供了条件。2014年，孔亮等[5]利用遗传算法得到不同工况下的最优附加气室容积值，并在此基础上设计了1/4车附加气室容积可调空气悬架的决策控制器，但该决策控制器建立在对行驶工况准确辨识的基础上，局限性较大，且1/4车辆模型并不能完全反映整车的振动情况。2015年，江洪等[6]设计了整车附加气室容积可调空气悬架的Mandani型模糊控制器，取得了一定的控制效果。但受控制算法本身局限性的影响，在生成模糊规则及调整隶属函数时无可避免地存在较强的主观性，且并未兼顾前后悬架附加气室容积控制的协同问题。2016年，李重重[7]提出一种适用于悬架刚度控制的动态迭代跟踪控制算法，并将其用于附加气室容积控制，其控制特点是使悬架性能在一段时间内逐渐趋近于最优，但这一过程耗时较长，不适应于路面条件多变的行驶工况。

本文构建了以平顺性为主导地位的综合目标函数，并采用改进遗传算法对该目标函数进行优化，从而得到整车模糊控制器在不同行驶工况下的最优输出数据。再利用神经网络自学习功能对得到的最优输出数据不断训练学习。之后自动生成模糊控制规则及隶属函数，该方法减少了大量人为繁琐的操作，进一步提高了车辆在多工况下的行驶平顺性。

1 整车空气悬架模型

1.1 附加气室容积可调空气弹簧模型

空气弹簧在垂向激励力F1作用下发生变形，簧上质量m在动态空气弹簧力F的作用下产生垂向位移Z。此时空气弹簧与附加气室中的气体质量通过连接管路相互交换，附加气室接入空气弹簧的容积可通过电磁阀调节。附加气室容积可调空气弹簧作为空气悬架系统的核心部件，建立其精确的数学模型对于研究悬架系统意义重大。附加气室容积可调空气弹簧模型如图1所示。

图1 附加气室容积可调空气弹簧模型

空气弹簧力中密封的压缩空气形成了动态弹簧力F，其表达式如下：

(1)

式中：P1为空气弹簧内气体的绝对压力；P0为大气压；Ae为空气弹簧截面积。

在外界激励F1作用下，空气弹簧和附加气室内的气体通过连接管路形成对流，此时空气弹簧可视为开口系统，且内部气体质量在不断变化。由于气体质量很小，可以忽略气体的重力势能和动能，因此空气弹簧的存储能只有热力学能，系统内气体可近似等同于绝热状态。根据热力学第一定律可得空气弹簧内气体的能量守恒方程[8]：

0=dU1+dH1+dW1

(2)

空气弹簧热力学能增量表示为

dU1=d(m1cvT1)=cv(T1dm1+m1dT1)

(3)

式中：m1为空气弹簧内气体质量(kg)；cv为定容比热容(J/(kg·K))；T1为空气弹簧内气体温度(K)。

当气体通过连接管路流出空气弹簧时，因气体流动而转移的能量为

dH1=-cpTdm1

(4)

式中：cp为空气的定压比热容(J/(kg·K))；T为连接管路中流动空气的温度(K)。当气体从空气弹簧流进附加气室时，T等同于空气弹簧内气体温度；当气体从附加气室流入空气弹簧时，T等同于附加气室内气体温度。

弹簧通过伸缩变形对外做功，其表达式如下：

dW1=P1dV1

(5)

式中：P1为空气弹簧内气体的绝对压力(Pa)；V1为弹簧容积(m3)。

将式(3)～(5)代入式(2)进行计算并化简，最终可得空气弹簧内气体绝热状态方程：

(6)

附加气室和空气弹簧通过管路连接，两者内部气体状态类似，因此附加气室内气体状态的推导过程同空气弹簧，其表达式为

(7)

式中：P2为附加气室内空气绝对压力；V2为附加气室容积；m2为附加气室内气体质量。

附加气室容积可调空气弹簧系统建模的关键是如何建立连接管路中流动气体的质量流量关系式。连接管路中气体的流量特性和弹簧系统的动态特性密不可分。主附气室连接管路的简化模型如图2所示。其设计思想为：将管路微分为无数个ds长度的微元管路(如图2中阴影部分)，无数个微元管路串联后就形成了连接管路模型。

图2 连接管路模型

将连接管路中流动气体的动态参数表示为管路长度s和时间t的函数，建立管路流量特性守恒方程组，最后通过偏微分方程简化求解该守恒方程组，获得连接管路中气体质量流量表达式[9]：

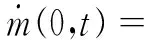
(8)

式中：Rg为管路摩擦阻力系数；Se为连接管路的有效流通面积；Pmax为连接管路两端压力较高一端的压力值；Pmin为连接管路两端压力较低一端的压力值；P1、P2为连接管路两端的气压；T为交换空气的温度，其值等于Pmax端的空气温度。

1.2 整车悬架模型

传统建模过程习惯将空气弹簧作为定刚度的对象进行考虑，但实际的研究结果表明：空气弹簧具有很强的非线性，其弹簧刚度随着空气弹簧位移的变化而变化。因此，本文将附加气室容积可调空气弹簧模型以弹簧力的方式引入整车悬架模型，从而减小实际的建模误差。带附加气室容积可调空气弹簧的整车模型如图3所示。

假设4个悬架、座椅和车身连接处的作用力和垂直位移分别为Fi、Fc、Zi0、Zc0，对簧下质量、车身和座椅分别运用牛顿运动学可得其运动方程：

(9)

其中：mcb、mb分别为车身和座椅质量；Zcb为整车质心位置处的垂直位移；Zc为整车后排座椅处垂直位移；Kc、Cc分别为座椅的刚度和阻尼系数；Jx、Jy分别为车身侧倾和俯仰转动惯量；θ、φ分别为车身侧倾和俯仰角位移；lf、lr分别为前后轮至车身质心横轴的水平距离；d为左右车轮轮距；Fei、Ci分别为可控弹簧力(由附加气室容积调节)和减振器阻尼系数(i=1～4)。

图3 带附加气室容积可调空气弹簧的整车模型

2 神经网络训练数据采集

神经网络需要优秀的导师信号作为学习对象才能建立模糊控制器。导师信号是控制系统的最优输出量，因此获得导师信号的过程即为寻求全局最优的过程。

遗传算法(genetic algorithm， GA)按照优胜劣汰的法则对待求问题的解空间进行全局搜索，可快速收敛至最优解[10-11]。建立被控对象的优化目标函数及约束条件是采用改进遗传算法对输出量进行优化的前提，然后在此基础上利用该算法得到车辆在不同工况下前悬架和后悬架的最优附加气室容积值，并将该数据作为导师信号供神经网络学习。

2.1 遗传算法综合目标函数的确定

遗传算法优化得到的输出量用于训练神经网络得到模糊推理系统，因此遗传算法的目标函数可看作整车悬架系统的控制目标。对于整车而言，本文建立的目标函数囊括了座椅加速度、质心加速度、悬架动行程、轮胎动载荷，并同时兼顾侧倾角加速度及俯仰角加速度。目标函数为关于这几个指标的加权和，表达式如下：

(10)

对于整车而言，fF、fR、FF、FR均包含左右两侧的量，且整车的结构左右对称，左右车轮的实际路面激励相似，因此在目标函数中的权重系数前各自乘以2。

在进行优化计算时可以考虑逐段优化。逐段优化的子目标函数为J(t)的均方根值在某一小段时间内是否减小，以此为依据来判断悬架性能是否改善。J(t)的均方根值表达式为

(11)

最终可得到各个不同时间段内的多组优化数据，以此数据进行训练学习得到的控制系统，其控制过程更加细腻，控制效果更加显著。在直线行驶工况下主要考虑改善车辆行驶平顺性，因此目标函数中加速度起主导地位，故将这8项指标的重要性比重定为：

n1∶n2∶n3∶n4∶n5∶n6∶n7∶n8=

15∶15∶1∶1∶1∶1∶1∶1

假设：车身载荷为满载；设置A级路面80 km/h白噪声激励；仿真时间为10 s；采样频率为100 Hz。仿真结束后得到目标函数中8项指标各1 000个数据，各自均方根值计算结果如下：

其他路面等级和车速同理计算。综合8项指标的目标函数，不仅重点考虑了车辆的行驶平顺性，同时兼顾了车辆的操纵稳定性，能全面反映车辆悬架的综合性能。

2.2 遗传算法设计变量及其范围的选取

本文主要考虑在空气弹簧上连接附加气室后，如何通过改变附加气室容积来调节悬架刚度、提升悬架综合性能。研究对象为亚星YBL6891型客车。其前悬架单侧包括1个空气弹簧、1个附加气室；后悬架单侧包括2个空气弹簧、2个附加气室。因此，分别选择前悬架和后悬架的附加气室容积作为优化设计变量。由于后悬架单侧的2个空气弹簧参数及状态完全相同，因此可以假设这2个空气弹簧配备的附加气室容积相等。假设后悬架单侧的两个附加气室容积分别为Va21、Va22，则Va21=Va22=Va2。设计变量为

(12)

式中：Va1为与前悬架空气弹簧匹配的附加气室容积(L)；Va2为与后悬架空气弹簧匹配的附加气室容积(L)。

大量特性试验研究结果表明：当附加气室的容积达到空气弹簧容积的1.5倍时，附加气室调节空气弹簧刚度的能力已变得十分微弱。本研究对象所配备的空气弹簧容积约为9.6 L，因此将前悬架和后悬架附加气室的容积均设置为0～14 L[9]。

2.3 约束条件的建立

为保证车辆实际行驶过程中的实用性及安全性，本研究根据相关参考文献对整车前后悬架的设计变量进行必要的约束。根据车辆行驶时的具体情况，主要有以下2项约束条件[12]：

1) 悬架动行程的大小将直接影响车身撞击限位块的概率，该值过大会严重影响车辆的行驶平顺性，通常对于客车其许用行程[fd]为5～8 cm。将动行程的约束条件设置为RMSf≤[fd]/3时，则车身撞击限位块的概率<0.3%。

2) 车辆行驶安全性受轮胎相对动载荷F/G影响较大。当该值过大时，车轮脱离地面的概率增加，严重影响车轮与地面附着力。如果将整车所有位置处轮胎相对动载荷的约束条件设置为RMSF/[G]≤1/3，可大大提高车轮与路面之间的附着力，确保车轮脱离地面的概率<0.15%[12]。

2.4 改进遗传算法及其运算流程

基本遗传算法没有采取对优良个体的保护措施，使得遗传操作中的交叉算子及变异算子破坏优良个体的可能性增加。

采用“最优保存策略”对基本遗传算法进行改进：首先在每一代父代种群中选择一定比例的优秀个体直接进入下一代，其余个体参与遗传操作产生新个体，然后用这些新个体淘汰父代种群中较差的个体，最后将直接进入下一代的优秀个体和新子代个体组成父子混合新种群，并按照这种方式反复迭代。改进遗传算法有效避免了交叉及变异算子对种群中优秀个体的破坏，可将优良个体进行世代保存，使得进化群体一代更比一代优秀，极大提高了算法的搜索效率。运算流程如图4所示。

2.5 神经网络训练数据采集

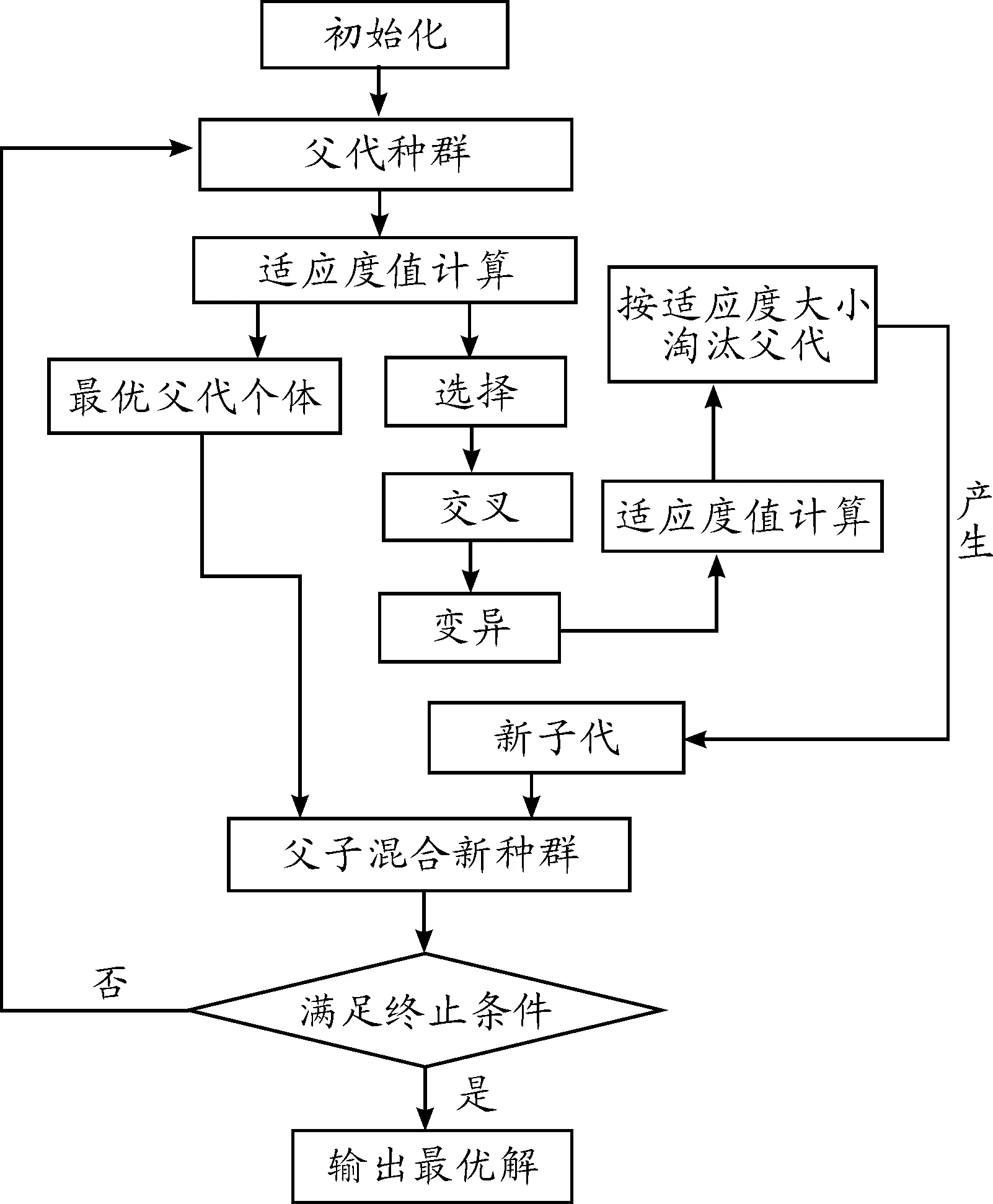
图4 改进遗传算法运算流程

图5 被控系统输出量数据采集原理

客车常用路面等级及对应的行驶车速为：A级路面对应车速80 km/h；B级路面对应车速60 km/h；C级路面对应车速40 km/h。采样时间为10s，采样频率为100 Hz，逐段优化周期设置为2 s。考虑车身空载和满载两种情况，最终得到每个工况下前悬架和后悬架最优附加气室容积值的5组数据。表1为满载、A级路面、车速为80 km/h时(简称为满载A80工况)前悬架和后悬架附加气室容积在不同时段内的最优值。

表1 满载、A级路面不同时段内的最优容积值

由表1可知：在满载A80工况下、0～2 s的时间段内，当前悬架附加气室容积Va1取5.6 L、后悬架附加气室容积Va2取14 L时可确保式(10)的综合目标函数值在该时间段内取得最小值；在2～4 s的时间段内，当前悬架附加气室容积Va1取5.1 L、后悬架附加气室容积Va2取14 L时可确保式(10)的综合目标函数值在该时间段内取得最小值。其余时间段同理分析，最终可确保式(10)的综合目标函数在该工况下的每个时间段内均取得最小值，即目标函数最优。其余工况同理分析。采用分段优化所得到的最优输出数据进行训练学习得到的控制系统，其控制过程更加细腻，控制效果更加显著。

3 神经模糊控制器设计

3.1 神经模糊控制器的结构设计

整车前悬架包括2个带附加气室容积可调的空气弹簧(左右侧各1个)，后悬架包括4个带附加气室容积可调的空气弹簧(左右侧各2个)，因此本文采用6个二维模糊控制器对整车前后悬架分别进行控制。整车左右两侧的路面激励及车身结构类似，因此左右两侧的附加气室容积可调空气弹簧系统可共用1个控制器。后悬架单侧的两个空气弹簧的参数及状态完全相同，附加气室容积取值相同，因此后悬架单侧的2个模糊控制器可采用相同设计。二维模糊控制器的输入量分别为对应悬架的轮胎动载荷及空气弹簧气压，其中轮胎动载荷用于感知路面变化，空气弹簧气压用于感知车身载荷的变化。输出量为附加气室容积。整车模糊控制器的结构设计如图6所示。

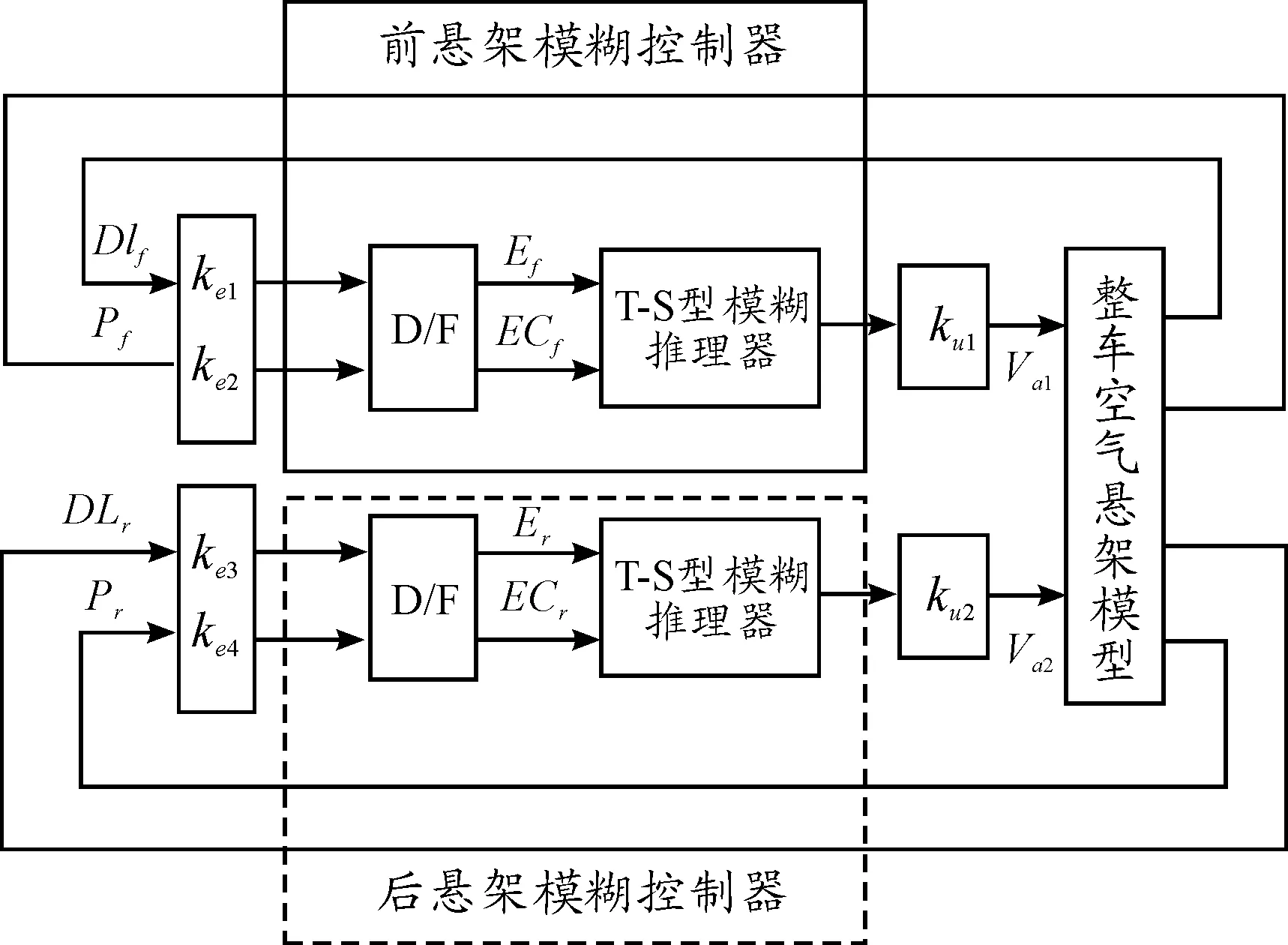
图6 整车模糊控制器结构设计

由图6可知：前悬架模糊控制器的输入分别为前悬架轮胎动载荷DLf、前悬架空气弹簧气压Pf，这2个输入量经过量化因子ke1、ke2及模糊化模块D/F后得到模糊变量Ef和ECf，再经过T-S型模糊推理器及比例因子ku1后得到驱动执行机构的清晰量Va1。后悬架模糊控制器类似。

3.2 T-S型神经模糊推理系统的建立

采用自适应神经网络模糊推理系统(Anfis)对采集的训练数据进行学习，从而自动生成模糊控制系统的隶属函数及模糊规则，省去了人为调整隶属函数及编制模糊控制规则等繁琐过程，提高了控制精度[13-14]。在Matlab中调出T-S型模糊推理系统FIS。由于模糊控制器为双输入单输出系统，因此在默认基础上增加一个输入。将前悬架的2个输入分别命名为DLf、Pf，输出命名为Va1。模糊逻辑运算中的“与”算法取求积，“或”算法取代数和，“清晰化”算法取加权平均[11]。完成设计后的前悬架T-S模糊推理系统如图7所示。

通过前悬架的T-S型模糊推理系统的“编辑”菜单调出该系统的自适应神经网络模糊推理系统(Anfis)，将前悬架采集到的训练数据进行装载，采用网格划分法生成初始FIS。覆盖2个输入量的隶属函数均选择高斯函数，模糊子集个数均选择5[16]，输出量采用线性形式。最终生成一个带有25条模糊控制规则的初始FIS。系统Anfis结构如图8所示。

图7 前悬架T-S型模糊推理系统

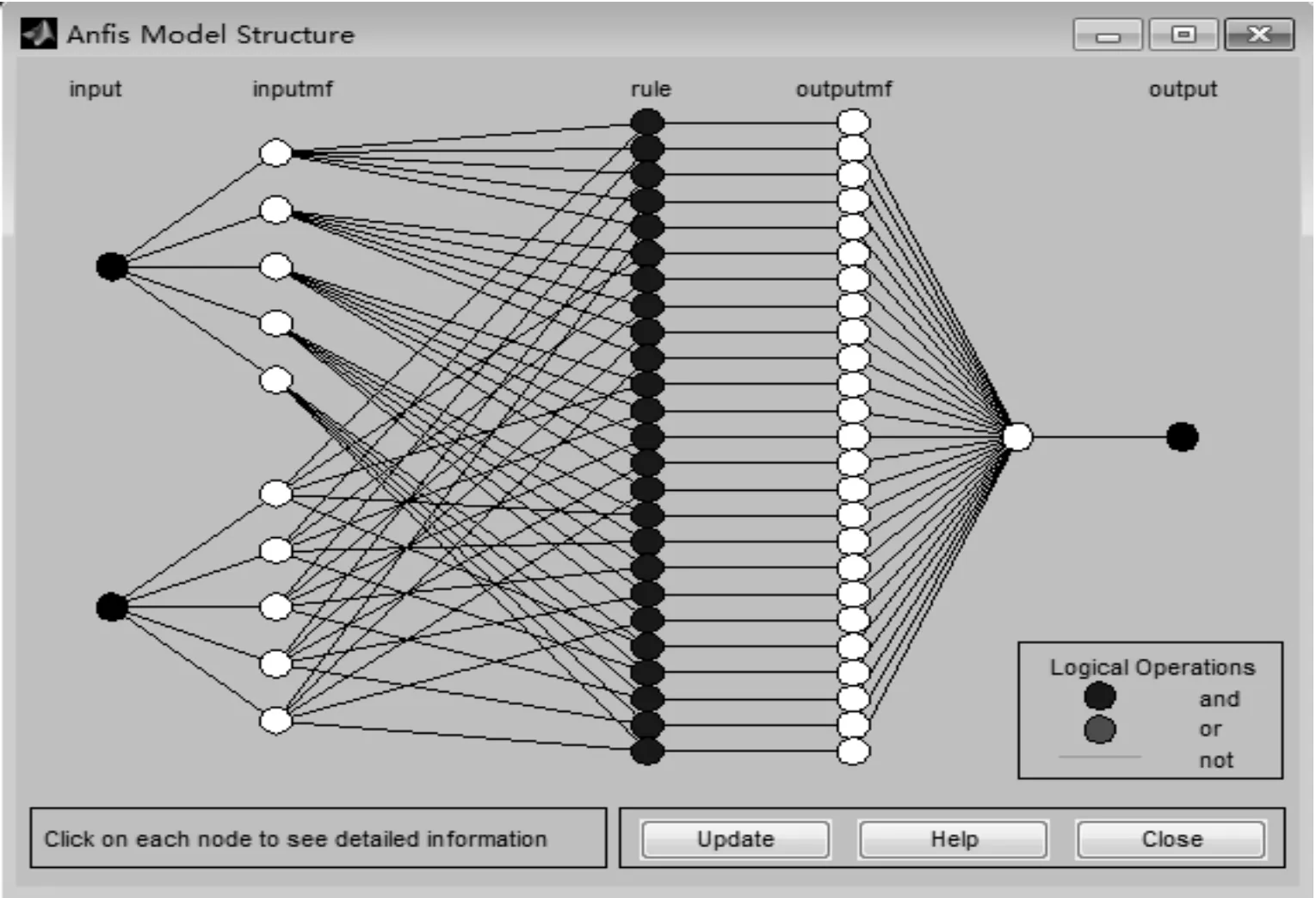
图8 前悬架T-S型模糊推理系统的Anfis结构

在初始FIS的基础上采用混合法对前悬架的神经网络进行训练，此训练过程可以自动调节隶属函数的分布情况，但不改变其类型。当训练次数达到15次后，训练误差趋于稳定，结束训练。神经网络的训练过程如图9所示。

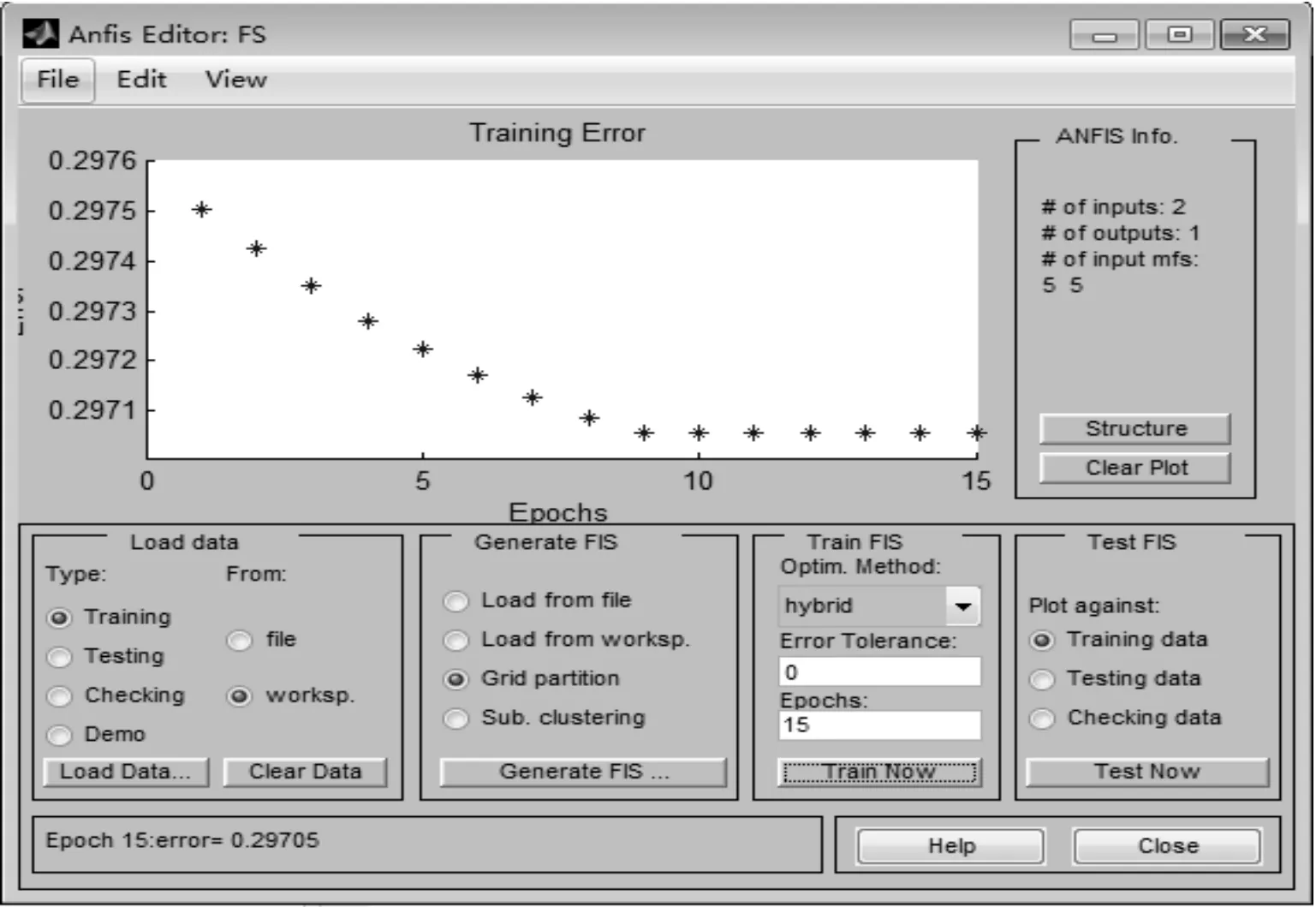
图9 前悬架输出量的训练过程

前悬架通过训练后的输出和改进遗传算法优化得到的输出之间的误差关系如图10所示。训练结束后显示前悬架的平均训练误差为0.297 05，其中：红色星号点为训练的输出数据，蓝色圆圈点为改进遗传算法优化得到输出数据。

图10 前悬架数据对比测试

最终可得前悬架2个输入量的隶属函数分布，如图11所示。

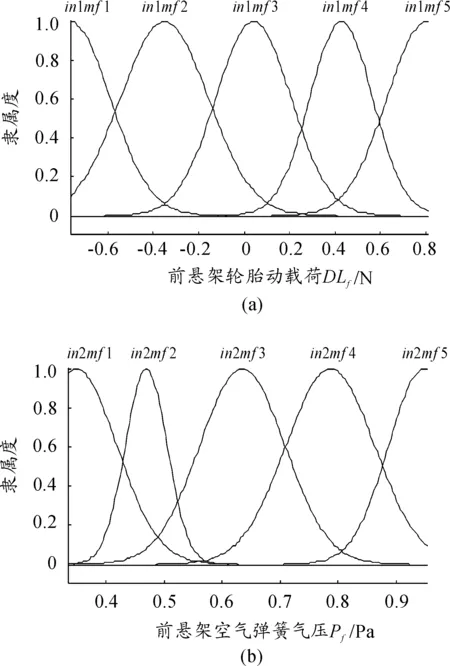
图11 前悬架2个输入量的隶属函数分布

后悬架的T-S型模糊推理系统同理设计。

4 神经模糊控制器仿真分析

现将上述建立的前悬架及后悬架模糊推理系统分别嵌入整车悬架的模糊控制器中。其中，前左悬架模糊控制系统仿真模型如图12所示，其余悬架的仿真模型结构与此类似[17]。整车仿真参数如表2所示[18]。

图12 前左悬架模糊控制系统仿真模型

参数名称数值车身质量(满载)/kg9560车身质量(空载)/kg6520座椅质量/kg25座椅刚度/(N·m-1)36400座椅阻尼系数/(N·(s·m-1))570前悬架非簧载质量/kg415后悬架非簧载质量/kg825前悬架减振器阻尼系数/(N·(s·m-1))9900.45后悬架减振器阻尼系数/N·(s·m-1)9378.29前悬架轮胎刚度/(kN·m-1)650后悬架轮胎刚度/(kN·m-1)1300

为验证神经模糊控制器的有效性，将整车半主动悬架和被动悬架在相同路面激励下进行时域和频域响应的对比分析，并采用改进遗传算法的综合目标函数J(t)作为整车半主动悬架和被动悬架的行驶平顺性评价函数。

整车前后轮均采用A级路面白噪声输入，行驶车速为80 km/h，其中对前、后轮设置关于车速的时间差，车身载荷为满载。半主动悬架和被动悬架的时域及频域响应的仿真对比结果如图13所示。

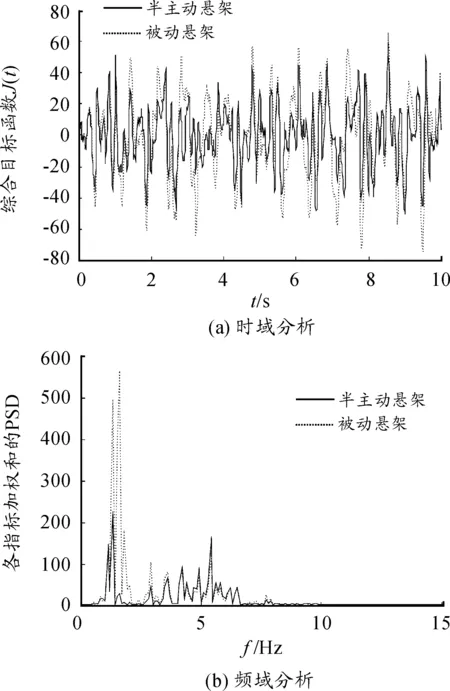
图13 满载、A级路面综合指标加权和对比

由于综合目标函数值包含正负，因此采用均方根值和峰值对综合目标函数进行处理统计，其计算结果如表3所示。

表3 满载、A级路面综合目标函数均方根值及峰值对比

由表3知，相对于被动空气悬架，半主动空气悬架对于以平顺性指标为主导地位的综合目标函数的均方根值及峰值改善效果显著，车辆的平顺性得到有效提升。由图13(b)的频域分析可知，半主动空气悬架相比于被动空气悬架在1～3 Hz频域区间内的振动能量均得到改善，尤其在1.3、1.6、2.9 Hz左右处的振动能量峰值得到有效抑制，而在5.4 Hz左右处的振动能量峰值略有恶化，其余频段内的曲线较为吻合。

在与上述相同的路面等级激励及车速下，考虑车身载荷为空载，半主动悬架和被动悬架的仿真对比及统计结果如图14及表4所示。

图14 空载、A级路面综合指标加权和对比

由表4可知：半主动空气悬架相对于被动空气悬架的综合目标函数的均方根值及峰值均有所改善；图14(b)的趋势和图13(b)类似，但是半主动空气悬架相对于被动空气悬架在1.3、1.6、2.9 Hz左右处的振动能量峰值的抑制效果不如满载时，并且在5.4 Hz左右处的振动能量峰值恶化程度高于满载。其余工况可同理分析。

5 结论

1) 以平顺性为主导地位的综合目标函数作为控制系统的评价函数时，相对于被动空气悬架，采用神经模糊控制的半主动空气悬架有效提升了整车在不同路面等级下的行驶平顺性。

2) 采用神经模糊控制的半主动空气悬架相对于被动空气悬架在1～3 Hz频域区间内的振动能量改善效果显著，而在5.4 Hz左右处的振动能量略微恶化，其余频域区间的振动能量较为吻合，在10～15 Hz频域区间内的振动能量几乎一致。

3) 在相同路面等级及车速激励下，对比分析满载及空载时的数据表及频域图可知：满载时半主动空气悬架对于综合目标函数的改善效果明显优于空载时，这说明采用神经模糊控制的半主动空气悬架对于提升重载车辆的平顺性更具潜力，同时验证了本文所采用的改进遗传算法的优化及神经网络的学习是有效果的。

[1] ADRIAN W.Novel Semi-Active Suspension with Tunable Stiffness and Damping Characteristics[D].Waterloo,Ontario,Canada：[s.n.],2012.

[2] 王家胜，朱思洪.带附加气室空气弹簧动刚度的线性化模型研究[J].振动与冲击,2009(2):72-76，201-202.

WANG Jiasheng,ZHU Sihong.Linearized model for dynamic stiffness of air spring with auxiliary chamber[J].JOURNAL OF VIBRATION AND SHOCK,2009(2):72-76,201-202.

[3] 王家胜，朱思洪.带附加气室空气弹簧动刚度影响因素试验研究[J].振动与冲击,2010(6):1-3,20,231.

WANG Jiasheng,ZHU Sihong.Experimental study on influential factors on dynamic stiffness of air spring with auxiliary chamber[J].JOURNAL OF VIBRATION AND SHOCK,2010(6):1-3,20,231.

[4] 李美.带附加气室空气弹簧系统动态特性机理的研究[D].镇江：江苏大学,2012.

LI Mei.Mechanism Analysis on Dynamic Characteristics of Air Spring System with auxiliary chamber[D].Zhenjiang:Jiangsu University,2012.

[5] 孔亮，江洪，徐兴.附加气室容积可调空气悬架系统的决策控制[J].机械设计与制造，2014(5):246-294.

KONG Liang,JIANG Hong,XU Xing.Decision-Making Control of Air Suspension with Adjustable Auxiliary Chamber[J].Machinery Design & Manufacture，2014(5):246-294.

[6] 江洪，钱宽，孔亮，等.附加气室容积可调空气悬架模糊控制研究[J].重庆理工大学学报(自然科学)，2015(10):29-33.

JIANG Hong,QIAN Kuan,KONG Liang，et al.Study on Fuzzy Control Applied in Adjustable Volume Air Suspension with Additional Air Chambers[J].Journal of Chongqing University of Technology(Natural Science),2015(10):29-33.

[7] 李重重.附加气室容积可调空气悬架刚度和阻尼控制[D].镇江：江苏大学,2016.

LI Chongchong.Stiffness and Damping Control of Air Suspension with Adjustable Volumes of Auxiliary Chamber[D].Zhenjiang:Jiangsu University,2016.

[8] 沈维道，童钧耕.工程热力学[M].北京：高等教育出版社,2007.

SHEN Weidao,TONG Jungeng.Engineering Thermodynamics[M].Beijing:Higher Education Press,2007.

[9] 王家胜.带附加气室空气弹簧动力学特性研究[D].南京：南京农业大学，2009.

WANG Jiasheng.Research on Dynamic Characteristics of Air Spring with Auxiliary Chambers[D].Nanjing:Nanjing Agricultural University,2009.

[10]雷英杰，张善文.Matlab遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2011.

LEI Yingjie,ZHANG Shanwen.The Application and Toolbox of Genetic Algorithm Based on Matlab[M].Xi’an:Xidian University Press,2011.

[11]徐志强.基于改进遗传算法的汽车主动悬架模糊控制研究[D].邯郸：河北工程大学，2011.

XU Zhiqiang.Studying of Fuzzy Logic Control for Vehicle active Suspension Based on Improved Genetic Algorithm[D].Handan:Hebei University Of Engineering,2011.

[12]余志生.汽车理论[M].5版.北京：机械工业出版社，2009.

YU Zhisheng.Automotive theory[M].5 Edition.Beijing:China Machine Press,2009.

[13]SEBASTIAN K,MAREK P.Fuzzy Control for Semi-Active Vehicle Suspension[J].Journal of Low Frequency Noise 2014(4):323-328.

[14]LIAN R J,LIN B F,SIE W T.Self-organizing fuzzy control of active suspension systems[J].International Journal of Systems Science,2005(2):363-369.

[15]刘亚骄.基于自适应神经模糊控制的汽车半主动悬架系统仿真分析[D].西安：长安大学，2014.

LIU Yajiao.Study on Mathematical Model and Adaptive Neuro-fuzzy Control of Semi-active Suspension[D].Xi’an:Chang’an University,2014.

[16]石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京：清华大学出版社，2008.

SHI Xinmin,HAO Zhengqing.Fuzzy control and its simulation of MATLAB[M].Beijing:Tsinghua University Press,2008.

[17]李恩科, 宋礼, 樊成程,等. 客车空气悬架行驶动力学分析与优化[J]. 客车技术与研究, 2015(4):27-30.

LI Enke，SONG Li，FAN Chengcheng，et al. Analysis and Optimization on Coach Air Suspension’s Running Dynamics[J]. Bus & Coach Technology and Research, 2015(4):27-30.

[18]杨启耀.ECAS客车悬架系统的匹配与充放气研究[D].镇江：江苏大学，2008.

YANG Qiyao.Research on Matching and Inflation/Deflating of Suspention System in ECAS-Bus[D].Zhenjiang:Jiangsu University,2008.

(责任编辑 刘 舸)

Neural-Fuzzy Control Applied in Adjustable Volume Air Suspension with Additional Air Chambers

JIANG Hong，WANG Zi-hao，KONG Liang

(School of Mechanical Engineering, Jiangsu University, Zhenjiang 212013, China)

We studied on a whole vehicle equipped with adjustable volumes air suspension, firstly, a model of adjustable volumes air spring with additional air chamber was established, and then the model was substituted into a whole vehicle model in the form of the spring force. Secondly, we designed comprehensive objective function which regard the ride comfort indicator as leading status, and then the function of the whole vehicle was optimized cycle by cycle by the GA (genetic algorithm) to receive the optimized output data of the fuzzy controller of front suspension and rear suspension under different driving conditions and then processed the data for learning of neural network to establish the T-S neural fuzzy inference systems. The results show that the semi-active air suspension with fuzzy controller compared with the passive air suspension improved the ride comfort significantly under different driving conditions, and the improved effect was superior to vehicle which in empty load.

auxiliary chamber; air suspension; neural-fuzzy control; improved genetic algorithm; ride comfort

2016-06-28 基金项目：国家自然科学基金资助项目(51575241)

江洪(1963—),女,教授,主要从事汽车工程、CAD/CAE 等方面研究，E-mail:la55@163.com。

江洪,王子豪，孔亮.半主动空气悬架的神经模糊控制[J].重庆理工大学学报(自然科学)，2017(3):1-11.

format：JIANG Hong，WANG Zi-hao，KONG Liang.Neural-Fuzzy Control Applied in Adjustable Volume Air Suspension with Additional Air Chambers[J].Journal of Chongqing University of Technology(Natural Science)，2017(3):1-11.

10.3969/j.issn.1674-8425(z).2017.03.001

U463.33

A

1674-8425(2017)03-0001-11