一维水道中潮流能可提取率的理论推导

李丹，姚炎明，2

（1.浙江大学 海洋学院，浙江 杭州 310058；2.浙江大学 舟山海洋研究中心，浙江 舟山 310600）

一维水道中潮流能可提取率的理论推导

李丹1，姚炎明1，2

（1.浙江大学 海洋学院，浙江 杭州 310058；2.浙江大学 舟山海洋研究中心，浙江 舟山 310600）

针对一维两端开放的潮流通道模型，在动力学基础上，运用流体的动量定理、质量守恒规律和能量守恒原理，推导得到通道内潮流能可提取量的计算公式以及最大可提取率的数学表达式。从推导结果可以看出，理论最大可提取率与水道海底摩阻系数、水深、水道长度、宽度等因素密切相关。此外，选取杭州湾海域建立数值模型进行实例计算，利用推导的理论公式求出不同水道的最大可提取率，最终求得海域内主要水道潮流能可提取量。

潮流能；理论最大可提取率；地形因素；动力学

海水在天体引潮力的作用下产生周期性的运动（Rourke et al，2010），其在水平方向上的流动我们称之为潮流，潮流能因其清洁高效可再生等特点获得国内外高度重视。潮流能蕴藏量虽丰富，但实际可开发量只占断面总能量的一部分，因而对开发海域的潮流能资源储量进行评估，并能够准确的计算出可开发量，对潮流能选址和开发至关重要。

目前国际上潮流能估算方法大致可以分为两种（吕新刚等，2008）：一种是基于动能通量的方法，包括Farm方法和Flux（Bryden et al，2006）方法；另一种是基于动力学方程导出的方法，包括Garrett方法 （Cummins et al，2004； Garrett， 2005）以及Vennell最新的研究方法（Vennell，2012）。国内，郑志南（1987）根据最大流速及小大潮幅值比，结合水轮机功率利用系数与机组效率推导出潮流能计算公式。

在以上方法中，以Farm方法和Flux方法应用最广。“Farm”顾名思义，可以视为涡轮机阵列或者发电装置群，可开发的资源总量等于各台设备开发量的总和。所以Farm方法估算出的潮流能资源量与开发装置的种类、效率、安装方式等直接相关，潮流能的可开发量通过乘以一系列诸如转子效率、齿轮传动效率、发电机效率等系数而得。但随着科技的发展涡轮机效率不断提高以及间隔布置的不断改进，该方法在不同时期对同一海域算得的结果相差甚大，这将导致用该方法算得结果对潮流能发电站选址的指导意义的不确定性。Black&Veatch（Bryden et al，2004；Bryden et al，2007a）提出的Flux方法在评估潮流能可开发量时，只需考虑潮流经过水道的流速、水道截面面积和有效影响因子SIF（Significant Impact Factor） （Bryden et al，2007b），即可开发功率=SIF×水道断面能通量。Flux方法也因其简单明了得到广泛的使用，但关于SIF的具体取值并没有比较精确的参考，更多的是基于实验和经验取值，计算所得的潮流能可开发量在数学层面上并不严格。

为解决这一问题，本文根据动力学原理，结合流体的动量定理、质量守恒规律和能量守恒原理，推导得到通道内潮流能可提取量的计算公式以及最大可提取率的数学表达式，并应用于实例计算。

1 公式推导

1.1动量方程

本文考虑简单一维渠道（图1），水体因为水头差Δh的存在，由水位较高一侧流向较低一侧，势能转换成动能。断面平均流速为U，断面面积A =h×b，可得出单位时间Δt内水体动量

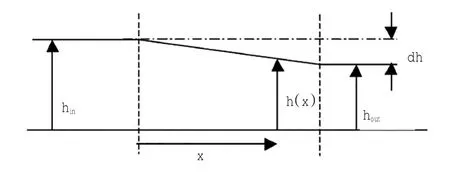
图1 简单一维渠道示意图

则作用在水体上的力即为：

随着高程的变化，水体所受单位面积上的静水压力为：

水体在流经渠道时会受到水体和地球固体交界面间产生的自然摩擦力：

式中，χ代表湿周，在一维渠道可记做χ=2h+b，τ0是水体与固边界之间的切应力，可以用谢才系数C来表示。曼宁（Manning，1890）公式

其中，R为水力半径，n为粗糙系数，简称糙率（Chin et al，2000）。

水流边界切应力用谢才系数C表示为：

潮流能发电的原理是潮流推动潮流能转换装置做功（MacLeod et al，2002），动能转换为电能。海水通过转换装置后，流速会减小，所以在理论推导的过程中，可将其视为一种摩擦力，而潮流发电装置的能量转换可理解为渠道内水体和固边界摩擦力的一种增量，记τd为涡轮机运行中水体与之的切应力τe=τ0+τd，则有效切应力，摩擦力Fd= -UΔt χτe。

综上，（2）式即：

假定水道内流态恒定，则：

1.2质量守恒

考虑到渠道的长度远小于潮波波长，本文假定∂Q/∂x=0，其中Q=U×A为单位时间水体流量。则动量方程可写成：

进一步可写成：

简化模型，即渠道宽度一定，从上式可看出，Froude系数远小于截面面积，所以：

1.3流速与水头损失之间的关系

由式（11）可得水头损失为：

在自然状态下，设渠道纵向特征流速为，摩擦力为水体和地球固体交界面间产生的自然摩擦力，根据式（5）、（6）、（12）可知：

2 理论最大可提取率的确定

当水道内不布置发电机组时，流经渠道的水流功率为：

假定在水道内布置涡轮机组如图2所示，单位时间流量为，其中，则通过涡轮机的水体势能：

Ep=ρgQ·Δh=ρgAUe·Δh （15）

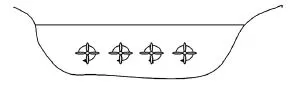
图2 水道内涡轮机分布

水体流经涡轮机的动能：

根据能量守恒原理，潮流能资源耗散量为：

对于特定的水道，可假定A、沿程水头损失Δh均一定，所以资源耗散量Pt是关于Ue的函数，因而存在一个最佳流速Uem，使得潮流能可提取量达最大，这之间的关系可由式（18）确定：

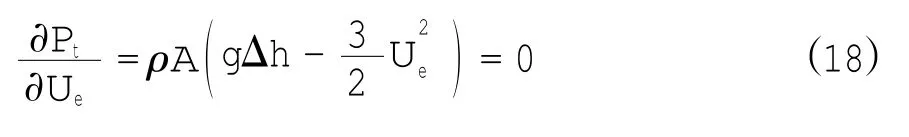
最大资源耗散量为：

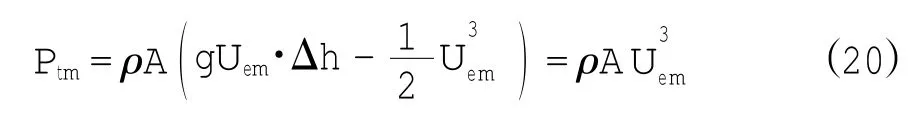
假定理论可提取量即为资源耗散量，由式（14）和式（20）可求得理论最大可提取率为：

根据这个结果可以看出，影响K取值的因素包括渠道宽度b、水深h及海底摩阻系数n、通道长度L，即水道的阻力与地形因素。当其他因素不变时，K随着长度的增大而增大；自然条件下海底摩阻系数一般取值在0.02～0.035之间，但其对K的影响较为明显；通过水道的宽度和水深能求得水力半径，即R=bh/（b+2h），由于h＜b，所以水力半径接近于水深，随着水深的变化，K的值将明显改变。这些信息为潮流能发电站的选址提供初步参考价值，即应该选择近海的潮流通道横截面积小的海岬或狭长型水道。而理论最大可提取潮能Ptm则与最大可提取系数K和流经渠道的水流总功率P0相关。

3 计算实例

3.1计算区域

图3 计算区域和曲线网格

杭州湾是一个喇叭形海湾，有钱塘江注入，湾内水域潮强流急，也是中国沿海潮差最大的海湾，潮流能资源丰富，其中尤以舟山海域各水道为甚。因而选取杭州湾区域为例，结合本文推导的理论公式，对湾口4个主要潮流通道的潮流能可开发量进行评估。本文采用国际先进的非结构有限体积数值模型（FVCOM）对整个长江口-杭州湾海域进行潮流场模拟（Chen et al，2006）。图3为计算区域和曲线网格，共10 222个网格。北支上游的分辨率大约为200 m，长江口附近为2～3 km，南边界和东边界附近为5～6 km。垂向方向采用δ坐标系，分为6层，垂向分辨率在长江口附近大约是1 m，东南水深最深处大约为8 m。模式时间步长取为180 s。

3.2模型验证

采用2009年6月20日至7月10日的潮流、潮位同步实测资料对模型进行水动力验证，各验证点分布如图4所示。图5所示为潮位验证结果，从图中可看出实测潮位与模拟计算的潮位之间拟合良好，最高和最低潮位的误差控制在10 cm以内。

图4 各验证点分布

图6 -7是潮流验证结果，从各测站潮流过程曲线可看出，相位计算结果相对误差可以控制在10%以内，流向与实测结果基本吻合；潮流流速最大值和转流时刻没有较大偏差，误差在15%以内，与实测资料吻合良好。因此，可以认为模拟计算所得的流场基本能反映模型计算区域的水动力情况。

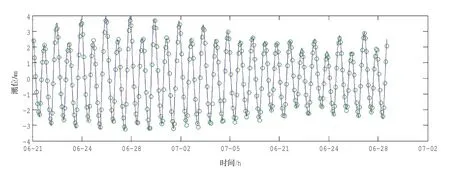
图5 乍浦潮位站潮位模拟与实测比较

图6 各测站大潮潮流流速流向验证

图7 各测站小潮潮流流速流向验证

3.3结果分析

基于数模得到计算区域的流场结果如图8所示，结合流场分布情况计算杭州湾口4个主要潮流通道的潮流能最大可开发量（表1）。关于最大可提取率K的取值，以舟山-岱山水流通道为例，舟山区域的海底摩擦曼宁系数为0.024，平均水道长度为8 m，宽度2.5 m，平均水深为40 m，所以算得K=0.219 9。

图8 模拟区域涨落潮流场分布

表1 杭州湾各主要通道潮流能可开发量

4 结论

本文通过运用流体的动量定理、质量守恒规律和能量守恒原理，推导出潮流能评估方法中理论最大可提取率的具体计算公式，与以往的经验取值相比增强了数学层面的严谨，弥补了目前基于能通量计算潮流能方法的不足。从结果可以看出，潮流通道内理论最大可提取率K与通道长度L、海底摩阻系数n、渠道宽度b及水深h等因素相关，通过这些进而可确定特定水道的潮流能最大可提取量。

需要指出的是本文针对的是一维两端开放的潮流通道模型，推导中进行了简化，实际海域地形多样，还需更加精确细致的研究。而且本文推导出的计算公式得出的是理论最大可提取率，在具体选址工作中，除考虑地形因素外，还应考虑技术层面与经济层面的因素。

Bryden I G,Couch S J,2006.ME1—marine energy extraction:Tidal resource analysis.Renewable Energy,31(2):133-139.

Bryden I G,Couch S J,2007a.How much energy can be extracted from moving water with a free surface:A question of importance in the field of tidal current energy?Renewable Energy,32(11):1961-1966.

Bryden I G,Couch S J,Owen A,et al,2007b.Tidal current resource assessment.Proceedings of the Institution of Mechanical Engineers, Part A:Journal of Power and Energy,221(2):125-135.

Bryden I G,Grinsted T,Melville G T,2004.Assessing the potential of a simple tidal channel to deliver useful energy.Applied Ocean Research,26(5):198-204.

Chen C,Cowles G,Beardsley R C,2006.An unstructured grid,finite-volume coastal ocean model:FVCOM user manual.SMAST/UMASSD.

Cummins P,Garrett C,2004.Generating power from tidal currents.Journal of Waterway,Port,Coastal,and Ocean Engineering,130(3):114-118.

Garrett C,Cummins P,2005.The power potential of tidal currents in channels.Proceedings:Mathematical,Physical and Engineering Sciences,461(2060):2563-2572.

MacLeod A J,Barnes S,Rados K G,et al,2002.Wake effects in tidal current turbine farms.In International conference on marine renewable energy-conference proceedings,49-53.

Manning R,Griffith J P,Pigot T F,et al,1890.On the flow of water in open channels and pipes.

Rourke F O,Boyle F,Reynolds A,2010.Tidal energy update 2009.Applied Energy,87(2):398-409.

Vennell R,2012.Realizing the potential of tidal currentsand the efficiency of turbine farms in a channel.Renewable Energy,47:95-102.

吕新刚，2008.海洋潮流能资源估算方法研究进展.海洋科学进展，26（1）：98-108.

郑志南，1987.海洋潮流能的估算.海洋通报，（4）：70-75.

（本文编辑:袁泽轶）

Theoretical derivation of the extractable rate of tidal current energy in one-dimensional flow channel

LI Dan1,YAO Yan-ming1，2

（1.Ocean College， Zhejiang University,Hangzhou 310058,China;2.Zhoushan Ocean Research Center, Zhejiang University,Zhoushan 316000,China）

A theoretical formula for estimating the extractable power of tidal currents in tidal channels is derived with a formation of maximum extractable coefficient presented.This derivation is based on the conservation of mass,conservation of momentum and conservation of energy in one dimensional inlet and outlet tidal channel model.The theoretical result shows that the maximum extractable coefficient is related with the fraction of channel bottom,the depth of the channel,the length of the channel and the width of the channel.This formula is further applied to estimate the power potential in the Hangzhou Bay based on the numerical results of the Hangzhou Bay.

tidal current energy;optimal extractable rate;terrain factors;dynamics

P731.2

A

1001-6932（2017）01-0037-06

10.11840/j.issn.1001-6392.2017.01.005

2015-09-19；

2015-12-22

李丹（1991-），女，硕士研究生。电子邮箱：21334036@zju.edu.cn。

姚炎明，副教授。电子邮箱：hotfireyao@163.com