拨云见日——回归直线方程计算释疑

湖北省松滋市第二中学(434200) 卢涛

拨云见日
——回归直线方程计算释疑

湖北省松滋市第二中学(434200) 卢涛

回归直线方程的计算能力包括根据法则公式进行准确计算,变形和数据处理,也指能根据问题的条件寻找与设计合理而简捷的运算途径.

回归直线方程计算是高考中的热点题型,课本上对回归直线方程系数公式推导过程复杂,很多学生最终形成只会套公式,不会对数据灵活处理,导致学生盲目套用公式,计算困难.下面从回归直线方程系数的推导过程,回归直线方程的原理理解,数据处理技巧,公式变形应用这四个方面加以说明以供大家参考.

一、回归直线方程系数推导之疑

课本上推导原理简单但推导过程复杂,学生不易掌握.在此,通过导数求极值优化推导过程,便于学生理解.

评注通过将a与b分别看成变量,通过求导求函数的极值的方法求Q(a,b)最小值,学生容易掌握推导出回归直线方程系数公式,以便加深理解回归直线方程原理.

二、回归直线方程原理理解之疑

例题(2011年高考广东卷理科13)某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm、和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为___cm.

疑问学生弄不清解释变量与预报变量,误将x视为1,2,3计算出错,需要注意儿子身高与父亲身高有关,将父亲身高作为解释变量,儿子身高做为预报变量.依次列出对应点的坐标.

评注计算回归直线方程时首先找准解释变量和预报变量,然后列出对应的解释变量和预报变量的坐标,为计算方程做准备.在的计算上面,很明显选择前一种形式公式计算简便.

三、数据计算之疑

例题(2011安徽卷)某地最近十年粮食需求量逐年上升,下表是部分统计数据：

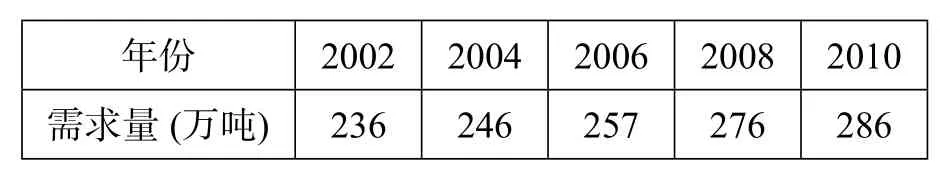
年份2002 2004 2006 2008 2010需求量(万吨) 236 246 257 276 286

(II)利用(I)中所求的直线方程预测该地2012年的粮食需求量.

评注为了方便计算先将x同时减去一个数,将大数化小,有时最好减去x的平均值(根据公式特点),再将y也同时减去一个数,这个处理过程相当将所有数据进行了左右,上下平移变换,将数据化小使得数据方便计算.

解析(1)由所给数据看出,年需求量与年份之间是近似直线上升.下面来配回归直线方程,为此对数据预处理如下：

由“年份”-2006得：-4,-2,0,2,4;由“需求量”-257得：-21,-11,0,19,29对预处理后的数据,容易算得¯x=0,

(2)利用直线方程①,可预测 2012年的粮食需求量为：(万吨)≈300(万吨).

四、公式变形之疑问

例题(2016高考新课标III文数)下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图

图1

(I)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;

(II)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.

评注高考不仅考察基本计算,而且考察对数据的处理变形,因此适当变形处理数据很有训练必要.

回归直线方程的计算只要我们理解原理,熟悉回归直线方程系数的推导过程,掌握公式之间的转换,会进行简单的数据处理技巧,认真细致运算,相信大家这题一定会手到擒拿!

[1]史雄,关于回归直线方程的另一种简单计算〔J〕,新课程学习(基础教育)2010,(02).