基于参数漂移的机载设备检测间隔优化
2017-04-05黄加阳左洪福闫洪胜
黄加阳,左洪福,蔡 景,闫洪胜
(1.北京航空航天大学,北京 100191; 2.上海民用飞机健康监控工程技术研究中心,上海 200241;3.南京航空航天大学,南京 211106)
【后勤保障与装备管理】
基于参数漂移的机载设备检测间隔优化
黄加阳1,2,左洪福3,蔡 景3,闫洪胜3
(1.北京航空航天大学,北京 100191; 2.上海民用飞机健康监控工程技术研究中心,上海 200241;3.南京航空航天大学,南京 211106)
为提高具有参数漂移特征设备的可靠度,开展了基于参数漂移的检测间隔优化研究。针对设备参数存在随机干扰的现象,采用异常值检验法,研究了干扰参数的剔除方法;以剔除异常值后的参数为基础,采用无偏估计方法,对设备参数的漂移系数和扩展系数进行了估计研究;建立了可靠度与参数漂移量之间的定量关系,根据设备的可靠度的要求,优化得到检测间隔值,通过实例进行了验证。
参数漂移;检测;间隔;优化
大量的电子设备在实际工程应用中由于自身性能退化或者受到使用环境,譬如电流、电压、湿度、温度和振动等的影响,会存在参数漂移的现象[1-2]。如参数的漂移被限定在一定的范围内,通常不会造成设备的故障;但是,随着设备使用时间的增加,或者使用环境的恶化,参数漂移的偏离速度和波动幅度逐渐提高。当参数漂移超过规定的范围时,就会导致可靠度降低,甚至设备失效。
为了避免设备失效事件的发生,需要定期检测设备的参数。如果检测间隔过长,那么很多设备在检测之前就已经发生参数严重漂移导致大量失效事件发生;如果检测间隔过短,会导致过多的干预设备运行并且使得相应的人力和成本增加。因此,有必要根据设备已有的检测数据,优化得到一个合理的设备检测间隔[3]。
在已有的设备检测数据中,有些数据属于异常数据,是由于突发因素或者偶发因素造成的,譬如外界某个强电场或强磁场的随机干扰,这种干扰会引起参数的大幅度漂移,但持续时间较短,而且随着干扰的消失,参数波动会回到原有的水平。因此,随机干扰通常不会造成设备的功能故障。但是这些受随机因素干扰的参数值需从已有数据中剔除,以免对设备整体参数的漂移研究以及检测间隔优化造成影响。
为此,本文首先采用异常值检验法,剔除受随机因素干扰的参数值。在此基础上,采用无偏估计,对设备参数的漂移系数和扩展系数进行估计。最后,建立可靠度与参数漂移量的定量关系,从而优化得到特定可靠度要求下的检测间隔值,并进行实例验证。
1 参数的异常检验
在实际工程中,工程技术人员凭借经验经常会从技术或者物理层面判断一个设备的参数是否属于异常值。但是在设备量或参数记录数非常多的情况下,这种基于经验的方法,有时会变得难以执行,而基于统计的异常值剔除法相对更加有效。
异常数值检验方法有很多,比较通用的方法有:奈尔检验法、格拉布斯检验法、狄克逊检验法、偏度-峰度检验法、Fisher型统计检验法、G和D型统计检验法等。虽然方法各不相同,但找出异常值的效果基本类似。本文采用相对通用的奈尔检验法,对设备参数进行异常数值检验。奈尔检验法有上侧情形检验法、下侧情形检验法和双侧情形检验法之分[4-6]。本文采用更具代表性的双侧情形检验法进行异常检验,假定有n个按检测间隔期T,多次检测得到的设备参数的样本值,排列序列为
(1)
(2)

根据以上的步骤,可以对剔除异常值的参数序列进行进一步的异常值检验,直至没有异常值为止。
2 设备可靠度与参数漂移量的定量关系
2.1 漂移参数的估计
假定设备在0时刻,参数完全正常,处于原点x0。经过时间T进行检测, 检测得到的参数值x(T),参数漂移量记为Δx(T),即
经过大量的实践统计表明Δx(T)服从均值为C·T,方差为D·T的正态分布[7-8],即
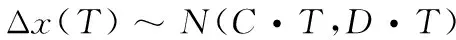
其中:C为设备参数的漂移系数;D为设备参数的扩展系数。
由于x(T)=x0+Δx(T),因此x(T)服从
(3)
假定经过异常值检验后得到的样本容量为m(m≤n),对应的样本分别为
因此,可得
(4)
因此,可得
(5)
2.2 设备可靠度与参数漂移量
假定设备允许的参考变化范围是[xL,xH];xL,xH分别为参数允许的最小值和最大值。参数从原点x0开始,经过一定时间T后,参数值x(T)依旧处于[xL,xH]范围内的概率,即为设备的可靠度R(T)。显而易见,随着检测间隔T的增加,x(T)处于[xL,xH]范围内的概率减少,因此,必须要选择合适的间隔T值,确保设备的可靠度[9]。
根据正态分布函数性质,可得

(6)
式中φ(x)为标准正态分布函数。因此,根据设备的可靠度要求Rreq值,可以反推得到设备的检测间隔T*值。
3 实例分析
已知某发动机控制系统的燃油泵额定的压力允许变化范围为(45 MPa,55 MPa)。该部件原定的检测间隔是30天,每次检测得到的数据如表1所示,检测后通过修复压力恢复到标准值x0=48 MPa。

表1 燃油泵30天的压力检测值
3.1 异常参数的剔除
根据式(1)和式(2)可以得到
表2列出了部分奈尔检验法临界值,从表2可以看出,如果取检出水平α=5%,则可得
R1-0.05/2(30)=3.089

表2 奈尔检验法临界值(部分)
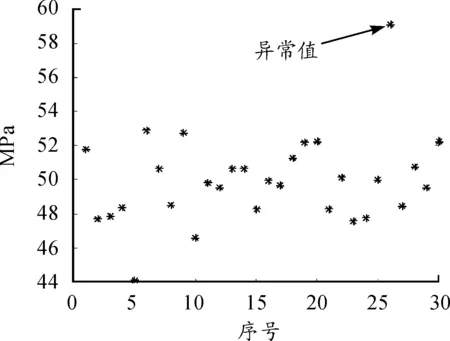
图1 检测参数序列及异常值
剔除异常值以后,重新进行奈尔检验,根据式(1)和式(2)可以得到
根据奈尔检验法的判定准则,重新判定为无异常值存在。
3.2 参数漂移参数的估计
基于表1中除去序号26的检测数据,进行参数估计,按照式(4)和式(5),分别可得

所以,根据式(3),可知x(T)服从
x(T)~N(50+0.055 2·T,0.136 4·T)
3.3 检测间隔的优化
根据发动机控制系统的燃油泵额定压力允许的变化范围可知:xL=45 MPa,xH=55 MPa。所以,根据式(6)可得
(7)
由式(7)可以得到可靠度R(T)与检测间隔T的关系如图2所示。

图2 可靠度R(T)与检测间隔T的关系
根据图2,可以得到特定可靠度条件下的检测间隔值,譬如:设备的可靠度要求为0.99或0.98,那么对应得到的检测间隔
根据以上的研究,就可以根据发动机控制系统燃油泵的不同使用可靠性要求,优化调整检测间隔。
4 结束语
针对具有参数漂移特征的设备,利用已有的设备检测参数,通过研究异常值检验法,以及基于无偏估计的参数漂移系数和扩展系数的估计方法,建立了设备可靠度与参数漂移量的定量关系,实现了对设备检测间隔值的优化,对设备的运行维护具有指导意义。
[1] 翟亚利,张志华,李大伟.具有漂移特征的退化可靠性评估方法研究[J].系统工程理论与实践,2014(10):2710-2715.
[2] 翟亚利,张志强,钟强晖.具有参数漂移特征的退化可靠性评估方法[J].海军工程大学学报,2013(2):107-112.
[3] 张晓燕.飞行间隔标准的安全评估研究[D].天津:中国民航大学,2007.
[4] 温雯,郝志峰,杨晓伟,等.基于假设检验及异常点剔除的稳健LS-SVM回归[J].模式识别与人工智能,2010(2):241-249.
[5] 邵婷婷,张水利,张永波.两种剔除异常数据的方法比较[J].现代电子技术,2008(24):148-150.
[6] 李丽容,田琛.工程测量中异常数据的剔除[J].石油仪器,1998(5):28-29.
[7] 苏再兴,王志福,万莹,等.基于正态分布参数无偏估计的几个结果[J].渤海大学学报(自然科学版),2010(3):250-254.
[8] 陈春华.缺失数据下特殊指数分布参数的无偏估计[D].武汉:华中师范大学,2008.
[9] 李彦彬,府天洁,刘成绪.一种基于定期检测的导弹可靠度计算方法[J].四川兵工学报,2011(10):1-3.
(责任编辑 唐定国)
Inspection Interval Optimization Method of Airborne Equipment with Parameters Drift Feature
HUANG Jia-yang1,2,ZUO Hong-fu3,CAI Jing3,YAN Hong-sheng3
(1.Beihang University, Beijing 100191, China; 2.Shanghai Engineering Research Center of Civil Aircraft Health Monitoring, Shanghai 200241, China; 3. Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China)
In order to improve the reliability of the equipment with parameter drift, the optimization of the inspection interval based on the parameter drift was carried out. Firstly, accordingly to the phenomenon of random interference existing in collecting equipment parameters, outlier test method was applied to eliminate the data with random interference; Secondly, based on the remaining parameters without random interference, unbiased estimation method was studied to obtain drift coefficient and expansion coefficient of parameters; Finally, the quantitative relationship between reliability and parameter drift was researched to optimize the inspection interval of equipment based on required reliability of the equipment, and the method was verified by an example.
parameters drift; inspection; interval; optimization
2016-10-12;
2016-11-15 作者简介:黄加阳(1983—),男,硕士,高级工程师,主要从事民机可靠性分析与健康管理研究。
10.11809/scbgxb2017.03.023
黄加阳,左洪福,蔡景.基于参数漂移的机载设备检测间隔优化[J].兵器装备工程学报,2017(3):101-103.
format:HUANG Jia-yang,ZUO Hong-fu,CAI Jing, et al.Inspection Interval Optimization Method of Airborne Equipment with Parameters Drift Feature[J].Journal of Ordnance Equipment Engineering,2017(3):101-103.
TB114.3
A
2096-2304(2017)03-0101-03
