基于序贯截尾检验的一维修正弹精度评估方法
2017-04-05吴艳征
马 康,吴艳征
(中国人民解放军92941部队,辽宁 葫芦岛 125001)
【装备理论与装备技术】
基于序贯截尾检验的一维修正弹精度评估方法
马 康,吴艳征
(中国人民解放军92941部队,辽宁 葫芦岛 125001)
基于序贯截尾检验方法,对一维修正弹的落点密集度的评估方法进行了研究,采用Monte-carlo法给出了数值算例,仿真计算结果表明,通过序贯截尾检验方法,能够有效减少试验次数,缩短试验周期,能够为该型信息化弹药的试验鉴定提供理论参考,具有较强的理论价值和一定的参考意义。
一维修正弹;序贯截尾检验;落点密集度
为满足现代战争的需求,精确打击、远程火力压制和远程火力支援弹药将得到大量的应用,而传统的常规炮射弹药不能达到对敌作战的预期效果,一维修正弹就是在此背景下诞生的一种成本低、精度高、射程远、能批量生产并适合现代战争需要的强力打击弹药[1-6]。
一维修正弹作为舰炮信息化弹药,其工作原理是利用舰载雷达跟踪测量弹道、火控预测弹道偏差,通过舰载雷达发送修正指令,增程修正弹接收指令、在预定时间实现距离修正、提高纵向密集度。由此可见,弹丸落点密集度是一维修正弹的重要战技指标,也是靶场鉴定试验中必须重点考核的试验项目之一。作者基于序贯截尾检验方法[7-9],对一维修正弹的落点密集度的评估方法进行研究,试图为该型信息化弹药的鉴定试验提供理论参考。
1 落点密集度的评价指标
落点密集度的特征量包括纵向密集度和横向密集度:其中纵向密集度用最大射程的纵向概率误差EX与最大射程X的比值(EX/X)来度量,横向密集度用最大射程的方向概率误差EZ来度量。
假设进行了N组一维修正弹密集度试验射击,各组均为相同的射击条件,每组射击n0发弹药,其中第i组射击试验的第j发弹的落点纵向偏差和横向偏差为(ΔXij,ΔZij),其中i=1,2,…,N,j=1,2,…,n0。这N组数据就构成了一个密集度试验数据样本。
以纵向落点密集度为例,落点纵向偏差的均值为
(1)
落点纵向偏差的方差最大似然估计如式(2)所示
(2)
纵向概率偏差为
(3)
而纵向概率误差EX与最大射程X的比值(EX/X)就是一维修正弹纵向密集度的评价指标。
2 落点密集度的序贯截尾检验评估方法
对于一维修正弹落点密集度试验样本,可以认为落点偏差(x,z)是服从正态分布的随机变量,总体的均值和方差均为未知的样本,纵向偏差x和横向偏差z相互独立,即X~N(μx,σx),Z~N(μz,σz),其中μx、μz、σx和σz均未知。
下面,以纵向密集度序贯检验为例,研究正态总体方差的序贯检验方法。
2.1 正态总体方差的序贯检验方法
1) 建立关于样本标准方差σ的互相竞择的检验假设:
(4)
式中:σ0为规定的落点纵向标准偏差指标值;σ1为使用方不希望但能接受的最大落点纵向标准偏差指标;λ为鉴别比,且λ>1。
2) 选择研制方风险α和使用方风险β,风险率α和β由双方商定,一般采用风险相当原则;
3) 计算两个常数A与B的值,可由计算式确定:
(5)
(6)
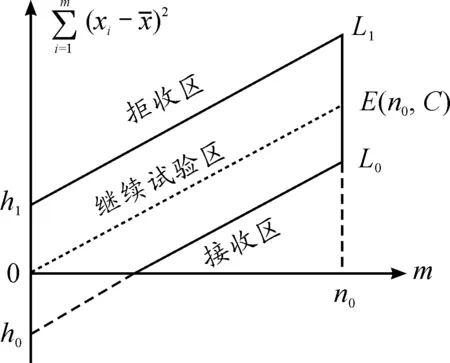
式中:A与B的值应满足0 4) 进行判别 经过m次一维修正弹密集度试验,得到落点偏差纵向子样(x1,x2,…,xm)。 当假设H0:σ=σ0为真时,出现子样(x1,x2,…,xm)的概率为 (7) 当假设H0:σ=σ1为真时,出现子样(x1,x2,…,xm)的概率为 (8) 接下来,对试验进行判别: a) 当 (9) 继续进行第(m+1)次试验; b) 当 (10) 采纳统计假设H0,试验结束; c) 当 (11) 拒绝统计假设H0,试验结束。 由于正态总体的均值μx未知,根据文献[10]可知,在式(12)~式(13)中,可用子样(x1,x2,…,xm)的均值 (15) 代替正态总体的均值μx,且公式中等号右端的m变为(m-1)即可。 即对于正态总体的均值μx未知的子样(x1,x2,…,xm),其判别法则变为: 当 (16) 继续进行第(m+1)次试验;当 (17) 采纳统计假设H0,试验结束;当 (18) 拒绝统计假设H0,试验结束。 2.2 序贯截尾检验方法 序贯截尾检验法是为了使序贯简易方法避免试验次数的不确定性并尽量减少试验次数,常常提出试验次数的上界,在此上界以内应用序贯检验法。如果能在上界以内做出决策,则试验结束,节省试验次数,但当试验次数达到上界时,必须做出决策,不允许再继续试验。 对于式(4)给出的假设检验,在给定的双方风险α和β条件下,当进行完n0次试验后,可应用式(16)~式(18)进行判别。如果仍落在继续试验区,而序贯检验又必须在n0处截尾,可按下列截尾方案进行判定: 1) 当满足式(19)时,采纳假设H0 (19) 2) 当满足式(20)时,拒绝假设H0 (20) 式中: (21) 图1 序贯截尾检验图 2.3 序贯检验截尾数的确定方法 截尾数n0与试验次数n的期望值E(n)有关,在截尾数n0的实际计算中,往往采用Monte-carlo法进行模拟计算。其基本流程为: 1) 产生N(0,1)的随机数yi,记xi=μ+σyi,则xi为服从N(μ,σ)分布的随机数; 2) 利用步骤1)进行模拟抽样试验,得到一个观察值,如果该观察值落在继续试验区,则进行下一次随机抽样,连同前面抽样结果计算一个新观察值,然后再判断是否进行下一次随机抽样,直到新的观察值落在拒收区域或接收区域,该次试验终止,把从抽样开始到序贯抽样终止称为一次模拟试验,抽样次数为mi; 3) 按上述模拟方法试验进行N次,N是一个很大的正整数,本算例中取N=20 000,得到各次模拟试验的抽样次数:m1,m2,…,mN; 4) 计算得到抽样次数的期望值,即序贯试验平均试验次数为 (22) 5) 计算试验实际风险率α′和β′; 6) 截尾数n0=E(m)。 假定一维修正弹落点纵向标准偏差指标值为σ0=100,由式(4)建立互相竞择的检验假设: (23) 需要注意的是,在实际一维修正弹试验方案中,一般设置一组固定射击m发,每射击一组之后再进行一次假设检验,即每完成一组射击之后,才生成一个观察值,然后按照式(16)~式(18)判断该观察值落在继续试验区,还是落在拒收区域或接收区域,而不是射击一发就进行一次假设检验。本算例中取m=4,即n0次试验共射击4n0发一维修正弹。应用Monte-carlo统计模拟试验法,计算不同λ、α和β条件下,双方实际风险α′和β′和平均试验次数n0,即给出一维修正弹纵向密集度序贯检验方案。如表1所示。 表1 序贯截尾检验方案表(每组射击m=4发) 从表1中给出的9种试验方案中,选择一种合理、可行的试验检验方案。 推荐方案一:取鉴别比λ=1.2,双方风险α=β=0.25,截尾数n0=8,即射击8组,共击发32发弹药,而实际弃真概率(研制方实际风险)α′=0.168 5,实际采伪概率(使用方实际风险)β′=0.230 9。 推荐方案二:取鉴别比λ=1.3,双方风险α=β=0.2,截尾数n0=6,即射击6组,共击发24发弹药,而实际弃真概率(研制方实际风险)α′=0.107 6,实际采伪概率(使用方实际风险)β′=0.169 4。 落点密集度已成为衡量一维修正弹能否完成使命任务的关键指标,也是靶场必须考核和评估的试验项目。本文基于序贯截尾检验方法,对一维修正弹的落点密集度的评估方法进行研究,为该型信息化弹药的鉴定试验提供理论参考。采用Monte-carlo法进行了数值计算,仿真计算结果表明,通过序贯检验方法,能够有效减少试验次数,节省用弹量,具有一定的理论参考和工程应用价值。 [1] 陈维波,纪永祥,陈战旗.基于扩展卡尔曼滤波的射程修正落点预测模型[J].探测与控制学报,2013,35(3):8-11. [2] 黄义,汪德虎,余家祥,等.舰炮一维弹道修正弹射击误差分离和校正研究[J].指挥控制与仿真,2012,34(3):44-46. [3] 黄义,汪德虎,汪汇川,等.舰炮发射一维修正弹多发同时弹着研究[J].弹箭与制导学报,2012,32(5):127-129. [4] 刘奎永,黄守训,郝瑞云.序贯分析法在舰炮武器试验中的应用[J].火力与指挥控制,2004,29(1):98-102. [5] 舒长胜,孟庆德.舰炮武器系统应用工程基础[M].北京:国防工业出版社,2014. [6] 黄士亮,田福庆,张威,等.舰炮试验与鉴定[M].北京:国防工业出版社,2011. [7] 郑锦,丛树学,武翰文.一种新的火炮武器系统射击精度试验方法[J].指挥控制与仿真,2008,30(1):98-102. [8] 孙晓峰,赵喜春.导弹试验中序贯检验及序贯截尾检验方案的优化设计[J].战术导弹技术,2001(1):9-16. [9] 于录,曲宝忠,时维科.反舰导弹单发命中概率检验方法[J].海军航空工程学院学报,2012,27(1):23-26. [10]张金槐,李菊生.飞行器试验统计学(上册)[M].长沙:国防科技大学出版社,1982. [11]舒延春.一维修正弹射击校正方法[J].四川兵工学报,2015(2):1-3. (责任编辑 周江川) Evaluation Method on Dispersion of Impact Point for One Dimension Trajectory Correction Projectile Based on Sequential Truncated Inspection MA Kang, WU Yan-zheng (The No. 92941stTroop of PLA, Huludao 125001, China) On the basis of the sequential truncated inspection method, the evaluation methods on the dispersion of impact point of the projectile have been analyzed. The numerical examples have also been given by applying the Monte-carlo method, and the results show that test times and test cycle can be reduced by applying the sequential truncated inspection, The researches can provide theoretical references for the test and evaluation of the projectile and show its military and economic effects. one dimension trajectory correction projectile; sequential truncated inspection; dispersion of impact point 2016-10-09; 2016-11-20 作者简介:马康(1981—),男,博士,工程师,主要从事舰炮武器系统试验研究。 10.11809/scbgxb2017.03.007 马康,吴艳征.基于序贯截尾检验的一维修正弹精度评估方法[J].兵器装备工程学报,2017(3):31-34. format:MA Kang, WU Yan-zheng.Evaluation Method on Dispersion of Impact Point for One Dimension Trajectory Correction Projectile Based on Sequential Truncated Inspection[J].Journal of Ordnance Equipment Engineering,2017(3):31-34. E919 A 2096-2304(2017)03-0031-04
3 应用实例
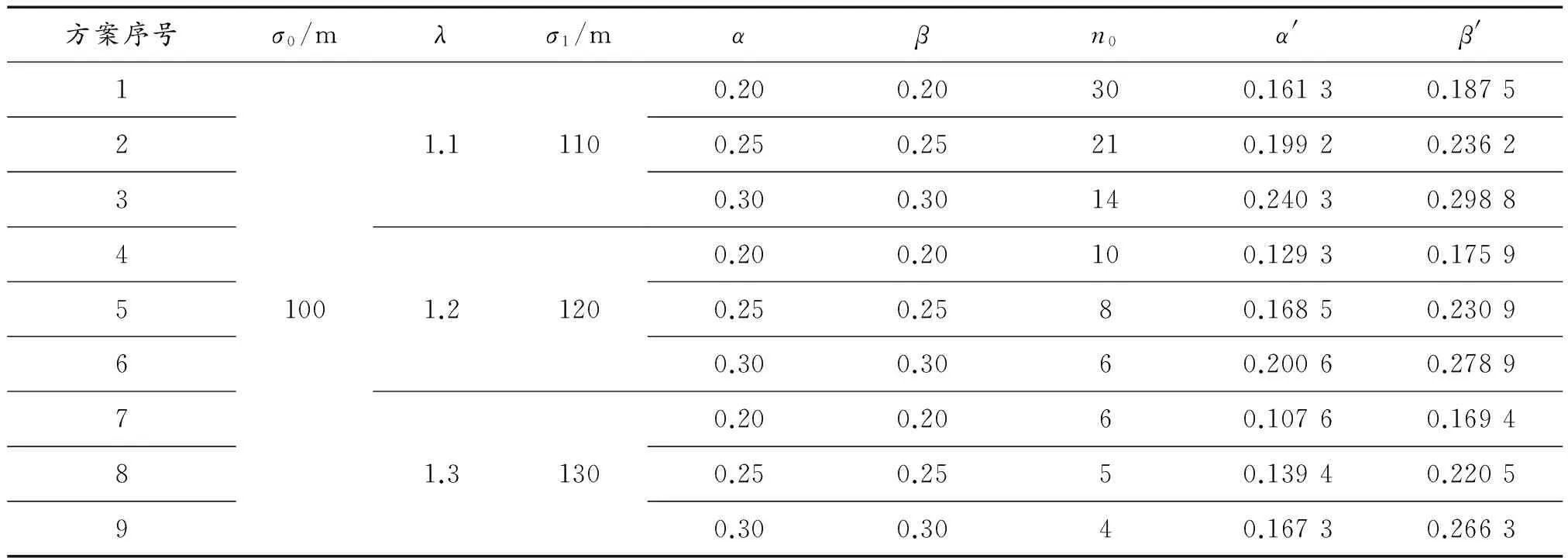
4 结束语
