计及热传导影响对长杆弹侵彻陶瓷靶的数值分析*

李芮宇,孙宇新,周 玲,孙其然,赵亚运,冯江拓

(1.南京理工大学瞬态物理重点实验室,江苏南京210094; 2.中国兵器科学研究院,北京100000)

计及热传导影响对长杆弹侵彻陶瓷靶的数值分析*

李芮宇1,孙宇新1,周 玲2,孙其然1,赵亚运1,冯江拓1

(1.南京理工大学瞬态物理重点实验室,江苏南京210094; 2.中国兵器科学研究院,北京100000)

采用有限元方法离散瞬态热传导方程,编写成侵彻过程热传导计算模块,并将之嵌入已有的冲击动力学程序中,然后运用于长杆弹在900～1 800 m/s着速范围内侵彻AD95陶瓷靶的数值分析,得到了符合物理事实的计算图像,所得的计算结果比采用传统的绝热模型得到的计算结果更符合实验结果。探讨了计及热传导效应对长杆弹侵彻AD95陶瓷靶数值模拟的影响:着速在900～1 350 m/s范围内时,计及热传导的数值计算所得侵深小于绝热模型计算结果;着速在在1 350～1 450 m/s范围内时,两种模型计算侵深接近;着速在在1 450～1 800 m/s范围内时,热传导模型计算侵深大于绝热模型计算结果。

侵彻;热传导;有限元;陶瓷

长杆弹侵彻过程中,弹靶界面塑性变形严重,产生大量的热,引起材料温升,进而导致材料的力学性能发生改变。所以,侵彻计算时必须考虑温度因素。对此,李永池等[1]对钨合金热塑性互动损伤和平头弹丸冲塞进行了计算,考虑了温度对材料参数和损伤演化的影响;晏麓晖等[2]研究了绝热软化对空腔膨胀数值模拟的影响,发现不计入热效应会高估侵彻阻力;赵攀峰等[3]将温度软化考虑进数值计算中,研究了杆弹高速贯穿金属靶的有关规律。材料出现局部温升必然存在热传导现象,影响材料的温度分布和力学行为。然而,既往的数值计算[4-6]中普遍忽略了热传导因素,计算结果必然与真实状况存在差异。

本文中,将热传导模块嵌入冲击动力学源代码,运用于长杆弹侵彻AD95陶瓷靶的数值分析,并将得到的计算结果与绝热模型计算结果进行比较。

1 计算物理模型

IMPACT-2D是基于连续介质力学的Lagrange型基本守恒方程所编写的源代码,主要用于高速撞击现象的数值分析和数值模拟计算,是在借鉴其他有限元软件的基础上开发完成的。但是在软件开发初期未考虑冲击过程中的热传导,无法分析热传导对冲击问题模拟的影响,所以有必要引入热传导方程。轴对称导热微分方程为:

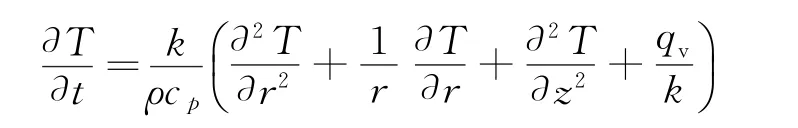
式中:T为物体的瞬态温度,t为时间,k为材料的导热系数,ρ为材料密度,cp为材料的比热,qv为材料的内热源强度。

由于有限元热传导计算是基于节点的,而有限元冲击计算的温度储存在单元中,程序在计算单元应力时采用的也是单元的温度,只是在后处理时将单元的温度转换在节点上。但是无法通过该转换方法将节点的温度再转换回单元,所以在进行热传导计算时必须建立一个背景网格,方法是:以单元的中心节点为热传导计算的节点,以此构建背景网格。每一个循环结束后,以单元的温度为初始条件作为背景网格节点的温度,进入热传导模块进行计算,这样就实现了单元温度的更新,并以更新后的单元温度进行下一步循环计算。如此一来,程序就实现了冲击过程中的热传导计算。图1为背景网格示意图:i～l为原始三角形单元,1～6为原始三角形单元节点,用于计算侵彻过程中材料的应力应变等;a～d为背景网格节点,用于原始单元之间的热传导计算。

2 模型及参数

针对孙宇新等[7]的长杆弹侵彻陶瓷复合靶的实验进行数值模拟,弹丸材料为35Cr MnSi,口径为7.62 mm,长约70 mm。复合靶由盖板/陶瓷靶/鉴证靶组成,靶板直径为96 mm。盖板的材质为A3钢,厚度为2 mm;陶瓷靶材质为AD95陶瓷,直径为80 mm,总厚度为30 mm;鉴证靶材质也采用A3钢。在陶瓷靶外紧围一圈由45钢制成的套筒以实现对陶瓷的径向约束,壁厚8 mm。建立二维轴对称离散模型,如图2所示,三角形单元总数为36 000。

采用线性温升软化关系[8]计算温度对弹性模量、泊松比等物理量的影响,采用Johnson-Cook本构模型描述温度对金属材料屈服应力的影响,并采用Grüneisen状态方程。35Cr MnSi[9]、A3钢[10]和45钢[11]的材料参数如表1所示。对AD95陶瓷材料采用JH-2模型[12]描述,参数[13]分别为:ρ0= 3.625 g/cm3,A=0.88,N=0.64,C=0.007,σt=0.262 GPa,B=0.28,M=0.60,σHEL=5.3 GPa,σHEL,eff=3.75 GPa,pHEL=2.8 GPa,G=109.7 GPa,K1=228.6 GPa,K2=191.4 GPa,K3=111.5 GPa,

图1 温度背景网格示意图Fig.1 Diagram of temperature background grid

图2 模型及局部网格Fig.2 Model and local mesh

表1 3种金属的材料参数Table 1 Parameters of three metals

3 计算结果及分析

3.1 结果验证

图3给出了考虑热传导时,着速为1 054 m/s的长杆弹对陶瓷复合靶的侵彻过程。弹体的销蚀、盖板的鼓起、陶瓷靶正面的开坑、陶瓷靶内部裂纹的扩展等现象在图3中均得到了清晰的描述,与图4实验现象十分吻合,这也表明本文中所用程序及选取的材料模型及参数是可靠的。

图3 典型长杆弹侵彻陶瓷靶过程中的损伤云图(1 054 m/s)Fig.3 Damage distribution of the ceramic target penetrated by a typical long-rod projectile of 1 054 m/s

图4 典型长杆弹侵彻后的AD95陶瓷靶(1 054 m/s)Fig.4 AD95 ceramic target penetrated by a typical long-rod projectile of 1 054 m/s

3.2 模拟结果分析

3.2.1 侵深与着速的关系

图5给出了分别采用绝热模型和热传导模型计算得到的长杆弹侵深D随着速v0的变化关系(图5 (a))以及两种模型计算侵深的差值百分比随弹体着速的变化关系(图5(b)),其中D1为热传导模型计算侵深,D2为绝热模型计算侵深。由图5(b)可以看出两种模型计算侵深的差值百分比最大可达3%,因此热传导因素对长杆弹侵深有较显著的影响,当弹体着速在900～1 350、1 350～1 450和1 450～1 800 m/s等3个范围内时,热传导模型计算侵深分别小于、接近、大于绝热模型计算结果。由图5(a)可以看出热传导模型计算结果同实验结果最接近,这说明在侵彻计算中对弹体考虑热传导效应很有必要。下面将从侵彻过程中长杆弹的面密度变化、压力变化等方面来解释图5呈现的现象。

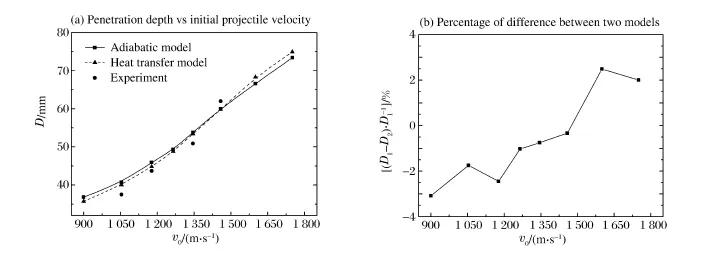
图5 两种模型计算侵深的比较Fig.5 Comparison between the two models on penetration depth

3.2.2 弹体侵彻过程中的面密度和侵深

在此取2个典型着速(900和1 750 m/s)来说明问题,这2个着速分别代表图5中的2种情况:热传导模型计算侵深低于和高于绝热模型计算侵深。图6(a)、(b)分别为900和1 750 m/s着速下的弹体面密度ρa和侵深时程曲线。由图6可以发现对应的2种侵彻过程:(1)弹体着速为900 m/s时,在约40μs后热传导模型对应的弹体面密度开始显著小于绝热模型对应的弹体面密度,以致其侵彻过程所承受的平均过载较大,最终使得侵深低于后者;(2)弹体着速为1 750 m/s时,总体上,热传导模型对应的弹体面密度高于绝热模型对应的弹体面密度,其平均过载也就低于后者,侵深比绝热模型计算结果大。

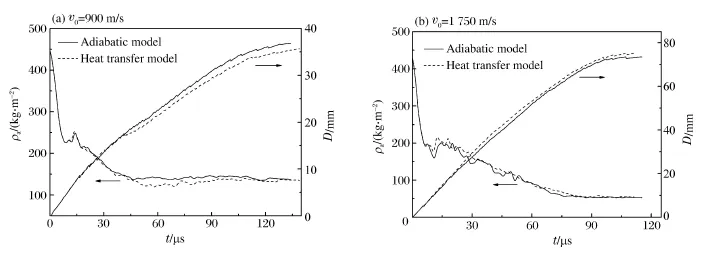
图6 弹体面密度和侵深时程曲线Fig.6 Areal density-and penetration depth-time curves of the long-rod projectile at different initial penetration velocities

3.2.3 侵彻过程中的弹头压力变化

图7给出了2种典型着速下侵彻过程中弹头的压力时程曲线,在900和1 750 m/s的着速下,弹体侵彻过程所受的最大压力分别为10和22 GPa,远高于弹体材料的静态屈服强度Y0(1.64 GPa)。图8为侵彻过程中弹头平均压力p随弹体着速的变化关系,可见随弹体着速v0的升高,弹头在侵彻过程中所受平均压力也随之升高,可将本文中长杆弹侵彻陶瓷复合靶的过程分为3个阶段,见表2。

图7 侵彻过程中弹头的压力时程曲线Fig.7 Pressure-time curves of the projectile head during penetration

图8 侵彻过程中弹头平均压力随着速的变化Fig.8 Average pressure of the projectile head varied with initial penetraion velocity during penetration

表2 长杆弹侵彻陶瓷复合靶3个阶段Table 2 Three phases of long-rod projectiles penetration into ceramic composite targets

3.2.4 原因分析

由3.2.1～3.2.3节的分析可知,热传导对长杆弹侵彻计算有较显著的影响,且存在如图5和表2所示的规律。图9为900和1 750 m/s的着速下长杆弹侵彻过程中的剩余质量变化,可见在着速为900 m/s时热传导模型对应的剩余质量一直小于绝热模型对应的剩余质量;着速1 750 m/s时,热传导模型对应的剩余质量一直大于绝热模型对应的剩余质量,90μs后热传导模型对应的剩余质量开始向后者靠拢。由以上可以认为:当着速较低时(小于1 350 m/s),考虑热传导因素会使弹体在侵彻过程中销蚀更快;当着速较高时(大于1 450 m/s),考虑热传导因素会使弹体在侵彻过程中销蚀变慢。

图9 两种模型长杆弹剩余质量时程曲线Fig.9 Residual mass-time curves by two models

图10 观测点温度时程Fig.10 Temperature-time curves of observation points

有限元计算中,单元的销蚀与塑性应变相关,塑性应变达到阈值时,会被删除。考虑热效应时,单元的应变与温度有很大的关系,单元温度升高,材料的剪切模量和屈服应力会下降,单元抵抗变形的能力也随之降低,其应变就会越早达到阈值,被删除。图10给出了弹体轴线距弹头20 mm处单元的温度时程曲线,可见:900 m/s时热传导模型观测点温度增长速度快于绝热模型,较早于后者达到销蚀应变,被删除;1 750 m/s时结果与900 m/s时正好相反。这是因为低速时弹头压力低(图8),单元应变率低,应变达到销蚀值所经历的时间长,弹头由于塑性变形产生的高热量有着较长的时间向后扩散,以致传入后方单元的热量多于后方单元传出的热量,使得该单元含有的热量高于绝热模型,高速情况下与之相反。

4 结 论

将热传导因素引入冲击动力学程序,对典型长杆弹侵彻陶瓷靶的过程进行数值计算,将计算结果与采用绝热模型得到的计算结果进行比较,发现长杆弹着速由低到高变化时,热传导对侵深的影响不同:长杆弹着速为900～1 350 m/s时,由于热传导模型弹销蚀速度较快,其计算侵深小于绝热模型计算结果;长杆弹着速为1 350～1 450 m/s时,两种模型弹销蚀速度接近,所以计算侵深接近;长杆弹着速为1 450～1 800 m/s时,热传导模型弹销蚀速度慢于绝热模型,其计算侵深大于后者计算侵深。由数据对比发现热传导模型计算侵深随着速的变化规律与实验数据更接近,这说明侵彻过程中考虑热传导因素所得结果更合理可信。本研究改善了传统侵彻计算中忽略热传导的状况,可为相关研究提供参考。

[1] 李永池,袁福平,胡秀章,等.卵形头部弹丸对混凝土靶板侵彻的二维数值模拟[J].弹道学报,2002,14(1):14-19. Li Yongchi,Yuan Fuping,Hu Xiuzhang,et al.The 2-D numerical simulation on penetrations of an oval headed projectile into concrete targets[J].Journal of Ballistics,2002,14(1):14-19.

[2] 晏麓晖,冯兴民,夏清波,等.应变率和绝热软化对空腔膨胀影响的数值模拟[J].国防科技大学学报,2011,33(3): 44-47. Yan Luhui,Feng Xingmin,Xia Qingbo,et al.A numerical simulation of the effects of strain rate and adiabatic softening on the Cavity Expansion Model[J].Journal of National University of Defense Technology,2011,33(3):44-47.

[3] 赵攀峰,沈兆武,孙宇新.含损伤热塑性材料靶板的抗冲塞研究[C]∥第十届全国激波与激波管学术讨论会论文集, 2002:141-146.

[4] Ning Jianguo,Ren Huilan,Guo Tingting,et al.Dynamic response of alumina ceramics impacted by long tungsten projectile[J].International Journal of Impact Engineering,2013,62:60-74.

[5] Lidén E,Mousavi S,Helte A,et al.Deformation and fracture of a long-rod projectile induced by an oblique moving plate:Numerical simulations[J].International Journal of Impact Engineering,2012,40/41:35-45.

[6] Iqbal M A,Gupta G,Diwakar A,et al.Effect of projectile nose shape on the ballistic resistance of ductile targets [J].European Journal of Mechanics—A/Solids,2010,29(4):683-694.

[7] 孙宇新,李永池,于少娟,等.长杆弹侵彻受约束A95陶瓷靶的实验研究[J].弹道学报,2005,17(2):38-41. Sun Yuxin,Li Yongchi,Yu Shaojuan,et al.An experimental study on the penetration confined A95 ceramic targets[J].Journal of Ballistics,2005,17(2):38-41.

[8] 孙宇新,张进,李永池,等.内爆加载下热塑性管壳的应力波演化与层裂效应研究[J].高压物理学报,2005,19(4): 319-324. Sun Yuxin,Zhang Jin,Li Yongchi,et al.Propagation of stress wave and spallation of cylindrical tube under external explosive Loading[J].Chinese Journal of High Pressure Physics,2005,19(4):319-324.

[9] 李硕,王志军,徐永杰,等.热处理对弹体材料侵彻能力影响的分析[J].兵工学报,2014,35(S2):78-82. Li Shuo,Wang Zhijun,Xu Yongjie,et al.The effect of heat treatment on penetration performance of projectile material[J].Acta Armamentarii,2014,35(S2):78-82.

[10] 赵晓宁,何勇,张先锋,等.A3钢抗高速杆弹侵彻的数值模拟与实验研究[J].南京理工大学学报,2011,35(2):164-167. Zhao Xiaoning,He Yong,Zhang Xianfeng,et al.Experimental and numerical study on A3 steel targets penetrated by high-velocity long-rod projectiles[J].Journal of Nanjing University of Science&Technology,2011,35(2): 164-167.

[11] 卞梁,王肖钧,章杰.SPH/FEM耦合算法在陶瓷复合靶抗侵彻数值模拟中的应用[J].高压物理学报,2010,24 (3):161-167. Bian Liang,Wang Xiaojun,Zhang Jie.Numerical simulations of antipenetration of confined ceramic targets by SPH/FEM coupling method[J].Chinese Journal of High Pressure Physics,2010,24(3):161-167.

[12] 杨震琦,庞宝君,王立闻,等.JH-2模型及其在Al2O3陶瓷低速撞击数值模拟中的应用[J].爆炸与冲击,2010,30 (5):463-471. Yang Zhenqi,Pang Baojun,Wang Liwen,et al.JH-2 model and its application to numerical simulation on Al2O3ceramic under low-velocity impact[J].Explosion and Shock Waves,2010,30(5):463-471.

[13] 任会兰,陈雯,郭婷婷.陶瓷靶抗侵彻特性的数值模拟研究[J].北京理工大学学报(自然科学版),2013,33(2):111-115. Ren Huilan,Chen Wen,Guo Tingting.Numerical simulation on the anti-penetration properties of ceramic target [J].Transactions of Beijing Institute o Technology(Natural Science Edition),2013,33(2):111-115.

Influence of heat transfer on long-rod projectiles penetrating into ceramic targets

Li Ruiyu1,Sun Yuxin1,Zhou Ling2,Sun Qiran1, Zhao Yayun1,Feng Jiangtuo1
(1.National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China; 2.China Academy of Ordnance Science,Beijing100000,China)

Based on the finite element method,the heat conduction equation was made discrete and written as the heat transfer computation code which was then embedded into the existing impact dynamics program.The new program was applied to the numerical analysis of the long-rod projectile penetrating into AD95 ceramic targets in the range of 900-1 800 m/s,and the influence of heat transfer on penetration capability was examined.Calculations show that the calculated penetration depth is less than that by the adiabatic model when the heat transfer is taken into account in the range of 900-1 350 m/s.However,it is opposite when the velocity of the projectile comes in the range of 1 450-1 800 m/s.The results by the heat transfer model and the adiabatic model are close to each other in the range of 1 350-1 450 m/s.

penetration;heat transfer;finite element;ceramic

O385国标学科代码:13035

:A

10.11883/1001-1455(2017)02-0332-07

(责任编辑 张凌云)

2015-09-25;

:2016-03-23

李芮宇(1991— ),男,博士研究生;

:孙宇新,yxsun01@163.com。