气相爆轰波传播过程中的自点火效应*

张 薇,刘云峰,滕宏辉,姜宗林

(中国科学院力学研究所高温气体动力学国家重点实验室,北京100190)

气相爆轰波传播过程中的自点火效应*

张 薇,刘云峰,滕宏辉,姜宗林

(中国科学院力学研究所高温气体动力学国家重点实验室,北京100190)

基于基元反应模型和单步反应模型,对直管道中H2-air混合气体中爆轰波的传播过程进行了数值模拟,揭示了气相爆轰波传播过程中的自点火效应。利用数值模拟方法计算了不同爆轰模型的点火延迟时间,并得到了爆轰波三波点的传播过程以及所形成胞格结构的尺寸。结果表明,胞格宽度与点火延迟时间成正比;爆轰波诱导区内气体的点火延迟时间与三波点的运动周期基本一致。进一步对结果分析可知,爆轰波的自维持传播取决于点火延迟时间(表征化学反应的特征时间)和三波点的运动周期(表征流动的特征时间)的匹配;当二者相匹配时,经过前导激波压缩后形成的高温高压爆轰气体,在短时间内实现了自点火,同时释放出大量的能量推动了爆轰波的前进,即爆轰波的稳定自维持传播依靠其自点火机制。

胞格爆轰波;自点火;点火延迟时间;三波点

爆轰波是一种以高超声速传播的燃烧波。经过前导激波压缩的可燃气体,在非常短的时间和距离内完成自点火过程,通过化学反应释放大量的热,推动爆轰波继续前行,完成爆轰波的自维持传播。因此,爆轰波研究中最本质、最基础的研究是关于爆轰波自维持传播机理的研究[1-5]。

现有研究多从爆轰波复杂的波系结构以及激波动力学角度出发,定性分析爆轰波传播过程中不同物理因素的作用。V.N.Gamezo等[6]采用单步反应模型对爆轰波进行数值模拟,研究指出,波后未反应区域的爆炸推动了爆轰波的前进,其形成取决于活化能,而横波的相互碰撞使得中间部分的未反应区域燃烧更快。G.J.Sharpe[7]研究了爆轰波传播过程中横波的发展和运动情况,使用不同的网格分辨率分析横波的碰撞以及波后未反应袋中燃烧速率对网格的敏感度,研究指出,在分析爆轰波的波系结构时,除高效优化的网格以外,还要处理好反应中的时间、空间尺度之间的匹配关系,尤其在化学反应时间很短的情况,准确捕捉波面结构更为重要。J.Y.Choi等[8]总结了不同的化学反应模型对爆轰波胞格的影响,讨论了边界条件、计算域长度、时间步长、网格尺度等因素对胞格宽度数值模拟结果的影响,并且定性分析了活化能和反应的指前系数对稳定与不稳定爆轰波传播的影响。

爆轰波的传播涉及到非线性与多尺度的三维复杂流动过程。实验中,通过烟熏法以及瞬态流场捕捉技术可以得到三维爆轰波面传播所留下的鱼鳞状胞格结构。爆轰波传播过程中,前导激波由多个间隔排列的马赫杆、入射激波和横波组成。马赫杆、入射激波和横波相交于三波点,并形成三波结构,三波点的运动轨迹即为胞格结构。爆轰现象包含复杂的激波动力学与化学反应过程,胞格结构是这一过程的外在表现,最能够反映爆轰波传播的重要特征[9]。近年来,已经利用理论、实验以及数值模拟方法开展了大量关于胞格结构的研究工作。实验研究是通过爆轰波在激波管中的传播,通过不同的测量仪器和手段记录三波点的轨迹以及瞬时的波系结构;数值模拟和理论分析则多是考虑多种因素,如活化能、指前系数、边界条件以及网格尺度等,对胞格大小的定性影响。对于胞格的定量化研究,现有理论均从反应区长度入手,将ZND模型理论计算所得半反应区长度与实验测得的胞格大小做线性拟合,针对特定配比的反应物得到特定的拟合公式。反应区的特征长度能和胞格的大小联系在一起,其中一定存在重要的物理机理。但是,拟合公式却没有普适性,不能说明线性关系存在的原因。

现有理论表明,爆轰波传播过程的主要机制在于非线性波与化学反应带的耦合[10-12]。燃烧理论中,在高温热化学环境下,自点火机制扮演着重要的角色[13]。火焰的稳定性主要由化学反应模型控制[13]。本研究从胞格的大小出发,通过对不同化学反应模型的数值模拟结果的比较,分析自点火机制在爆轰波传播过程中的作用,讨论非线性波与化学反应带的关键耦合参数,从爆轰波传播过程中的耦合机理出发,探讨其中的关键物理机制,指出影响胞格大小的关键因素及其根本原因。

1 控制方程与模型

爆轰波在二维无限长的直管道中传播,上、下边界满足反射壁面边界条件,计算域见图1。左侧为高温高压点火区,爆轰波从左向右传播;初始爆轰气体为满足化学当量比的H2-air混合气体,初始压力p0=0.1 MPa,初始温度T0=300 K,当量比ϕ=1.0。为保证爆轰波传播足够长的时间,在数值模拟过程中,保证声速点以及稀疏波完整的前提下,计算区域在计算过程中不断右移,使得计算区域足够大,即爆轰波能够在足够长的管道中传播直至达到稳定状态。由于流场中含有化学反应,流动方程组需要与化学反应动力学模型耦合起来数值求解,计算过程中的“刚性问题”和计算效率问题都会影响到计算所需的计算机内存和CPU时间,本研究在程序中加入并行计算Open MP(Open Multiprocessing),在保证网格尺度和网格数目的前提下,使得计算效率大大提高。每个数值算例中的爆轰波的总传播时间都在毫秒量级,以保证胞格尺度统计的可靠性。

图1 计算模型示意图Fig.1 Schematic illustration of the problem considered

控制方程为二维Euler方程组,忽略了爆轰波传播过程中的扩散效应、粘性效应和热传导过程。化学反应采用一个修正的总包单步反应模型[12,14]和一个共包含9组元、19个反应的基元反应模型[15]。式(1)～(7)为单步反应模型控制方程,基元反应模型的详细反应参数参见文献[15]。

式中:p、ρ、u、v、e、γ、q和Z分别表示压力、密度、轴向速度、横向速度、比内能、比热比、混合气体的比放热量和化学反应进行度参数;源项中的˙ω表示爆轰产物的质量生成率;在化学反应速率的阿伦尼乌斯(Arrhenius)公式中,K、T、Ea和R分别为指前系数、温度、活化能和气体常数;式(5)～(7)中的下标“U”代表反应物,下标“B”代表生成物。单步反应模型的参数取值如表1所示。

表1 单步反应模型的参数取值Table 1 Parameters of one-step reaction model

在数值模拟中,在空间方向上采用三阶的ENO格式离散,对矢通量进行了Steger-Warming分解。在时间方向上采用三阶TVD Runge-Kutta法。在下面的结果与讨论中,首先研究两个模型的点火延迟时间,然后对二维爆轰波的胞格结构进行模拟。通过对三波点的形成与发展以及自点火过程的分析,给出激波动力学和化学反应耦合的关键机理。

2 结果与讨论

2.1 点火延迟时间

作为自点火过程中的重要参数,点火延迟时间表征了化学反应的特征时间,是化学反应模型的重要参数。点火延迟时间的定义有多种方法,本文基于温度变化来定义点火延迟时间:对于特定的化学反应模型,利用等容燃烧所得温度T随时间t的变化曲线,定义最大温度变化率(dT/d)tmax所对应的时间为点火延迟时间。对于稳定传播的爆轰波,诱导区内的气体热力学状态对自点火过程更为重要。准确预测与诱导区内气体温度T*和压力p*相对应的点火延迟时间对爆轰波的数值模拟是至关重要的。根据一维ZND模型,对于H2-air爆轰波,当初始压力p0=0.1 MPa和初始温度T0=300 K时,对应的诱导区内的气体温度和压力分别为T*=1544.1 K和p*=2.77 MPa。但是,在二维爆轰波的数值模拟中,爆轰波面更为复杂,波后诱导区内的气体状态分布是不均匀的,T*和p*分别在1 300～1 500 K和1.5～3.0 MPa范围内变化。

图2给出了总包单步反应模型(model-1)和基元反应模型(model-2)预测的初始压力为0.1 MPa下的点火延迟时间随温度的变化情况,同时还给出了部分实验结果作为对比。可以看出,在对数坐标下,在1 000～1 500 K(对应的横坐标取值范围为10.0～6.6 K-1)的高温下,爆轰模型预测的点火延迟时间随温度近似呈线性变化,实验结果也基本反映了该规律。点火延迟时间与温度成反比,温度越高,点火延迟时间越短。相同温度下,两个模型计算得到的点火延迟时间并不相同。两个模型预测的点火延迟时间曲线斜率不同,在T=1 200 K(横坐标取值为8.3)左右相交。在1 300～1 500 K的温度范围内(对应的横坐标取值范围为7.7～6.6 K-1),同一温度下,利用model-2计算得到的点火延迟时间比model-1要长,并且温度越高,差别越大,但是两者的差值在18μs以内。曲线的斜率表示点火延迟时间对温度的敏感程度,斜率越大,意味着点火延迟时间对温度变化越敏感。需要说明的是,model-1的计算结果是与压力无关的,即改变初始压力,对利用model-1计算得到的点火延迟时间没有影响。这是单步反应模型的重要特性,也是利用这类模型进行爆轰波数值研究时需要注意的事项。

图2 模型和实验预测的点火延迟时间对比Fig.2 Comparison of ignition delay times predicted by two models and the experimental data

与单步反应模型不同的是,基元反应模型的点火延迟时间是与压力相关的。图3给出了不同压力下利用Model-2计算得到的点火延迟时间,并将其与model-1的预测结果作比较。首先,比较在初始压力为0.1、1.0和2.0 MPa时model-2预测的点火延迟时间可知:在1 200～1 500 K的高温段(对应的横坐标取值范围为8.3～6.6),随着压力的增加,相同温度下的点火延迟时间逐渐减小,并且与压力基本呈线性反比变化,这是基元反应模型的重要特性。以T=1 300 K(横坐标取值为7.7)为例,model-1预测的点火延迟时间(τig)为19.82μs,且该数值不随压力变化。但是,对于model-2,当压力为0.1 MPa时,τig=30.90μs;当压力为1.0 MPa时,τig=3.00μs;当压力为2.0 MPa时,τig=1.00μs。压力越高,model-2预测的点火延迟时间就越短,相比于model-1预测结果,两者的差值可以达到一个数量级甚至更大。高温高压下的实验结果比较缺乏,因此无法与实验结果进行比较。

对于初始压力0.1 MPa、初始温度300 K、满足化学当量比的H2-air爆轰波,诱导区内温度和压力分别在1300～1500 K和1.5～3.0 MPa范围内,研究这一范围内的点火延迟时间更为重要。图4比较了初始压力为1.0 MPa时不同模型预测的点火延迟时间(除model-1和model-2的计算结果外,其他结果参见文献[16-17])。可以看出,对于基元反应模型来说,点火延迟时间在不同的温度区间对温度的敏感性是不同的,不同的反应模型在相同温度下的点火延迟时间都不相同,其差异甚至在一个数量级以上。在1 300～1 500 K的范围内,model-1的点火延迟时间比其他基元反应模型的结果都要长。

图3 不同压力下model-1和model-2的点火延迟时间Fig.3 Comparison of ignition delay times predicted by model-1 and model-2 at different pressures

图4 不同化学反应模型预测的点火延迟时间Fig.4 Comparison of ignition delay times predicted by different chemical reaction models

2.2 三波点的运动

利用model-1和model-2两个爆轰模型分别模拟了H2-air混合气体中稳定传播的爆轰波及其胞格结构。为使数值模拟结果具有可靠性,在不同网格分辨率和计算域大小的条件下开展了研究。网格尺度满足Δx=Δy,其取值为10或20μm;计算域宽度(w)取值为2、3、4、8或16 mm。计算区域足够长,以避免出口边界对爆轰波面的影响。爆轰波的数值模拟中,首先采用直接点火的方式,形成过驱爆轰波,过驱爆轰波逐渐衰减为稳定传播的CJ爆轰波。当爆轰波传播足够长的时间,三波点个数不再发生改变时,爆轰波即达到稳定传播的状态。本文对爆轰波传播过程的分析均针对达到稳定传播状态的爆轰波。

图5给出了利用model-1模拟所得稳定传播的爆轰波的流场压力分布,观察图5可得爆轰波波面三波点的个数:当w=4 mm时,波面上存在一个三波点;当w=8 mm时,有一对三波点;当w增加到16 mm时,有两对三波点。3种情况下,平均每8 mm的计算宽度,波面有一对三波点的存在,说明计算结果与网格数以及网格分辨率均无关,计算结果可靠。

一对三波点从一次碰撞开始到下一次碰撞为止,完成一个运动周期。经过两个运动周期的一对三波点,其运动轨迹形成一个完整的胞格。对于稳定传播的爆轰波,三波点运动周期是固定不变的。图6给出利用model-1模拟所得稳定传播的爆轰波三波点的运动情况,以计算域为w=8 mm为例说明了一对三波点在一个周期内的运动规律,其中每两幅图之间的时间间隔是2μs。从图6中可以看出,一对三波点完成一个完整胞格需耗时6μs,因此这一对三波点的运动周期则约为3μs。在诱导区内的气体的平均压力为1.9 MPa,平均温度为1 500 K左右。在该状态下,单步反应模型model-1预测的点火延迟时间为3.46μs(见图2)。由此可见,三波点的运动周期与诱导区内气体对应的点火延迟时间一致,其他算例也给出了同样的结论。

图5 采用model-1数值模拟二维爆轰波传播,流场的压力等值线Fig.5 Instantaneous contours of pressure for a two-dimensional detonation propagation simulated by model-1

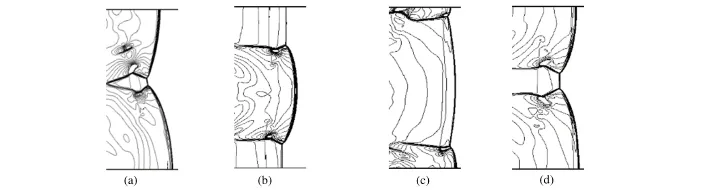
图6 采用model-1数值模拟的一对三波点的压力等值线分布Fig.6 Movement of triple-wave points shown with the pressure contour maps in the numerical simulation by model-1

图7给出了利用model-2模拟所得稳定传播的爆轰波的流场压力分布图。当w=2 mm时,波面上存在2对三波点;当w=3 mm时,为3对三波点;当w增加到4 mm时;波面上则有4对三波点。3种情况下,平均每1 mm的计算宽度,波面有一对三波点的存在,保证了计算结果的网格无关性。

图8为利用model-2模拟所得稳定传播的爆轰波三波点的运动情况。在计算域为w=3 mm的情况下,得到了3对三波点,其中每两幅图之间的时间间隔是0.1μs。从图8中可以看出,一对三波点运动完成半个胞格用时0.9μs,即这一对三波点的运动周期约为0.9μs。而在1.9 MPa、1 500 K时,基元反应模型model-2预测的点火延迟时间为0.94μs(见图2)。由此可见,三波点的运动周期与诱导区内气体对应的点火延迟时间一致。其他算例也给出了同样的结论。

图7 采用model-2数值模拟二维爆轰波传播,流场的压力等值线Fig.7 Instantaneous contours of pressure for a two-dimensional detonation propagation simulated by model-2

图8 采用model-2数值模拟的一对三波点运动的胞格结构Fig.8 Movement of triple-wave points shown with the cellular structure simulated by model-2

2.3 胞格结构

对于稳定传播的爆轰波的胞格结构,胞格尺度是指所有胞格的平均宽度。图9为利用model-1模拟得到的稳定的胞格结构。当w=4 mm时,垂直于爆轰波的传播方向上形成了半个胞格;当w=8 mm时,形成1个胞格;当w=16 mm时,形成2个胞格。所有3种计算条件下,平均胞格尺度均为8 mm,即计算结果的网格无关。实验测得的胞格尺度在8～15 mm之间[18],因此利用model-1模拟得到的胞格尺度与实验值完全一致。图10给出了利用model-2模拟得到的稳定胞格结构。从图10中可以看出:在w=2 mm的计算域中,垂直于爆轰波传播方向得到2个完整的胞格;当w=3 mm时,得到3个胞格;当w=4 mm时,胞格数增加到4个。胞格宽度同样与网格无关,利用model-2数值模拟得到的平均胞格宽度为1 mm,是model-1和实验所得胞格宽度的1/8。

通过以上分析可知,在诱导区温度为1 300～1 500 K、压力为1.5～3.0 MPa的范围内,model-1给出的点火延迟时间比model-2的结果要长,并且采用model-1计算得到的胞格比model-2的胞格更宽,说明点火延迟时间和胞格宽度成正比。另外,利用model-1所得点火延迟时间的斜率比model-2要大(见图2),其对应的自点火过程对温度变化就更为敏感;在相同的温度和压力变化下,斜率大的点火延迟时间变化范围更大,波面上各点的点火延迟时间相差也比较大,自点火过程相对更加不稳定,胞格更不规则。

图9 采用model-1数值模拟二维H2-air爆轰波的胞格结构Fig.9 Cellular structures for a two-dimensional H2-air detonation simulated by model-1

图10 采用model-2数值模拟二维H2-air爆轰波的胞格结构Fig.10 Cellular structures for a two-dimensional H2-air detonation simulated by model-2

现有模型预测的胞格尺度都比实验值至少小两倍[19],主要原因在于高温高压下的点火机制上存在问题。现在化学反应模型的参数设置是根据层流火焰速度与点火延迟时间的实验数据来确定的,而实验中不仅缺乏低温的结果,在高温高压的实验结果也是微乎其微,使得模型在预测高温高压下的点火机制时,有某些重要的物理机制被忽略或表达有误。当然,研究中使用的单步反应模型之所以能够准确的模拟胞格结构,主要在于该模型能够准确模拟当量比的H2-air混合气体在1.9 MPa和1 500 K下的点火延迟时间。实际上,model-1的点火延迟时间与压力无关,其胞格宽度也与压力无关,无论在什么初始压力条件下,模拟得到的胞格大小都是不变的,这一点与物理规律不符,需要引起注意。

上述研究结果表明,爆轰波波后诱导区的气体的压力、温度对应的点火延迟时间与三波点的运动周期一致。运动周期反映的是爆轰波的动力学特性,而点火延迟时间反映的是爆轰波的化学反应动力学特性,二者是通过同一个时间尺度耦合在一起的。从爆轰波传播的物理机制来看,首先,前导激波压缩混合气体,使其压力和温度升高达到可燃条件,经过该状态对应的点火延迟时间后,这部分气体开始燃烧,完成自点火过程。自点火中释放的大量的热量,推动爆轰波继续向前,完成激波和燃烧的耦合。这两个特征时间尺度的匹配就尤为重要。如果点火延迟时间过长,那么化学反应的能量释放太慢,就无法维持爆轰波的自维持传播;如果点火延迟时间过短,又会导致在三波点到达之前,不应该燃烧的气体提前燃烧,产生新的三波点,那么得到的胞格数量就会变多,胞格尺寸就会变小。只有二者相互匹配,才能够得到稳定的胞格结构,同时保证激波和化学反应带的耦合。前导激波压缩过的爆轰气体可以实现自点火,自点火过程释放的能量得以推动爆轰波继续传播,这就是气相爆轰波流动与化学反应的耦合机理。对于化学反应模型来说,为了准确地模拟爆轰波的传播过程,就要保证模型能够准确模拟关键状态下的点火延迟时间,再现自点火过程,并确保化学反应动力学和气体动力学的特征时间尺度完全匹配。

3 结 论

基于二维欧拉方程数值研究的爆轰波,采用基元反应模型和单步反应模型描述化学反应过程,对不同模型的点火延迟时间进行比较,同时统计了爆轰波在稳定传播的状态下,两个模型得到的胞格的宽度以及三波点的运动周期,研究结果表明:(1)爆轰波的胞格宽度与点火延迟时间成正比;(2)化学反应带中诱导区内气体对应的点火延迟时间等于三波点的运动周期,点火延迟时间是非线性波的特征时间,三波点的运动周期是化学反应带的特征时间,爆轰波传播过程中,非线性波和化学反应带通过特征时间这一关键参数耦合在一起,爆轰波依靠爆轰气体的自点火过程得以自维持传播。

[1] Lee J H S.The detonation phenomenon[M].Cambridge University Press,2008.

[2] 滕宏辉,吕俊明,姜宗林.可燃气体中激波与障碍物作用在下游形成爆轰波的数值研究[J].爆炸与冲击,2007,27 (3):251-258. Teng Honghui,LüJunming,Jiang Zonglin,et al.Downstream detonation initiation induced by interaction between shock wave and obstacle in combustible gas mixtures[J].Explosion and Shock Waves,2007,27(3):251-258.

[3] 滕宏辉.气相爆轰波形成和传播机制的基础问题研究[D].北京:中国科学院力学研究所,2008.

[4] 王昌建,徐胜利.直管内胞格爆轰的基元反应数值研究[J].爆炸与冲击,2005,25(5):405-416. Wang Changjian,Xu Shengli.Numerical study on cellular detonation in a straight tube based on detailed chemical reaction model[J].Explosion and Shock Waves,2005,25(5):405-416.

[5] 滕宏辉,张德良,李辉煌,等.用环形激波聚焦实现爆轰波直接起爆的数值模拟[J].爆炸与冲击,2005,25(6):512-518. Teng Honghui,Zhang Deliang,Li Huihuang,et al.Numerical investigation of detonation direct initiation induced by toroidal shock wave focusing[J].Explosion and Shock Waves,2005,25(6):512-518.

[6] Gamezo V N,Desbordes D,Oran E S.Two-dimensional reactive flow dynamics in cellular detonation waves[J]. Shock Waves,1999,9(1):11-17.

[7] Sharpe G J.Transverse waves in numerical simulations of cellular detonations[J].Journal of Fluid Mechanics, 2001,447:31-52.

[8] Choi J Y,Ma F H,Yang V.Some numerical issues on simulation of detonation cell structures[J].Combustion, Explosion,and Shock Waves,2008,44(5):560-578.

[9] Oran E S,Jones D A,Sichel M.Numerical simulations of detonation transmission[J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1992,436(1897):267-297.

[10] 姜宗林,滕宏辉.气相规则胞格爆轰波起爆与传播统一框架的几个关键基础问题研究[J].中国科学,2012,42(4): 421-435. Jiang Zonglin,Teng Honghui.Research on some fundamental problems of the universal framework for regular gaseous detonation initiation and propagation[J].Scientia Sinica,2012,42(4):421-435.

[11] Lee J H S.Dynamic parameters of gaseous detonations[J].Annual Review of Fluid Mechanics,1984,16(1):311-336.

[12] 张薇,刘云峰,姜宗林.气相爆轰波胞格尺度与点火延迟时间关系研究[J].力学学报,2014,46(6):977-981. Zhang Wei,Liu Yunfeng,Jiang Zonglin.Study on the relationship between ignition delay time and gaseous detonation cell size[J].Chinese Journal of Theoretical and Applied Mechanics,2014,46(6):977-981.

[13] Stankovic I,Merci B.Analysis of auto-ignition of heated hydrogen-air mixtures with different detailed reaction mechanisms[J].Combustion Theory and Modelling,2011,15(3):409-436.

[14] 刘云峰,姜宗林.详细化学反应模型中温度修正项特性研究[J].中国科学,2011,41(11):1296-1306. Liu Yunfeng,Jiang Zonglin.Study on the chemical reaction kinetics of detonation models[J].Scientia Sinica, 2011,41(11):1296-1306.

[15] Burke M P,Chaos M,Ju Y,et al.Comprehensive H2/O2kinetic model for high-pressure combustion[J].Inter-national Journal of Chemical Kinetics,2012,44(7):444-474.

[16] Hayashi A K.Fundamentals of hydrogen ignition and high pressure hydrogen jet auto-ignition[R].Belfast,Ireland:The 3rd European Summer School on Hydrogen Safety,2008.

[17] 赵真龙,陈正,陈十一.计算氢气/空气混合物着火延迟时间的相关函数[J].科学通报,2010(11):1063-1069. Zhao Zhenlong,Chen Zheng,Chen Shiyi.Correlations for the ignition delay times of hydrogen/air mixture[J]. Chinese Science Bulletin,2010(11):1063-1069.

[18] Shepherd J E.Detonation database[DB/OL].(2005-01-25)[2015-08-25].http://shepherd.caltech.edu/detn_db/ html/db.html

[19] Taylor B D,Kessler D A,Gamezo V N,et al.Numerical simulations of hydrogen detonations with detailed chemical kinetics[J].Proceedings of the Combustion Institute,2013,34(2):2009-2016.

Auto-ignition effect in gaseous detonation propagation

Zhang Wei,Liu Yunfeng,Teng Honghui,Jiang Zonglin
(State Key Laboratory of High Temperature Gas Dynamics,Institute of Mechanics,Chinese Academy of Sciences,Beijing100190,China)

In this paper,the auto-ignition mechanism in the gaseous detonation propagation of the stoichiometric H2-air detonable mixture in a straight tube was numerically studied using an overall onestep chemical reaction model and a detailed chemical reaction model based on the two-dimensional Euler equations.Meanwhile,the ignition delay times predicted by different models under different pressures and at different temperatures were compared and the propagation process of triple-shock points and the cell sizes were investigated.The results demonstrated that the cell sizes are proportional to the ignition delay times,and the ignition delay time in the induction zone is consistent with the average movement period of the triple-shock points.The leading shock compresses the detonable gas and then both the temperature and the pressure of the gas rise.The gas with high temperature and pressure soon finishes the process of auto-ignition,and a lot of heat is released during the ignition to maintain the detonation propagation,which means the auto-ignition mechanism ensures the self-sustained detonation propagation.The ignition delay time is considered as a chemical time scale characterizing the chemical reaction.The period of the movement of the triple-shock points is a characteristic time scale of shock dynamics.The coupling of these two time scales is a principal mechanism in gaseous detonation propagation.

cellular detonation;auto-ignition;ignition delay time;triple-shock points

O381国标学科代码:1303510

:A

10.11883/1001-1455(2017)02-0274-09

(责任编辑 王玉锋)

2015-08-25;

:2015-12-07

国家自然科学基金项目(11532014)

张 薇(1988- ),女,博士研究生;

:刘云峰,liuyunfeng@imech.ac.cn。