Mathematica模拟简谐振动的合成

陈大伟 斯小琴

(安徽建筑大学城市建设学院 安徽 合肥 238076)

Mathematica模拟简谐振动的合成

陈大伟 斯小琴

(安徽建筑大学城市建设学院 安徽 合肥 238076)

按照一维、二维相互垂直和三维相互垂直3种情形，运用Mathematica软件分别模拟了同频率和不同频率的简谐振动合成.直观地显示了不同情况下简谐振动合成的结果，不但可以加深学生对各种简谐振动合成的理解，还可以提高学生的学习兴趣.

简谐振动 Mathematica 合成

简谐振动[1～3]是振动的最基本、最简单的振动形式，是研究各种复杂振动的基础.依据傅里叶级数和傅里叶变换，各种复杂的振动都可以看作是若干个或是无限多个简谐振动的合成.在实际应用中，常常遇到一个物体同时参与两个或更多个振动的情况.

对于一些简单的简谐振动的合成，可以经过数学运算得到合成振动的表达式[4,5]，但多数情形下，振动合成问题比较复杂，合振动的表达式难于得到，对于其运动的轨迹和随时间而变化的规律更难于直观想象.为了直观地了解不同情形下简谐振动叠加后合成振动的特点，本文利用Mathematica数学软件[6,7]，对不同情形下的简谐振动的合成进行了仿真模拟[8～11]，直观地显示了合成后的振动情况.

1 一维简谐振动的合成

(1)同频率简谐振动的合成

两个简谐振动的表达式分别为

x1=A1cos(ωt+φ10)

x2=A2cos(ωt+φ20)

则其合振动为

x=x1+x2=Acos(ωt+φ0)

(1)

其中

A=[(A1cosφ10+A2cosφ20)2+

多个简谐振动xi=Aicos(ωt+φi0)，其合振动为

x=∑xi=Axcos(ωt+φx0)

(2)

其中

两个或多个一维同频率简谐振动合成，其合振动仍为简谐振动，其频率与分振动频率相同，轨迹为余弦(或正弦)曲线，如图1所示(实线为合振动).同频率同方向简谐振动的合成原理，对于讨论光波、声波以及电磁辐射的干涉和衍射有重要作用.

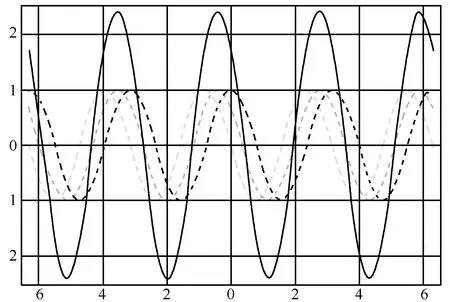
图1 3个一维同频率简谐振动合成的轨迹

(2)不同频率简谐振动的合成

一般情况下，同方向不同频率简谐振动的合成不再是简谐振动，而是复杂的振动.为突出频率不同引起的效果，文中只讨论同振幅、同相位、不同频率的简谐振动的合成.设两个简谐振动为

x1=Acos(ω1t+φ0)

x2=Acos(ω2t+φ0)

则合振动为

(3)

由式(3)可知，合振动不是简谐振动，而是以振幅

做周期变化的高频振动，其合振动周期称为“主周期”.若两个简谐振动的频率相差不大，即ω2+ω1≫ω2-ω1，则合振动是一个振幅随时间做周期性缓慢变化的高频振动，这种振幅时大时小的现象叫作拍.拍现象在光学、电磁学等领域都有重要应用，如用光拍法测光速.

多个简谐振动xi=Acos(ωit+φ0)，其合振动为

(4)

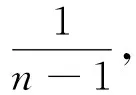
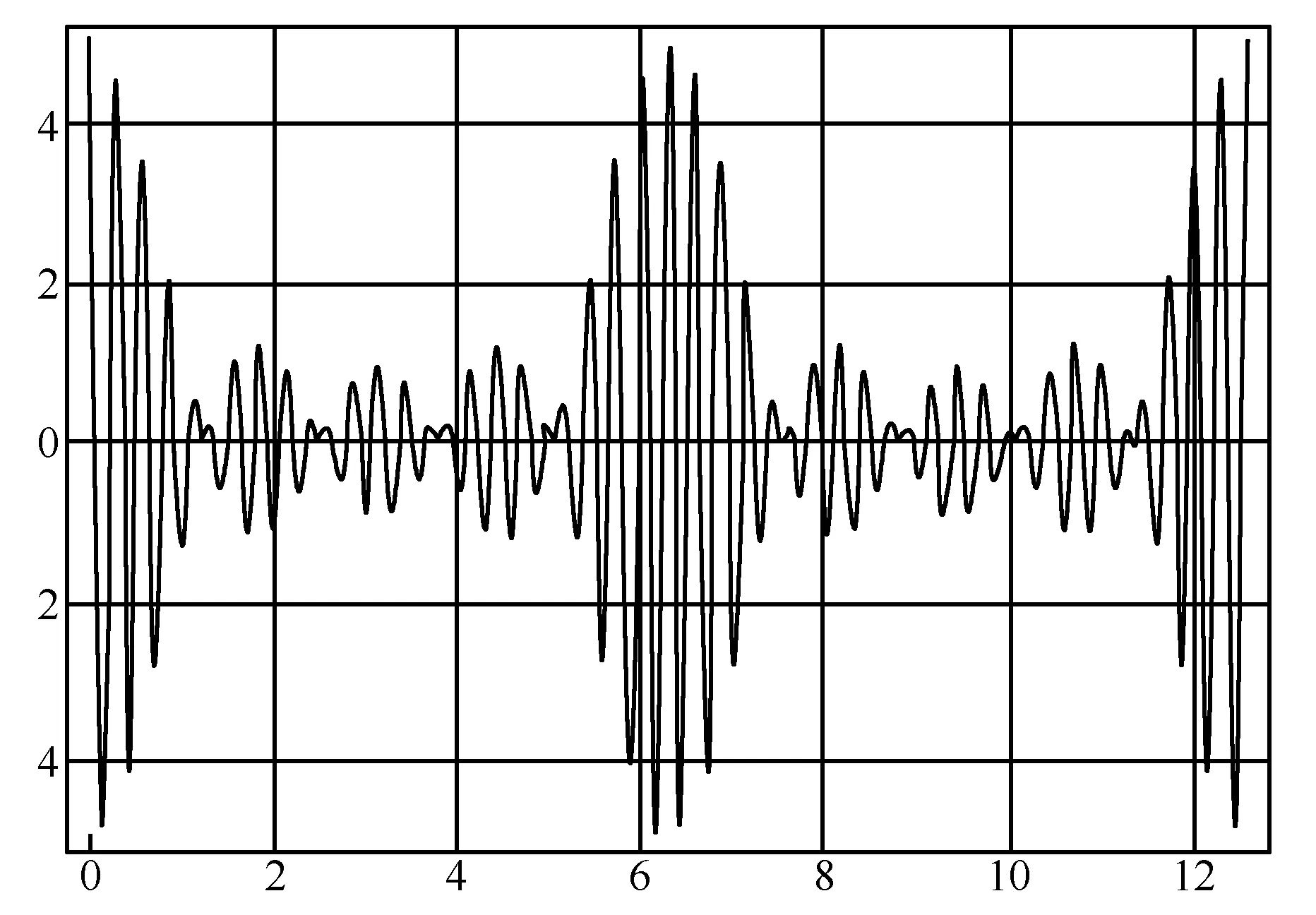
图2 5个一维不同频率简谐振动合成的拍现象

利用Mathematica仿真模拟可知，两个或多个一维频率比为有理数简谐振动的合振动虽然复杂但具有周期性,如图3实线所示，而频率比为无理数简谐振动的合振动则既复杂又无周期性，如图3虚线所示.

图3 4个一维简谐振动的合成

2 二维相互垂直的简谐振动合成

(1)同频率简谐振动的合成

设质点同时参与两个垂直方向上的简谐振动

x=A1cos(ωt+φ10)

y=A2cos(ωt+φ20)

从分振动方程式消去参数t，得合振动的轨迹方程为

(5)

多个二维简谐振动

x=∑xi=Axcos(ωt+φx0)

y=∑yi=Aycos(ωt+φy0)

其合振动为

(6)

由上式可知，二维相互垂直的同频率简谐振动的合振动的轨迹一般为椭圆，当相位差为零或π时为直线.轨道的具体形状、方位和运动方向由分振动的振幅和相位差决定，如图4所示.

图4 二维同频率简谐振动合成

(2)不同频率简谐振动的合成

一般来说，二维相互垂直的不同频率简谐振动，由于它们的相位差不是定值，其合振动的轨迹不能形成稳定的图案.但当它们的频率比为有理数时，则合成振动的轨迹能形成一封闭的稳定的曲线，曲线的花样和分振动的频率比、初相位有关，得出的图形叫李萨如图形，如图5(a)所示，而当频率比为无理数时，合振动的轨迹不能形成封闭的图形，如图5(b)所示.

图5 二维相互垂直不同频率的简谐振动的合成

3 三维相互垂直的简谐振动的合成

(1)同频率简谐振动的合成

设质点同时参与3个相互垂直方向上的简谐振动

x=A1cos(ωt+φ10)

y=A2cos(ωt+φ20)

z=A3cos(ωt+φ30)

则其合振动为

(7)

多个三维简谐振动

x=∑xi=Axcos(ωt+φx0)

y=∑yi=Aycos(ωt+φy0)

z=∑zi=Azcos(ωt+φz0)

其合振动为

(8)

三维相互垂直的同频率简谐振动的合振动与二维相互垂直同频率简谐振动的合振动相似，其合振动的轨迹为空间椭圆,如图6所示.

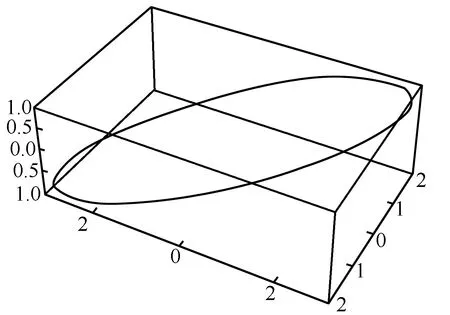
图6 三维同频率简谐振动合成

(2)不同频率简谐振动的合成

频率不同时，三维相互垂直的简谐振动，若频率比为有理数时，其合振动的轨迹能形成稳定的闭合曲线，如图7(a)所示.但当它们的频率比为无理数时，合成的轨迹不能形成闭合曲线，如图7(b)所示.

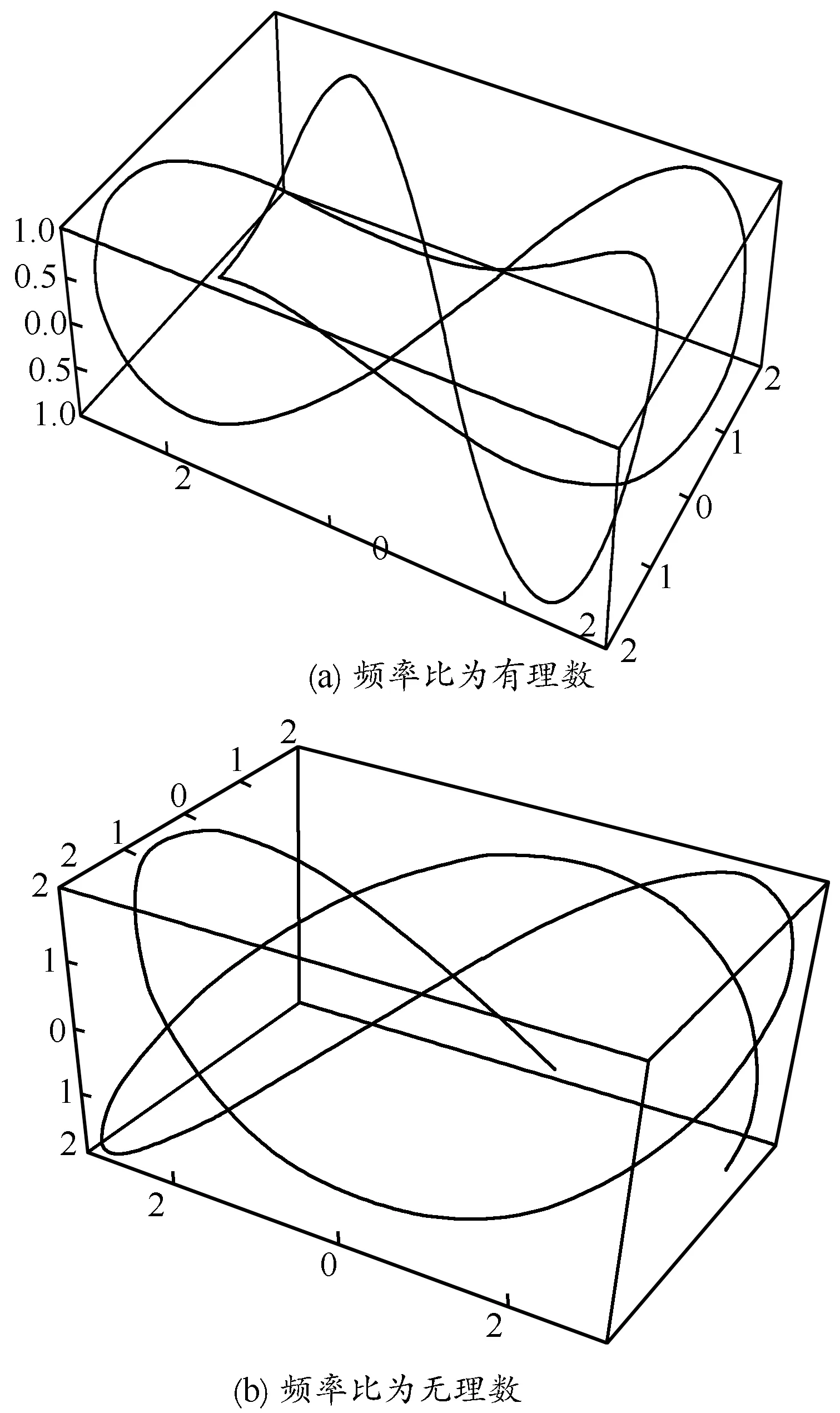
图7 三维相互垂直不同频率的简谐接动的合成

4 结束语

本文从振动的基本形式简谐振动出发，推导了各种情形的振动合成，并借助mathematica软件，对不同情形下的简谐振动的合成进行了仿真模拟，直观地显示了合成后的振动情况，有一定的参考价值.

1 赵近芳.大学物理学. 北京：北京邮电大学出版社, 2014.11

2 程守洙，江之永.普通物理学. 北京：高等教育出版社, 1999

3 漆安慎，杜婵英.普通物理学教程·力学.北京：高等教育出版社，1997.

4 蓝海江.多个简谐振动的合成.广西科学院学报，2009，25(1)：22～25

5 康文秀.同频率相互垂直简谐振动的合成.物理与工程，2005，15(6)：26～31

6 梁明华，樊东红，蓝丹.基于Mathematica三维图形的制作.贵州学院学报，2008，24(2)：128～130

7 阳明盛，林建华. Mathematica基础及数学软件. 大连：大连理工大学出版社, 2003

8 王宁星.拍图形的对称性.广州大学学报(自然科学版)，2002，1(5)：89～91

9 杨继先.相互垂直的谐振动合成轨迹研究.西华大学学报(自然科学版)，2008，27(2)：76～78

10 向根祥，石玉军.简谐振动合成的计算机模拟. 兰州文理学院学报(自然科学版)，2015，29(1)：25～28

11 王颖辉.同方向同频率谐振动合成初相位的确定.物理与工程，2010，20(3)：14～16

Simulation on the Synthesis of Harmonic Vibration Using Mathematica

Chen Dawei Si Xiaoqin

(Urban Construction College, Anhui Jianzhu University, Hefei,Anhui 238076)

In this paper, three cases are given of one dimensional, two dimensional and three dimensional, using mathematica to simulate the same frequency and different frequency synthesis of harmonic vibration. To display the different conditions of the synthesis of harmonic vibration results , not only can deepen students′ understanding of the synthesis of various harmonic vibration, but also can improve the students' interest in learning.

harmonic vibration; mathematica; synthesis

2016-10-31)