地震作用下高层结构重叠分散H∞控制鲁棒性研究

杨超亚, 汪 权, 王建国

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

地震作用下高层结构重叠分散H∞控制鲁棒性研究

杨超亚, 汪 权, 王建国

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章针对地震作用下高层建筑结构振动控制的鲁棒性问题,将集中H∞控制理论与多重叠分散控制理论相结合导出重叠分散H∞控制算法；采用该算法将20层钢结构Benchmark结构模型分别划分为2、4、8个子结构进行数值计算与分析,比较当结构刚度变化+15%和-15%时的控制效果。结果表明,当结构刚度在一定范围变化时,重叠分散H∞控制算法可以有效地抑制结构地震反应,控制效果不仅接近传统的集中控制方法,而且提高了高层结构大系统分散控制的鲁棒性。该算法可应用于大尺度高层结构振动控制中,实现高层建筑结构地震反应的可靠控制。

高层建筑;地震作用;重叠分散控制;鲁棒性

0 引 言

鲁棒性的概念于20世纪60年代被提出,目前在系统控制等领域得到广泛应用。鲁棒性指系统在内部不确定性因素影响和外部环境干扰下仍能保持稳定工作的能力。在实际的建筑结构振动控制中,建筑结构的模型参数(例如结构的阻尼和刚度)难以用数学模型来精确描述,结构的不确定性会导致系统控制的不稳定和控制性能恶化,因此,研究对结构参数和外部扰动具有较好鲁棒性、调节简单的控制算法是土木工程结构振动控制研究的一个重要方向[1]。

文献[2]考虑一维地震动作用和结构参数不确定性的影响,提出了一种基于线性矩阵不等式(linear matrix inequalities,LMI)的鲁棒H∞控制方法;文献[3]对变化的非线性系统的鲁棒无源性、反馈无源化和总体的鲁棒稳定性提出了新的控制方法;文献[4]研究了考虑建筑结构动力特性具有不确定性的多目标鲁棒H2/H∞控制问题;文献[5]通过设置特殊矩阵的方式,提出了一种基于建筑物相邻4层信号的鲁棒分散控制方法;文献[6]针对地震作用下的结构,采用包含原理设计了重叠(多重叠)控制器,对某5层框架结构进行了数值模拟。上述研究成果在鲁棒性和分散控制上有所贡献,但是未将控制算法应用于高层结构。文献[7]将模糊逻辑理论与遗传算法原理相结合提出分散遗传-模糊控制算法；文献[8-9]对重叠分散控制做了进一步研究,并对20层框架结构进行了数值模拟,都取得了满意的振动控制效果；文献[7-9]虽然将控制算法应用于高层结构,但是未考虑建筑结构模型参数的不确定性。

本文从结构振动控制鲁棒性出发,基于H∞理论与多重叠分散理论相结合导出重叠分散的H∞鲁棒控制方法,并对20层Benchmark建筑结构模型进行数值模拟与分析,将结构分别划分为2、4、8个子结构,比较当结构刚度变化+15%和-15%时的控制效果。

1 基本理论

1.1 分散控制系统模型

考虑线性连续时不变系统的状态空间模型S,即

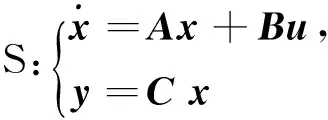
(1)

其中,x、u、y分别为系统S的状态向量、输入向量和输出向量,x∈Rn,u∈Rm,y∈Rl。

(2)

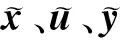
(3)

1.2 H∞控制算法

考虑一类线性时不变系统S的方程为：

(4)

其中,x(t)为状态向量,x(t)∈Rn;u(t)为控制力输出向量,u(t)∈Rp;w(t)为干扰输入向量;y(t)为观测输出向量,y(t)∈Rq;z(t)为控制输出向量,z(t)∈Rn；A、B、E、Cy、Cz、Dz为已知的、真实连续合适维数的矩阵。对于一个给定的输出反馈控制率u(t)=Gy(t),G为增益矩阵,(4)式可转化为:

(5)

从干扰w(t)到控制输出z(t)的闭环转换函数为:

(6)

其中，s为系统的零点。

(7)

定理1 考虑(4)式中的线性连续时间系统S,对于给定的γ>0,假定存在矩阵X>0及矩阵W,满足线性矩阵不等式,输出反馈控制器u(t)=Gy(t)使具有H∞有界范数γ的闭环系统(5)式是渐进稳定的。线性矩阵不等式为：

(8)

其中,*代表对称部分;X为对称正定矩阵,X∈Rn×n;W=GCyX。

推论1 在定理1中,若γ>0使(8)式可解,则(9)式的最优化问题是可行的。

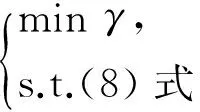
(9)

1.3 静态输出的反馈控制方法

为了获得(4)式所示系统S的输出反馈控制器u(t)=Gy(t),有必要分离出增益矩阵G。

首先寻找一个满秩的n×(n-q)维矩阵Qy,使得CyQy=0。求解(8)式的线性矩阵不等式,设

(10)

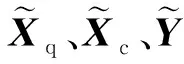
(11)

1.4 重叠分散静态反馈H∞鲁棒控制算法

(12)

其中,i=1,2,…,N;2≤N≤n-1。

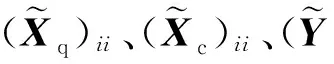
(13)

(14)

1.5 重叠分散H∞控制器设计

其中,ζ为输出矩阵系数。

图1 子系统划分工况

例如,将整个建筑结构振动控制系统扩展后解耦为4个子系统,如图2所示。

图2 4个子系统的重叠分解

图2中第5、10、15层的信息为2个子系统所共享。对4个子系统分别设计独立的H∞控制器,由参数最优化比较可得ζ=10-7.9时经济性最好,限于篇幅,此处不赘述。

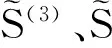
同理,可以得出2个子系统和8个子系统的情况。

2 算 例

本文将导出的重叠分散H∞控制方法应用于Benchmark控制问题,研究的对象是按照美国加州规范设计的钢结构,模型平、立面图参见文献[1]。为了分析方便,采用静力缩聚法对原有限元模型进行降阶,缩聚结构模型的楼层质量和刚度参数参见文献[10]。地震激励选用El Centro(NS,1940)波,将其峰值调整为5 m/s2,持时30 s,采样步长0.02 s。将结构划分为2、4、8个子结构,依次记为OD2、OD4和OD8。本文采用Matlab进行数值仿真,计算各个工况下的地震响应,并与集中H∞控制算法[7]相比较。

为说明重叠分散H∞控制算法的鲁棒稳定性,考察当结构刚度变化时其控制效果。选取20层Benchmark模型作为“基准建筑物”,并考虑2个附加的建筑物:一个为刚度高于基准建筑15%的“+15%建筑”,将基准建筑的刚度矩阵乘以1.15的系数得到其刚度矩阵;另一个为刚度低于基准建筑15%的“-15%建筑”,同理可得其刚度矩阵。将重叠分散H∞控制算法应用于这些建筑,可得出在地震作用下,各工况下不同刚度的结构振动控制地震响应,如图3～图8所示。可以看出，各子结构划分工况都可以有效地减小结构的地震响应,控制效果不仅接近传统的集中H∞控制,而且提高了高层结构分散控制的可靠性。由(7)式得OD2、OD4和OD8的控制指标γG分别为4.42、4.18和4.24,因此划分为4个子结构时为较优划分。

各控制算法结构位移和加速度反应峰值分别见表1、表2所列。从表1、表2可以得出,对于基准建筑,OD2的位移控制效果达77%～94%,加速度控制效果达28%～77%。对于ΔK=+0.15K建筑,位移控制效果达77%～93%,加速度控制效果达30%～74%;对于ΔK=-0.15K建筑,位移控制效果达78%～93%,加速度控制效果达28%～78%。同理,可以得出OD4、OD8在基准建筑、ΔK=+0.15K建筑、ΔK=-0.15K建筑下的位移和加速度控制效果。

上述数值模拟结果表明,当结构刚度变化+15%和-15%时,不同的子结构划分工况控制效果都很接近,说明重叠分散H∞控制算法具有良好的鲁棒性。

图3 基准建筑最大层间位移 图4 基准建筑最大加速度

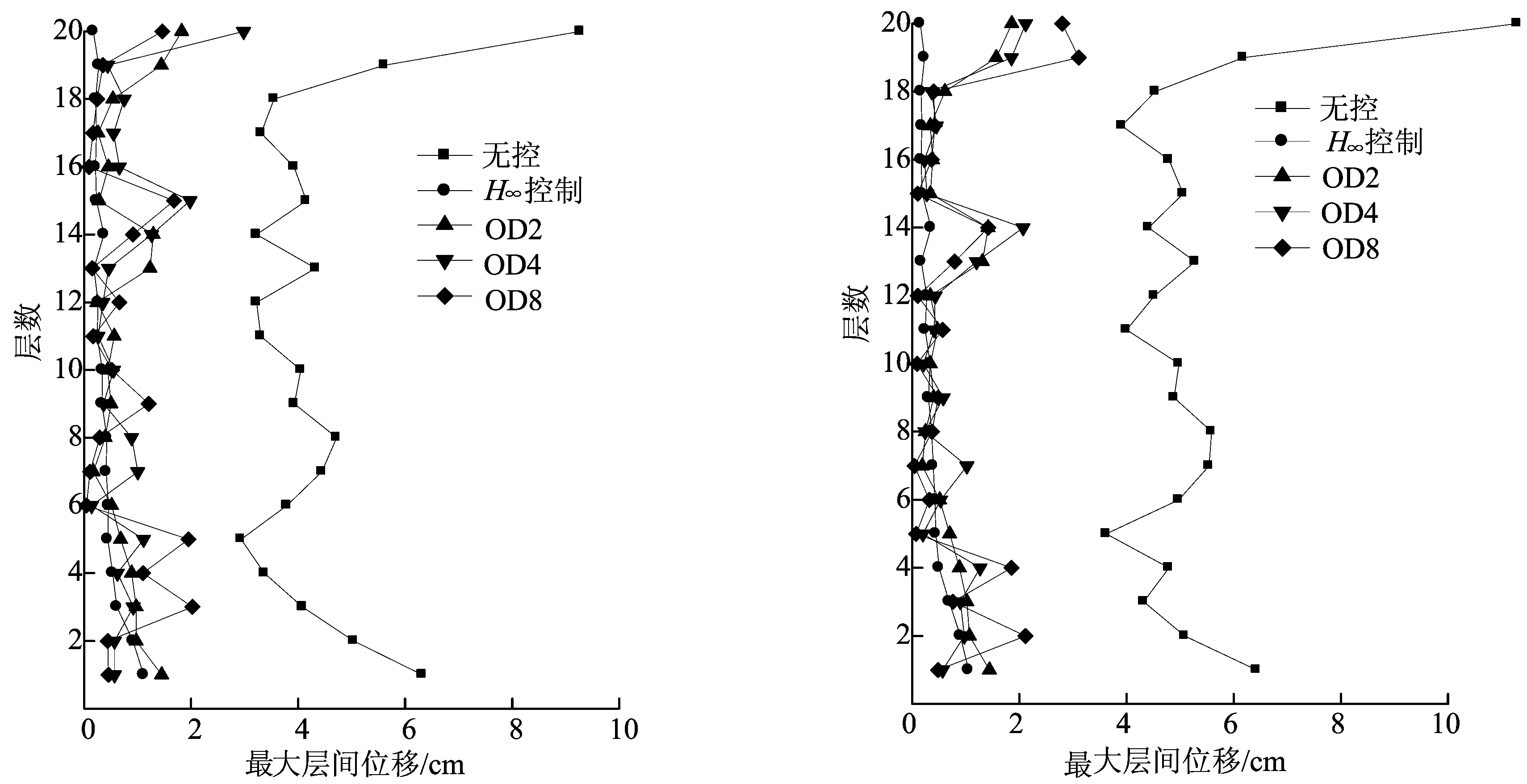
图5 ΔK=+0.15K时建筑最大层间位移 图6 ΔK=-0.15K时建筑最大层间位移

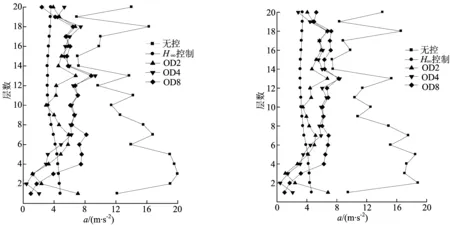
图7 ΔK=+0.15K时建筑最大加速度 图8 ΔK=-0.15K时建筑最大加速度 表1 不同控制算法在第1、5、10、15、20层处结构位移反应峰值比较

cm

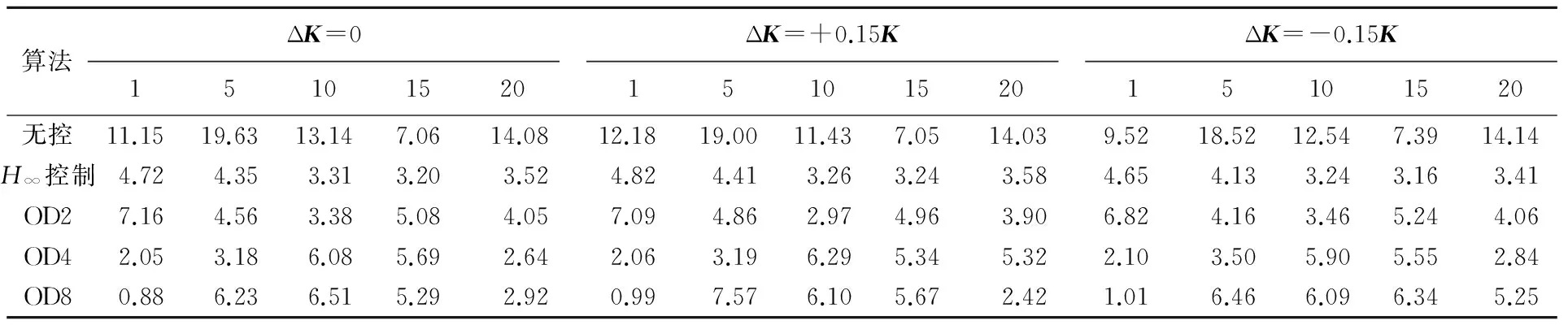
表2 不同控制算法在第1、5、10、15、20层处结构加速度反应峰值比较 m/s2

3 结 论

本文从高层建筑结构振动控制的鲁棒性出发,基于集中H∞控制理论与多重叠分散理论相结合导出重叠分散的H∞鲁棒控制方法,并对20层Benchmark建筑结构模型进行数值模拟与分析,给出了3种子结构划分工况的控制效果,与全状态输出H∞集中控制以及无控制情况相比较;结果表明本文方法可以作为抑制地震响应的有效方法。同时将提出的多重叠分散H∞控制算法,用于考虑结构刚度不确定性对结构鲁棒控制影响,证明其具有良好的鲁棒性,可以用于高层建筑的地震反应控制中。

[1] 欧进萍.结构振动控制:主动、半主动和智能控制[M].北京:科学出版社,2003:10-100.

[2] 李志军,王社良.建筑结构基于LMI的鲁棒非脆弱H∞控制[J].工程力学,2013,30(4):204-210.

[3] PANG Hongbo,ZHAO Jun.Robust passivity,feedback passification and global robust stabilisation for switched non-linear systems with structural uncertainty[J].IET Control Theory & Applications,2015,9(11):1723-1730.

[4] 宁响亮,刘红军,谭平,等.基于LMI的结构振动多目标鲁棒H2/H∞控制[J].振动工程学报,2010,23(2):167-172.

[5] 蒋扬,周星德,王玉,等.建筑结构鲁棒分散控制方法研究[J].振动与冲击,2012,31(6):37-41.

[7] 汪权,王建国,陈涛,等.高层建筑结构地震反应的分散遗传-模糊控制研究[J].合肥工业大学学报(自然科学版),2012,35(9):1230-1234.

[8] 康小方,王建国,许庆虎.建筑结构振动系统的多重叠分散静态输出反馈H∞控制方法[J].计算力学学报,2015,32(1):53-58.

[9] 汪权,庄嘉雷,张俊,等.地震作用下高层建筑结构的重叠分散控制研究[J].计算力学学报,2015,32(1):48-52.

[10] 王建国,汪权,张鸣祥.结构地震响应线性二次型最优迭代学习控制[J].应用科学学报,2010,28(2):197-202.

(责任编辑 张淑艳)

Robustness research on overlapping decentralizedH∞control of tall buildings under earthquakes

YANG Chaoya, WANG Quan, WANG Jianguo

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

In view of the robustness problem of vibration control of tall buildings under earthquakes, by combining the centralizedH∞control and multi-overlapping decentralized control strategies, an algorithm named overlapping decentralizedH∞control is derived. A typical 20-floor seismically excited Benchmark building is used for analyzing the performance of the control strategy. The building is divided respectively to two, four and eight substructures, and their control effects are compared when the structural stiffness increases 15% or decreases 15%. The results indicate that the overlapping decentralizedH∞control strategy can weaken the structural seismic response as effectively as the centralized control strategy. But the former is superior in guaranteeing the system’s robustness. When applied in vibration control, the strategy can achieve a reliable control of the seismic action on tall buildings.

tall building; seismic action; overlapping decentralized control(ODC); robustness

2015-12-10；

2016-01-19

国家自然科学基金资助项目(51408178);土木工程防灾减灾安徽省工程技术研究中心资助项目(教秘[2007]368号)

杨超亚(1992-),男,安徽岳西人,合肥工业大学硕士生; 王建国(1954-),男,安徽怀宁人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.02.015

TU973.31

A

1003-5060(2017)02-0215-06