改进极大似然估计大气湍流图像复原算法

张丽娟， 邱 欢， 殷婷婷， 刘 颖

(1.长春工业大学 计算机科学与工程学院， 吉林 长春 130012;2.吉林财经大学 管理科学与信息工程学院， 吉林 长春 130117)



改进极大似然估计大气湍流图像复原算法

张丽娟1， 邱 欢1， 殷婷婷1， 刘 颖2

(1.长春工业大学 计算机科学与工程学院， 吉林 长春 130012;2.吉林财经大学 管理科学与信息工程学院， 吉林 长春 130117)

采用Zernike多项式进行波前复原，并作为点扩散函数的初值，结合图像先验信息和参数估计改进最大似然估计法，对模拟的湍流退化图像进行复原实验。实验结果表明，相比于Lucy-Richardson和盲卷积算法，该算法复原后图像的灰度平均梯度有明显提高。

大气湍流； 自适应光学； 波前复原； 点扩散函数； 极大似然估计

0 引 言

自适应光学(Adaptive Optics， AO)系统在成像过程中受大气湍流效应影响，光波折射率会在传播路径中发生随机变化，使波前产生严重畸变，导致观测到的目标图像模糊或退化[1]。由于系统结构及CCD噪声等因素的影响，AO系统只能对波前进行部分校正，此时观测到的目标图像质量仍然很不理想。因此，需要对湍流退化图像进行后续复原处理来弥补AO系统对波前的校正误差，提高目标图像分辨率。Ayers[2]等于1988年提出了单帧迭代的盲卷积算法，并应用在湍流图像复原中[3-4]。盲卷积技术可以只利用退化图像本身恢复出清晰的目标图像，对于湍流图像复原的研究有很重要的价值，但该方法处理图像时可利用的信息有限[5-6]。后来，Tsumuraya[7]等通过在迭代中使用Richardson-Lucy算法来进行改进，R-L算法根据贝叶斯定理推导出了泊松图像数据的最大似然估计，可以在存在噪声的情况下得到较清晰的复原图像，但存在噪声放大的问题。Llacer[8]在1990年提出了天文图像复原的最大似然估计迭代算法。随后，Synder等研究了CCD相机采样的大气湍流图像基于ML原理的解卷积算法[9-10]，ML算法能够有效去除含有Gaussian和Poisson混合噪声的湍流图像模糊现象。

文中进一步研究并改进了大气湍流退化图像复原算法，利用Zernike多项式进行波前复原，并以此作为点扩散函数(Point Spread Function， PSF)的初始参数估计，以提高算法的复原效果和收敛速度，结合先验信息建立参数估计模型，根据改进的ML算法，建立湍流退化图像代价函数模型。对模拟的湍流退化图像进行复原实验，验证文中算法的有效性。

1 基于波前恢复的大气湍流图像复原

AO系统的工作原理关键在于补偿波前畸变，使目标图像接近衍射极限，从而提高观测图像的质量。成像补偿AO系统的工作原理如图1所示。

图1 成像补偿AO系统工作原理图

畸变光波进入AO系统后，分光镜会将此光波分成两部分：一部分用来成像；另一部分传给波前探测器实时计算成像位移，并将波前形状传给波前控制器，由波前控制器处理波前误差信息，产生误差控制信号，控制波前校正器实时快速改变形状，校正波前畸变。

1.1 湍流图像波前复原

Noll提出，大气湍流造成的任一波前相差均可由一组Zernike多项式表示。口径为D的自适应光学观测系统，湍流相位扰动的波前W(x,y)的Zernike多项式展开式可表示为：

式中：n----Zernike多项式项数；

ck----第k项Zernike多项式对应的模式系数，是均值为零的高斯随机变量；

Zk(x,y)----第k模式项对应的Zernike多项式；

εH----波前相位的复原误差。

CCD探测器的每个子孔径在点(x,y)处测得的波前斜率值可由波前对该点x，y方向求导数得到，其公式可表示为：

式中：εx，εy----分别为x，y方向的波前测量误差。

使用前n项Zernike多项式对有m个子孔径的哈特曼-夏克波前传感器的波前畸变进行整合，当εH足够小时，可得到Zernike波前复原模型为：

式中：G----2m阶波前斜率向量；

D----2m×n阶Zernike多项式复原矩阵；

C----待确定的n阶子孔径多项式系数向量。

波前复原即解线性方程组。式(3)波前复原模型为超定方程(2m>n)，采用奇异值分解法求出波前复原矩阵D的广义逆矩阵D+，则模式向量C为：

最后，由式(1)和式(7)得到完整的波前相位展开式，实现大气湍流退化图像的波前复原。

1.2 基于波前相位的PSF初值估计

PSF初值的选取对于大气湍流退化图像复原算法的效果至关重要[11]，文中利用波前复原的先验信息，估计PSF的初值，以提高初始参数的准确度，加快算法的收敛速度。假设湍流退化图像的降质模型为：

g(x,y)=f(x,y)⊗

式中：g(x,y)----实际观测到的降质图像；

f(x,y)----原始理想图像；

h(x,y)----点扩散函数PSF；

n(x,y)----混合噪声。

用Zernike多项式表示波前畸变量W(x,y)的测量值W0(x,y)：

根据W0(x,y)计算出成像系统的广义瞳函数：

λ----波长。

对系统的广义瞳函数做快速傅里叶变换，得到PSF的初始估计值：

(11)

1.3 改进的ML算法

若目标图像为{f(x)}，PSF为{h(y|x)}，则基于Gaussian模型的极大似然函数可定义为[12]：

式中：γ----调节参数；

θt----波前相位误差；

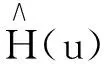
则改进的极大似然函数表达式为：

定义大气湍流退化图像复原的代价函数为：

对式(13)取对数，得到改进的对数极大似然函数表达式：

高清晰湍流退化图像复原就是计算ln(p(g(y)|f,h,a))达到最大时所对应的目标图像f和点扩散函数h，即ln(p(g(y)|f,h,a))分别对f(x)和h(x)求导,并令其导数等于零：

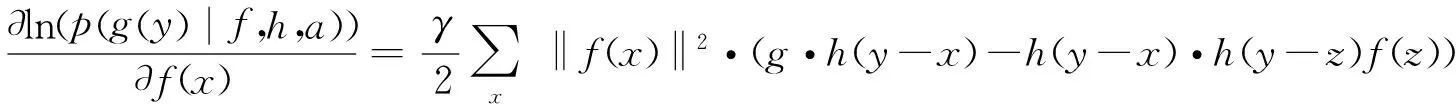
由PSF先验信息可知,∑∑h(y-x)=1，因此可得如下迭代关系式：

式中:β----常数。

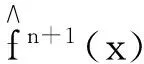
2 仿真实验结果及分析

为充分验证算法的有效性，文中对3幅图像进行了复原实验，在仿真实验中，关键在于对大气湍流效应的去除。实验所用的3幅原始图像如图2所示。

图2 原始图像

图像大小如下:

mountain：512×384像素；

star：256×256像素；

nebulae：599×599像素。

模拟大气湍流对3幅目标图像的影响效果，根据云南天文台1.2m自适应光学系统性能指标设置仿真光学系统的主要参数为：望远镜光瞳直径D=1.02m，成像焦距d=20.12m，成像波长λ=716nm，CCD采样阵列像素大小为7.1μm，大气相干长度r0=17cm。

模拟的湍流退化图像如图3所示。

图3 模拟的大气湍流退化图像

将模拟的湍流图像加入均值为0，标准差为10的高斯白噪声，利用文中算法对模拟的含噪大气湍流退化图像进行复原实验。

图4 3种算法的复原结果图

文中采用无参照图像质量客观评价，用灰度平均梯度(GrayMeanGradient,GMG)来衡量3种算法的复原效果。GMG值越大，表明图像纹理越清晰，复原效果越好。GMG的计算公式为：

表1 不同算法复原后图像的GMG数据

表2 湍流图像与文中算法复原图像的GMG数据

实验结果表明，文中采用的复原算法对大气湍流退化图像的复原效果优于Lucy-Richardson算法和盲卷积算法，可明显提高复原图像的GMG值，能更好地保护图像边缘轮廓及纹理细节。

3 结 语

通过对大气湍流退化图像复原算法的研究，在波前复原的基础上估计PSF初值，引入目标边缘保持约束和PSF约束改进ML算法。通过仿真实验可知，文中复原算法可以有效复原模拟的大气湍流退化图像，得到清晰的目标图像，且目标图像GMG值有明显提高，因此，文中研究结果对湍流图像复原有一定的价值。

[1] 陈善球,刘文劲,董理治,等.闭环控制自适应光学系统变形镜约束技术的研究[J].光学学报,2015,35:15-23.

[2] G A Ayers, J C Dainty. Iterative blind deconvolution method and its applications [J]. Optics Letter,1988,13:547-549.

[3] 温昌礼,徐蓉,门涛,等.基于大气相干长度的湍流模糊图像复原[J].光学学报,2014,34:14-21.

[4] F Sroubek, P Milanfar. Robust multichannel blind deconvolution via fast alternating minimization [J]. IEEE Transaction on Image Processing,2012,21:1687-1700.

[5] 余玉华,董文德,徐之海,等.基于哈特曼-夏克波前传感器的模糊图像复原方法[J].光学学报,2012,32:270-276.

[6] 邵慧,汪建业,王亮,等.基于循环迭代的多帧湍流退化图像复原算法[J].激光与光电子学进展,2014(7):45-52.

[7] F Tsumuraya, N Miura, N baba. Iterative blind deconvolution method using Lucy’s algorithm[J]. Astron Astrophys J.,1994,282:699-708.

[8] 耿则勋,魏小峰,沈忱.结合参数估计的天文图像极大似然恢复[J].光学精密工程,2013,11:2943-2950.

[9] Niu Yiming, Cui Can, Yang Guo, et al. Super-resolution algorithm for passive millimeter wave imaging based on maximum likelihood and neighbor wavelet transform [J]. Sensors & Transducers,2013,157:229-233.

[10] 姜南,李威,黄宗福,等.引入泽尼克多项式的极大似然盲解卷积算法初值的优化选取[J].光学与光电技术,2014,12:25-29.

[11] Rafael Molina, Jorge Nunez, Javier Mateos. Image restoration in astronomy-a bayesian perspective [J]. IEEE Trans. Signal Processing Magazine,2001(3):11-30.

[12] 王宏志，戴娇月，霍金明.基于高阶统计量含噪模糊图像的复原方法[J].长春工业大学学报：自然科学版，2006，27(1):1-3.

Atmospheric turbulence image restoration based on improved maximum likelihood estimation

ZHANG Lijuan1, QIU Huan1, YIN Tingting1, LIU Ying2

(1.School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012， China;2.School of Management Science and Information Engineering, Jilin University of Finance and Economics, Changchun 130117, China)

Zernike polynomial is applied for wavefront reconstruction which is taken as the initial value of the point spread function. With the prior information of images and the improved maximum likelihood estimation, experiment is carried for simulation of turbulence degraded images restoration. The results indicate that image gray mean gradient is obvious improved compared with that of Lucy-Richardson and blind deconvolution algorithm.

turbulence; adaptive optical; wavefront reconstruction; point spread function; maximum likelihood estimation.

10.15923/j.cnki.cn22-1382/t.2017.1.06

2016-12-25

国家自然科学基金资助项目(61402193)； 吉林省社会科学基金资助项目(2015BS48)； 吉林省高校重点实验室基金资助项目( 201401)； 吉林省教育厅“十二五”科学技术研究基金资助项目(2015410)

张丽娟(1978-)，女，汉族，吉林梅河口人，长春工业大学副教授，博士，主要从事计算机视觉及图像处理方向研究,E-mail:zhanglijuan@ccut.edu.cn.

TP 391

A

1674-1374(2017)01-0031-07