基于混合改变惯性因子PSO-BP的短期电力负荷预测
2017-03-31杜晓彬胡土雄
王 伟,杨 跞,杜晓彬,胡 弼,胡土雄
(广东工业大学自动化学院,广东 广州 510006)
负荷预测作为电力系统中的一项非常重要的基础性工作,已成为实现电力系统管理现代化的重要举措之一[1]。其中短期负荷预测主要是指预报未来几小时、1天至几天的电力负荷,对于发电计划、成本、定价上网、电能量交易合同、运行和调度方式等的确定有着重要作用。提高电力系统短期负荷预测的精度不仅能够增强电力系统运行的安全性,还可以改善系统运行的经济性。同时,随着电力市场的进入与开放,其预测精确性与电力市场运营的高效性、企业主体的经营效益密切相关,但是,随着经济体量的不断增大和绿色发展理念的提出,短期负荷预测的问题越来越复杂,现有方法不足以适应多元化因素的叠加,因此有必要做深入的研究,构造最合适的预测方法[2]。
1 研究现状及需要解决的问题
目前,对于短期负荷预测的方法,主要可以分为以下三类:经典预测法、传统预测法、现代预测法[3-7]。经典预测法的优点是计算原理和结构形式简单,存在的不足是预测精度低、无法描述比较复杂的问题、模型初始化难度较大,在实际应用中主要依赖于值班人员的相关经验,采用该方法对预测结果进行验证;传统预测法在传统经验的基础上又增加了数学思想的指导,方法简单、运算方便,但是该类方法主要针对特定情况,无法应用于多种情况;人工神经网络是现代预测法中比较热门的预测方法,同时也逐渐取代了前两种方法,其优点是能够对大量非结构性、非精确性规律进行自主学习、知识推理、优化计算和各种智能处理,尤其是自学习能力和自适应功能是其他算法无法比拟的,其中运用和研究最多的预测模型是BP以及MPSO-BP,但是采用BP和MPSO-BP对电力负荷进行短期预测会出现以下几个问题:
(1)BP、MPSO-BP算法易产生振荡缺陷,预测值与实际值误差大,预测精度不高,误差波动较大,很容易出现过大或过小值,一般最大绝对值误差为20%以上。
(2)BP、MPSO-BP算法各项误差过大,不能很好地优化BP泛化能力和PSO整体搜索能力,依然存在易陷入局部极小值问题,对解不能较好地持续优化跳出局部最优解,对固有缺陷没有明显的改善。
(3)BP、MPSO-BP算法学习速度慢,网络收敛能力不够,BP一般耗时120 s以上,MPSO-BP一般耗时90 s以上。
基于上述问题,同时为了实现能源供需信息的实时匹配和智能化响应,形成“人工智能+电力系统”的新模式,本文采取群体智能与人工神经网络的优化混合预测模型,提出一种随着缺陷变化而跟踪变化的预测方法,即混合改变惯性因子的PSO-BP神经网络算法(PDPSO-BP)。
2 解决方案
负荷预测的核心问题是预测的技术方法,或者说是预测数学模型[8],基于负荷预测方法研究现状的介绍,本文采取最优、最合理数学模型,主体结构以PSO-BP神经网络为主要支撑;同时为了弱化如传统方法出现固有缺陷而造成处理问题单一化、预测精度低等问题的影响,通过对BP、PSO进行理论分析,保留优势性能,针对不足问题构造具有缺陷属性的数学公式,即采用周期改变惯性因子(periodically changing weight,PCW)和动态改变惯性因子(dynamically changing weight,DCW)的双策略,并对传统的流程又增加了额外BP局部寻优,编制了基于MATLAB的混合改变惯性因子PSO-BP神经网络算法(PDPSO-BP)。该方法不仅保留了BP、PSO的优点,又可以较好地提高预测精度,降低预测误差[9-11]。
2.1 负荷预测模型的理论分析
本文通过理论分析BP神经网络算法(back propagation,BP)、粒子群优化算法(particle swarm optimization,PSO)本身固有的优势与不足,针对各自内在缺陷,构造公式并衍化出具有缺陷本质特点,可以跟踪固有缺陷变化而变化,同时保留优势性能的PDPSO-BP算法。
2.1.1BP算法
BP神经网络具有高度的并行性、非线性全局作用、良好的容错性与联想记忆功能以及强大的自适应、自学习功能[12-13]。BP网络可以根据训练样本集给出的已知输出与实际输出之间的差值(误差信号)来调节系统各参数值。BP网络的学习目的是对网络的连接权值进行调整,使得调整后的网络对任一输入都能得到所期望的输出。本文采用3层BP网络结构,结构简洁,减小误差,充分发挥BP网络的优势。
但是BP神经网络也存在一些不足:易产生振荡缺陷;BP算法同时极易陷入局部极小值;学习速度慢。本文根据BP振荡缺陷构造了具有周期性变化的PCW公式。采用具有振荡特性的PCW和动态变化的DCW策略,使权值和阈值处于周期性、动态性的变化过程,从而跳出局部最小值,加快网络收敛速度。
2.1.2PSO算法
PSO算法可以很好地嵌入BP算法,实现从输入到输出的任意非线性映射,同时利用内部交互作用实现由局部最优达到全局最优。
PSO算法具有较快的逼近最优解的速度,可以有效地对系统参数进行优化,它的本质是利用当前位置、局部最优值和全局最优值三个信息,指导粒子下一步迭代动向,但是PSO算法的最主要问题是易产生早熟收敛、易发散、局部寻优能力较差,同时其易陷入局部最小。本文根据PSO算法本质及易发散的缺陷,使用含有上述三个有效信息的DCW公式,使得惯性因子w动态变化,防止早熟,跳出局部最小,提高全局寻优能力。
2.2 PDPSO-BP神经网络
2.2.1PDPSO-BP算法理论
通过对BP、PSO算法的理论分析,本文保留原有的优势特点,如BP网络结构,PSO速度、位置更新公式等,构造具有缺陷属性的惯性因子,扩展算法流程,增加BP局部寻优。虽然PSO-BP算法[14-18]相对单一BP算法收敛速度快、精度高,不受模型结构的影响,但是,PSO与BP算法本身固有的缺陷依然存在:首先,针对BP算法的易振荡、PSO算法的易发散,本文采用周期性改变惯性因子PCW,的方法,如公式(2),余弦函数本身具有周期性变化的特点,其周期振荡特性可以很好地符合与适应BP易振荡、PSO易发散的固有缺陷,通过余弦函数的周期变化快速适应位置并确定w的大小;其次,对于PSO算法不能对解进行持续优化,而是在局部最优解附近徘徊的缺点,更改优化策略采用动态性改变惯性因子DCW的方法,在公式(3)中,进化度e考虑到了粒子以前的运行状况,反映了粒子群在速度上进化的程度,同时聚合度a反映了当前的粒子群的聚散性,两个动态变量使得粒子处于动态更新状态,所以可以动态改变w的大小,从而在对解进行持续优化的过程中,可以修正在局部最优解附近徘徊的缺陷,因此可以达到改善BP的泛化能力,从整体上提高PSO的搜索能力,动态更新粒子的速度和位置,加快网络收敛速度的效果;最后,针对PSO算法后期局部寻优能力差的缺点,本文又额外采用把PSO算法反复优化的参数(权值、阈值)赋予BP网络进行再次局部寻优的方法,以达到提高预测精度,降低预测误差的目的。
2.2.2速度、位置更新公式
PDPSO-BP算法依据PCW和DCW公式更新惯性因子w,优化局部和全局最优值,并以周期性、动态性原则更新粒子速度和位置。根据shi等人提出的标准PSO算法,粒子的速度和位置更新公式如下:
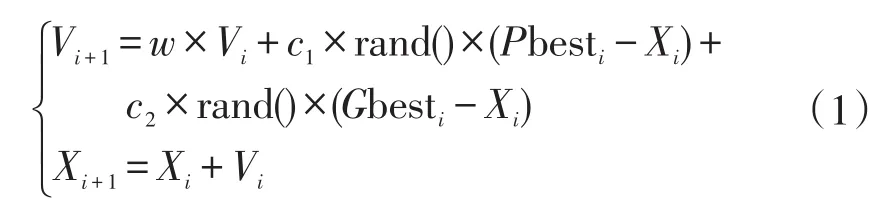
式中:Vi—粒子的速度;
Xi—粒子的当前位置;
Pbesti—目前为止局部最优值;
Gbesti—目前为止全局最优值;
rand()—介于(0、1)之间的随机数;
c1和c2—学习因子;i=1,2,…,N。
2.2.3混合惯性因子公式
(1)PCW公式
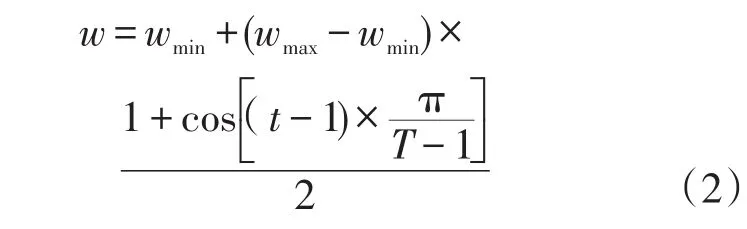
式中:t—迭代次数;
T—最大迭代次数;
wmax、wmin—分别为初始惯性因子最大、最小值。
根据公式(2),随着迭代次数的递增,w呈现余弦性周期变化,以周期振荡特性适应BP易振荡、PSO易发散的缺陷快速找到位置并确定其大小。
(2)DCW公式
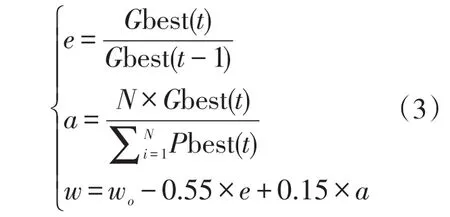
式中:wo—初始惯性因子;
e—粒子进化度;
a—粒子聚合度;
Gbest(t)、Gbest(t-1)—分别指当前和前一次的全局最优值;
N—粒子总数;
Pbest(t)—局部最优值。
参数e考虑到了粒子以前的运行状况,反映了粒子群在速度上进化的程度。参数a反映了当前的粒子群的聚散性[19]。PDPSO-BP混合算法在粒子更新过程中根据e和a的值动态改变w,从而优化了算法的性能。
2.2.4PDPSO-BP算法实现过程及流程图
根据PCW、DCW公式优化惯性因子,形成基于混合惯性因子的PSO-BP算法,即PDPSO-BP算法,其步骤如下:
Step1,初始化粒子群参数;
Step2,根据训练样本集确定神经网络的拓扑结构;
Step3,计算每个粒子的适应度值;
Step4,比较适应度值,确定每个粒子的局部最优值Pbest和全局最优值Gbest;
Step5,检验是否达到终止条件,如果是,达到最大迭代次数或者预定误差,则停止迭代,输出最终权值和阈值赋给BP进行局部寻优,完成负荷预测,否则,执行Step6;
Step6,根据式(2),PCW方法计算惯性因子w(当迭代次数t>1时,根据式(3)DCW方法计算惯性因子w),再根据式(1)更新粒子速度和位置,迭代加1,返回至Step3。
程序流程如图1所示。
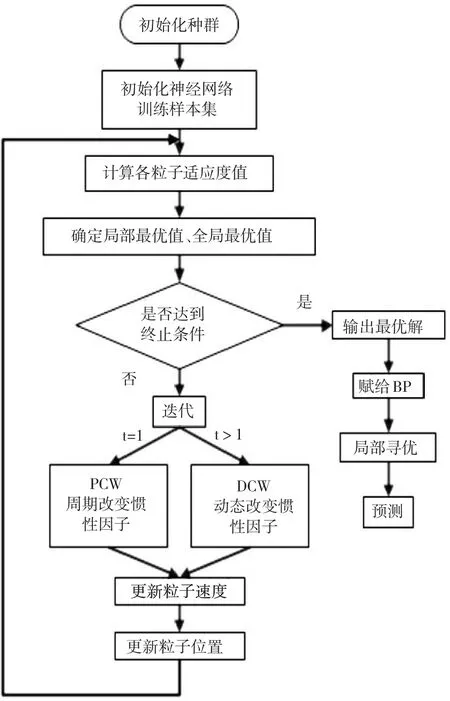
图1 PDPSO-BP算法流程
3 负荷预测模型建立与仿真分析
3.1 样本集的选择
本文选择广东某城市5月1日到7月30日的负荷值以及5月2日到7月31日的气象特征状态作为网络的训练样本,通过该训练样本来预测7月31日的电力负荷。
3.2 学习样本的分析与处理
(1)原始数据的垂直处理。数据垂直处理适用于不同日期的同一时刻的负荷具有相似性,且维持在一定的范围内,广东5、6、7月份气温变化均匀,处于夏季负荷消耗状态,因此本文采用垂直处理的方法,负荷数据预处理时考虑其24 h的小周期,同时还要考虑天气因素和特别事件因素对数据的影响,对于超出范围的不良数据修正,其修正值为待处理数据的最近几天该时刻的负荷平均值。
(2)负荷数据取样。本文采取24小时制,并规定第1个时间点为当天凌晨两点,第2个时间点为当天凌晨四点,剩余时间点按此顺序依此类推,则第12个时间点为当天二十四点,即隔天零点。在预测日的前一天中,每隔2 h对电力负荷进行1次测量,这样1天可以得到12组负荷数据,将前一天的实时负荷数据作为网络的样本数据。
(3)天气因素量化。另外电力负荷还与环境因素有关,所以本文还考虑了气温大小和天气特征。即最高、最低气温和天气特征,可以通过天气预报得到预测日的最高、最低气温和天气特征,用0、0.5、1分别表示晴天、阴天、雨天,将预测当天的气象特征作为网络的输入变量,这样输入变量P就是一个15维的向量,即n=15;目标向量就是预测日当天的12个负荷值,即输出变量T为一个12维的向量,m=12。
隐含层个数的确定。根据经验公式:
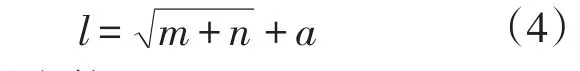
式中:m—输出变量个数;
n—输入变量个数;
a —1~10之间的整数[20]。
经过多次试验,隐含层的最优取值为10。
(5)归一化处理。由于在输入的数据中各类型的数据大小、单位都不统一,这样大大增加了系统的运算量、运算时间还降低了精度甚至可能使神经元趋于饱和不能继续运算。为了避免神经元的饱和性,在确定输入和输出变量后,应对其进行归一化处理,将数据处理为一定范围之间。这样就降低了运算量,提高运算速度和时间。
(6)确定网络拓扑结构。本文在选择网络结构的过程中,对不同的网络结构,都通过试验参数,采用PDPSO-BP算法优化,从中优选得到误差较小的15-10-12最佳网络结构。如图2所示。
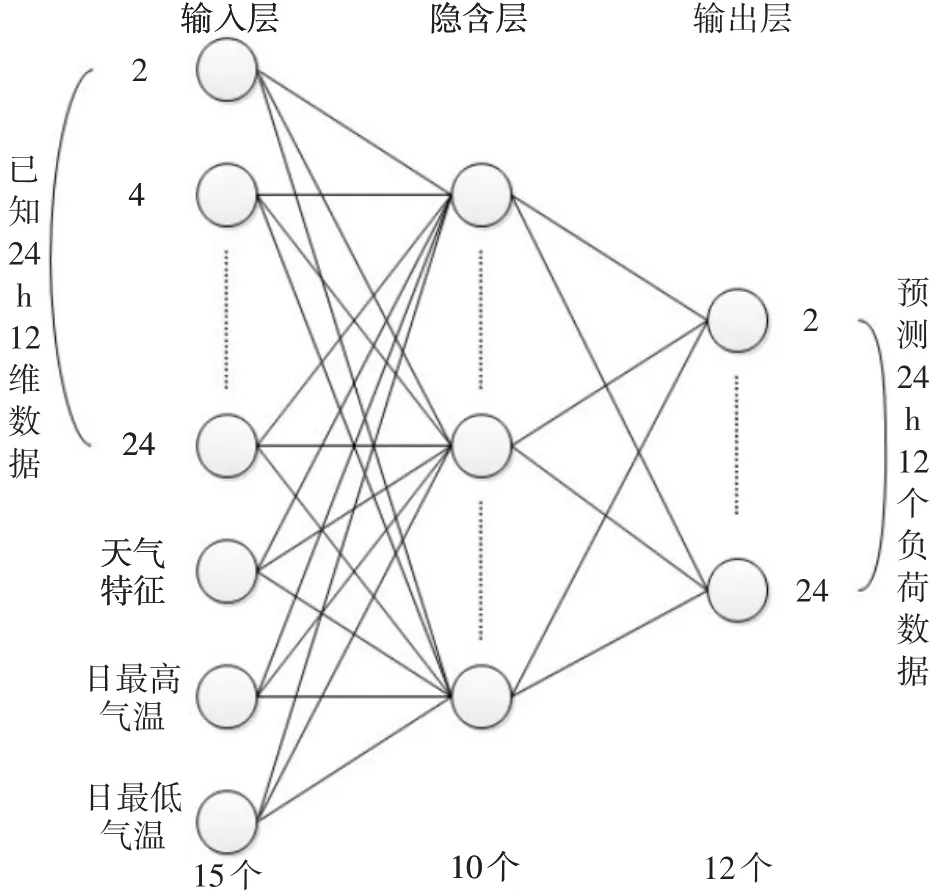
图2 PDPSO-BP网络拓扑结构
3.3 仿真与分析
本文PDPSO-BP神经网络中的参数设置:wmax=1.2,wmin=0.6,wo=0.9,种群 N=30,优化变量个数D=292,学习因子c1=c2=2.5,PSO迭代次数 T=300,rand()∈(0,1);BP网络结构15-10-12,迭代epoch=100,精度goal=0.01,学习速率lr=0.05。使用MATLAB软件在相同精度控制条件下,分别对传统的BP神经网络、MPSO-BP神经网络和PDPSO-BP神经网络进行仿真比较。
从表1可以看出,PDPSO-BP神经网络负荷预测误差绝对值在0%~3%之间变化,波动平缓。其他两种神经网络预测波动过大,存在较大误差,在第2个时间点出现了大幅度变化,影响预测的准确性。
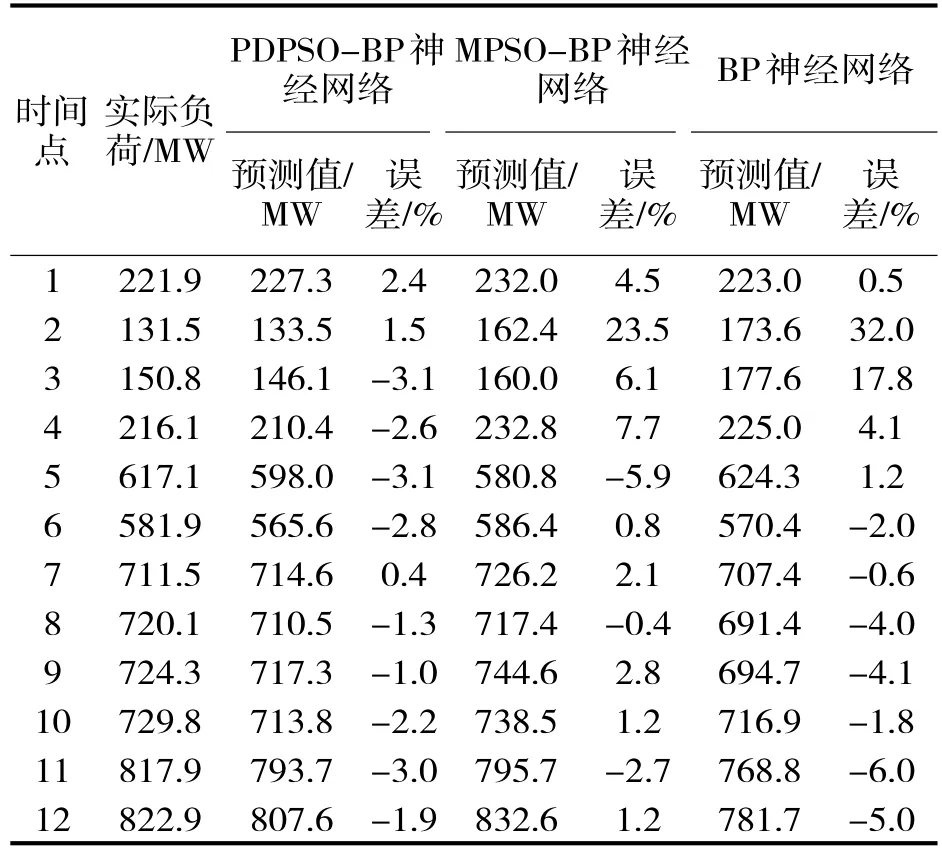
表1 负荷预测误差
从表2可以看出,本文构建的PDPSO-BP负荷模型,平均绝对误差(mean absolute error,MAE)为1.07%,均方根误差(root-mean-square error,RMSE)为1.27%,和方差(sum of squares for error,SSE)为1.95%,最大相对误差为3.14%,精度较高,达到了短期负荷的误差要求,而BP神经网络、MPSO-BP神经网络最大相对误差过大,不满足负荷的要求。
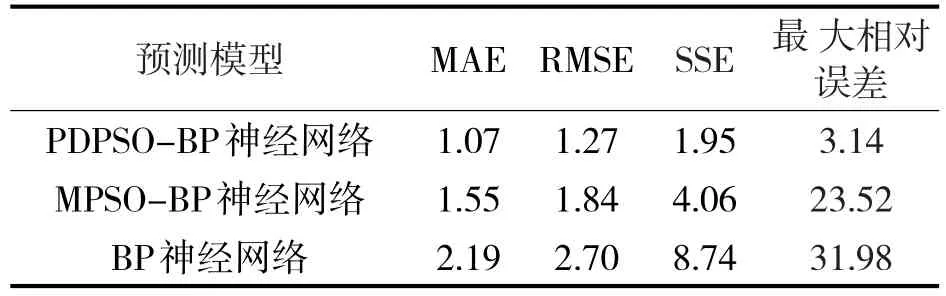
表2 预测模型误差比较%
从表3中可以看出,在相同控制精度下,PDP-SO-BP算法比BP、MPSO-BP算法的网络收敛速度更快,有效地处理了学习速度慢的问题,所以,PDPSO-BP算法较其他两种算法更适于快速寻找权值和阈值进行负荷预测。
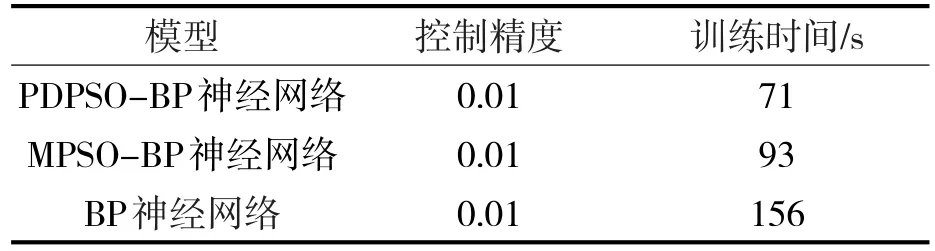
表3 预测时间比较
从表1、表2和表3中可以看出,本文构建的PDPSO-BP神经网络在预测误差、MAE、RMSE、SSE和最大相对误差各方面都明显优于BP神经网络、MPSO-BP神经网络,预测精度高,网络收敛速度快,适用于短期负荷预测。
通过MATLAB构建误差函数,对三种负荷预测误差分点采样,如图3所示,可以看出PDPSOBP算法的百分误差变化比较均匀,在0%~3%之间变动。而BP神经网络、MPSO-BP神经网络在第2个时间点出现较大偏差,影响整体负荷预测。
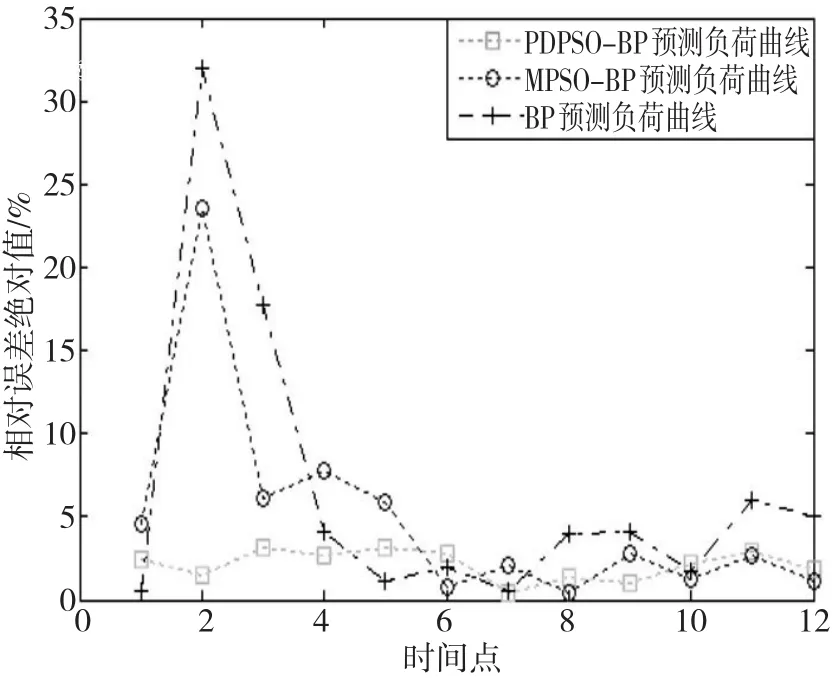
图3 负荷预测的百分误差
从图4可以看出,PDPSO-BP负荷预测曲线与实际负荷曲线更加吻合,本文所设计的PDPSOBP神经网络的负荷预测精度要高于传统的BP神经网络和MPSO-BP神经网络。
如表1-表3和图4-图5所示,PDPSO-BP神经网络模型与传统的BP神经网络和MPSO-BP神经网络相比,降低了预测误差,提高了预测精度,耗时较短。所以,采用PDPSO-BP算法对于短期负荷预测具有更高的准确度以及更好的收敛性。
4 效果评价
(1)由表1负荷预测误差和图3百分误差绝对值对比中可以得出,PDPSO-BP神经网络预测值与实际值误差绝对值最大为3.1%,最小为0.4%,整体误差波动小,变化均匀,误差绝对值范围控制在0%~3%之间,没有出现过大或过小值。而BP神经网络误差绝对值最大为32%,最小为0.5%;MPSO-BP神经网络误差绝对值最大为23.5%,最小为0.4%。PDPSO-BP有效地克服了BP预测精度低的问题,提高了网络泛化能力和预测精度。
(2)在表2中可以看出,PDPSO-BP神经网络MAE为1.07%,比BP小一倍,比MPSO-BP小30%;RMSE为1.27%,比BP小一倍多,比MPSO-BP小31%;SSE为1.95%,BP是它的4.5倍,MPSO-BP是它的2倍;最大相对误差为3.14%,BP是它的10倍,MPSO-BP是它的7.5倍。PDPSO-BP算法很好地解决了BP振荡性和PSO发散性缺陷,克服了易陷入局部极小值问题,同时对解持续优化跳出局部最优解,比MPSO-BP更加完善。
(3)从表3中可以看出,当精度goal=0.01时,PDPSO-BP算法训练时间为71 s,比BP小一倍,比MPSO-BP小24%,整体耗时短,提高了网络收敛速度。
(4)从图4负荷预测曲线的对比中可以得出,PDPSO-BP算法预测曲线更加贴近实际曲线,具有更高的预测精度,更适用于短期负荷预测。
5 结论
(1)本文提出的PDPSO-BP神经网络预测模型通过构造和引用公式PCW和DCW,采取具有缺陷属性的方法针对固有缺陷周期性、动态性地改变惯性因子,克服BP、PSO振荡性和发散性,对解持续优化跳出局部最优解,克服了易陷入局部极小值问题。
(2)PDPSO-BP神经网络预测模型比BP、PSO耗时更短,效率更高,加快网络收敛速度,提高了预测精度和降低了误差,表现出良好的稳定性,满足短期负荷预测的基本要求。
(3)PDPSO-BP负荷预测方法继承了群体智能与人工神经网络的混合预测模型的优势,摒弃了经典预测法和传统预测法的主体结构,加强并优化了自学习能力和自适应功能,改善BP的泛化能力,提高PSO的整体搜索能力,动态更新粒子的速度和位置,适用于短期电力负荷预测。
[1] 张慧芳.负荷预测管理在新经济形势下的作用[J].合作经济与科技.2015(12):107.
[2] 李芳.负荷预测对电力市场竞争的影响分析[D].郑州:郑州大学,2013.
[3] 康重庆,夏清,张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自动化,2004,28(17):1-11.
[4] 牛东晓,曹树华,卢建昌,等.电力负荷预测技术及其应用[M].北京:中国2版.电力出版社,2009.
[5] 杜雅楠,郭志娟,吕灵芝,等.短期电力系统负荷预测方法综述[J].技术与市场,2015,22(5):339-340.
[6] 廖旎焕,胡智宏,马莹莹,等.电力系统短期负荷预测方法综述[J].电力系统保护与控制,2011,39(1):147-152.
[7] ZHUANG Linlin,LIU Hai,ZHU Jimin ,et al.Comparison of forecasting methods for power system short-term load forecasting based on neural networks[C].//2016 IEEE International Conference on Information and Automation(ICIA).IEEE Conference Publications,2016,114-119.
[8] 黄海涛,魏明磊,谢海波,等.基于改进纵横交叉算法的多目标无功优化[J].宁夏电力,2016,(6):19-26.
[9] 樊振宇.BP神经网络模型与学习算法[J].软件导刊,2011,10(7):66-68.
[10] 张丽丽.PSO算法介绍[J].山西财经大学学报,2007,29(2):214-215.
[11] KENNEDY J,EBERHART R.Particle swarm optimization[C].Proceedings of the IEEE International Conference on Neural Networks.IEEE Conference Publications,1995,1942-1948.
[12] 黄欣,赵锦成,解璞.基于BP神经网络的电站负荷预测仿真研究[J].研究与开发,2012,31(10):41-43.
[13] 周英,尹邦德,任玲,等.基于BP神经网络的电网短期负荷预测模型研究[J].电测与仪表,2011,48(542):68-71.
[14] 张永革,石季英,张文,等.复杂遮阴条件下光伏系统MPPT控制改进PSO算法仿真研究[J].中国电机工程学报,2016,34,39-46.
[15] 乔维德.基于改进PSO-BP神经网络的短期电力负荷预测研究[J].继电器,2007,35(17):17-21.
[16] 田丽,夏新运,蒋慧,等.基于PSO-BP混合算法的短期电力负荷预测[J].自动化与仪器仪表,2009,(2):40-53.
[17] 师彪,李郁侠,于新花,等.改进粒子群-BP神经网络模型的短期电力负荷预测[J].计算机应用,2009,29(4):1036-1039.
[18] DOMMEL HW,Tinney.WF.Opti mal power flower solutions[J].IEEE Transactions on Power Apparatus and Systems 1968,87(1):1866-1876.
[19] 朱小六,熊伟丽,徐保国.基于动态惯性因子的PSO算法的研究[J].计算机仿真,2007,24(5):154-157.
[20] 张少迪.基于PSO-BP神经网络的短期负荷预测算法[J].现代电子技术,2013,36(12):155-162.
