基于NSGA2算法的成像卫星星座多目标任务规划问题研究
2017-03-31黄瀚张晓倩
黄瀚+张晓倩

摘 要:微小卫星构成的星座在气象、军事等领域发展极为迅速。针对成像卫星星座多目标任务规划问题,以成像目标等级、资源消耗和成像效果为目标函数,建立了成像卫星星座任务规划的问题模型。将非劣排序遗传算法2 (NSGA2) 应用于求解成像任务规划问题中,通过MATLAB仿真验证了NSGA2 算法求解多目标成像问题的可行性和有效性。
关键词关键词:成像卫星星座;任务规划;MATLAB仿真;NSGA2算法
DOIDOI:10.11907/rjdk.161621
中图分类号:TP319
文献标识码:A 文章编号:1672-7800(2016)008-0143-04
0 引言
成像卫星的作用是利用携带的各类遥感器对地表成像并将获得的数据传输到地面站[1]。成像卫星在气象预报、环境保护和军事侦察等领域都有著极为重要的作用[2]。
本文的主要研究对象是具有星间通信能力的成像卫星星座。该成像卫星星座由两颗星组成,这两颗星均运行在轨道高度为600km的太阳同步轨道上。其中一颗星携带有可见光遥感器,有单景模式和条带模式两种成像方式;另一颗星作为通信星且未携带成像载荷,可与成像星进行数据传输,以缩短数据回传时间。这种成像卫星星座模型是本文的立足点,文中所有研究都是基于该成像卫星星座模型。
1 成像卫星星座任务规划问题描述及建模
1.1 成像卫星星座任务规划问题描述
成像卫星星座任务规划问题是一个多目标的优化问题,需要考虑任务重要性、资源消耗、数据时效性、成像效果等。本文选择了3个具有代表性的目标(任务重要性、资源消耗、成像效果),对成像卫星星座任务规划问题模型进行多目标任务规划。在任务设计中,多目标优化算法选择了后验式的NSGA2算法,该算法比较适用于成像卫星星座任务规划问题[3]。
1.2 成像卫星星座任务规划的数学规划模型
具有星间通信能力的成像卫星星座任务规划与传统多星任务规划有所不同,各任务之间的耦合性更强。不仅需要考虑成像任务之间的冲突,还需要考虑数传任务之间以及两种任务之间的冲突。
成像星在其固定轨道上飞行,当其遥感器的覆盖范围出现了成像目标,就可能执行成像任务,当满足与地面站的通信条件,则可能执行数传任务。而当通信星的飞行轨道与成像星的轨道在极地区会合时,满足星间数传条件则可能执行星间数传任务。
设计星座中两颗星的轨道高度为600km,轨道类型为太阳同步轨道。通信星与成像星的星间数传距离约为200~300km,相应的星间相对相位约为1.7°~2.5°。
星间相对相位关系的计算公式为:
α=2arcsin(d/h)(1)
其中,α表示星间相对相位(°);d为星间相对距离(m);h为轨道高度(m)。在STK环境下,假设有4个地面站分别是北京、喀什、海口和哈尔滨,其经纬度如表1。
成像星携带的成像载荷为Simple Conic,坐标系统为J2000,仿真开始时间为1 Jul 2007 12∶00∶00.000,结束时间为3 Jul 2007 12∶00∶00.000,仿真步长为60sec。根据这48hours的仿真,可以得到每个采样时刻成像星和通信星在惯性坐标系下的位置信息和星下点轨迹信息,将该信息导入MATLAB中构成双星轨迹模型。仿真的三维效果如图1所示。
根据该STK模型的数据和对其任务规划过程的分析,可以建立其数学规划模型。
1.2.1 约束条件建模
(1)成像任务时间窗口约束为d(imagePositioni、imagePositionj)<6。约束中imagePositioni表示成像任务目标的地理位置;d表示距离函数,在经纬度坐标下,计算两个任务目标之间的经纬度距离,当距离小于6时,由于卫星的飞行速度和成像开关机所需时间等原因,导致两个任务不能同时执行,只能任选其一。
(2)各地面站与卫星的通信仰角约束为αij>5。其中αij是指第i个卫星与第j个地面站的通信仰角。一般来说,当卫星与地面站之间的通信仰角小于5°时,卫星与地面站就不能进行数据传输。
(3)通信星与成像星的通信距离约束为d(Track_Sai、Track_Sbi)<300km。其中,Track_Sai表示成像星在i时刻的经纬度坐标;Track_Sbj表示通信星在i时刻的经纬度坐标;当双星距离大于300km,认为不满足通信条件。
(4)可见光遥感器的光照条件约束为Solar_anglei δ=23.45sin2πd365;Solar_angle=arcsin(sinφsinδ+cosφcosδcosω)(2) 式中,d表示某年中某一天的日期序号;φ表示当前成像任务目标的地理纬度;δ表示太阳赤纬;ω表示太阳时角。 (5)成像任务的云量等级约束为Cloudyi 1.2.2 目标评价函数建模 根据卫星星座成像任务规划模型特点设计了3个目标评价函数,分别是成像效果评价函数、资源消耗评价函数、任务重要性评价函数。 (1)成像效果评价函数的计算公式为: 其中,Solar_angle、Cloudy分别表示成像任务所在位置的太阳高度角和云量等级;w_a、w_c分别表示太阳高度角下限和云量等级上限[4];w1、w2用来统一量纲,无实际意义。
(2)资源消耗评价函数的计算公式为:
式中,imageChange为执行成像任务所需的侧视角度;za为侧视机动中单位时间内消耗的能量;vl为侧视机动的角速率。
为了保证多目标优化方向的一致性,资源消耗评价值采用了总能量与消耗能量之差。
(3)任务重要性评价函数的计算公式为:
表达式中包括了成像任务的重要性权值和数传任务的重要性权值,dl_qz为数传任务的重要性权值。
2 NSGA2算法分析
2.1 多目标优化概念
多目标优化问题指在给定的解空间中搜索满足至少一个目标评价函数的解的问题。
其数学表达式如下:
式中,x是决策矢量,即为多目标优化问题的解;X为优化问题所有可行解构成的解集合;y是目标矢量,对应于多目标优化问题的一组评价值;Y为所有评价值构成的目标集合。
Pareto最优解是指当对于一个属于解空间的解∈Ω,不存在其它任意解∈Ω,使得相应的目标评价值f( )≥f( ),则认为该解为多目标优化问题的一个Pareto最优解。
2.2 NSGA2算法
NSGA2算法即非支配选择排序遗传算法,是由Deb[5]等提出的一种后验式的多目标进化算法。NSGA2算法的基本思想是在遗传算法的基础上,增加一个非支配选择排序和拥挤度计算的环节。将NSGA2算法应用于成像卫星星座任务规划中时,对其作适当改进,其程序流程如图3所示。在该程序流程中,引入精英解保持策略过程。在形成新父代种群之前,将旧父代和子代合为一体并进行非支配排序和拥挤度计算。运用这种方式,不仅能够保留旧父代中的精英解,而且扩大了个体的采样空间。
3 基于MATLAB的多目标任务规划仿真
仿真中可见光遥感器的参数主要来自quickbird卫星,假定其单景模式成像范围为36.5km×36.5km,NSGA2算法假定所有的成像任务目标均为已分解的点目标任务。实验中设计了14个点目标任务,其参数如表3所示。
在仿真中,假定成像星只有一颗,只携带了一种遥感器即CCD相机,结合成像任务的用户需求,成像任务面临的约束如表4所示。
说明:①表中云量等级指成像星所携带的遥感器对云量等级的要求,云量等级共分为9级,级别越高,气象条件越差,这里给出的是云量等级的上限;②表中太阳高度角是指成像星成像所需的光照条件约束,给出太阳高度角的下限,如果成像目标所在地的太阳高度角小于该下限,认为成像无效;③表中任务权重指成像任务的优先级,共分为9个级别,级别越高,表明该任务优先级越高。
NSGA2算法中种群编码采用的是二进制编码,种群的选择方式采用赌轮盘选择法,交叉方式采用单点交叉法,概率为0.9,变异操作则是采用取反的方法,变异概率为0.1。算法终止条件为运行300代。
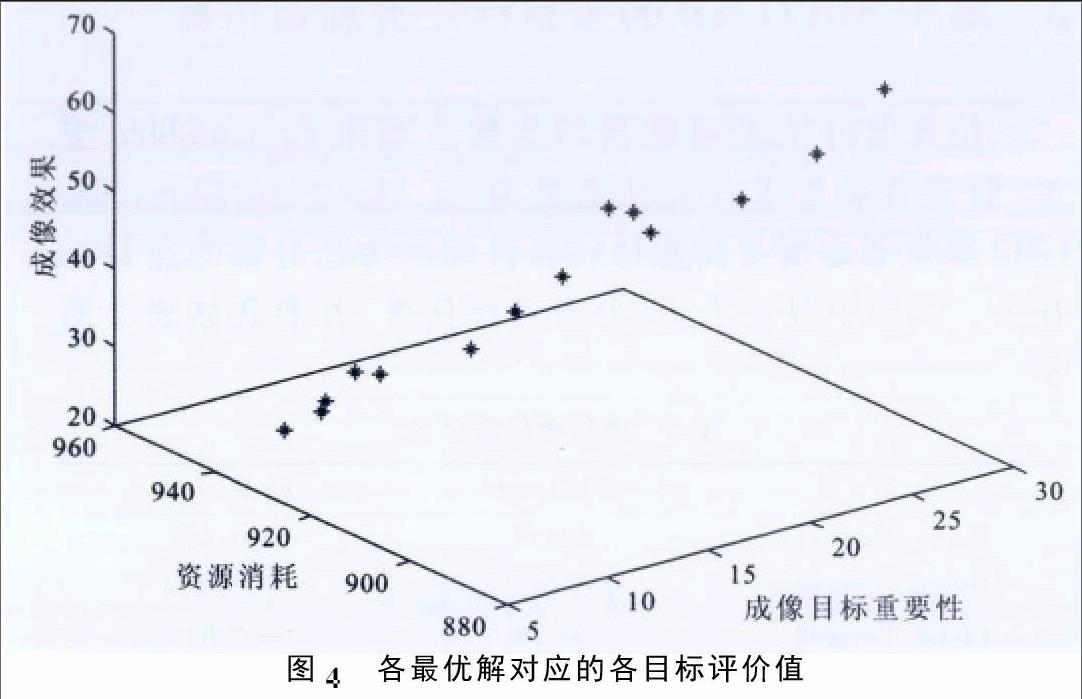
NSGA2算法是基于概率的算法,需运行10次得到其统计意义下的Pareto最优解集。其中各解对应的评价值如图4所示。从图4中各点坐标可以看出,NSGA2算法得到了在3个目标评价值都比较好的解,而淘汰了某些目标评价值很高但其它目标评价值很低的解。在得到这些Pareto解后,需要对其进行决策,即选择其中的一个解作为最终解。
仅分析成像目标重要性和资源消耗这两个目标,如图5所示。
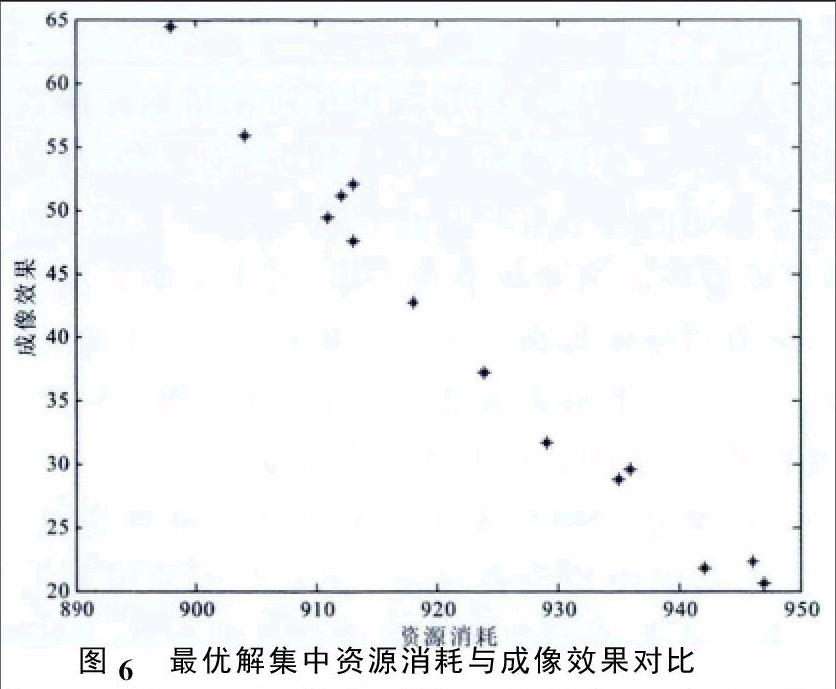
仅分析资源消耗与成像效果目标如图6所示。可以看出得到的最终解集在这两个目标上都有很好的体现,也证明了最终解集中的各解是均为Pareto最优解。
选择当中的一组解作为成像任务的规划方案,成像任务规划结果如表5所示。
由表5可以看出,有4个任务不满足成像约束条件在预处理中被剔除,各目标函数的评价值分别为28、898、64.43。成像重要性评价值的范围大致为5~30,资源消耗评价值的范围大致为880~950,成像效果评价值的范围大致为20~70。由NSGA2算法得到的多目标最优方案较为合理。
4 结语
具有星间数传能力的成像卫星星座可以极大提高数据的时效性,未来成像卫星星座中具有很大发展空间,因而对具有星间数传能力的成像卫星星座的任务规划问题研究具有现实意义。本文分析了能够进行星间数传的成像卫星星座的工作过程,对其任务规划可能面对的约束进行了讨论,建立了成像卫星星座的数学模型,并利用NSGA2算法对该模型进行了求解,取得了不错的效果。本文仅讨论了双星情况下的任务规划,在后续研究中,可以验证多星任务冲突时NSGA2算法的应用效果。
参考文献:
[1] 葛榜军,廖春发.总装备部卫星有效载荷及应用技术专业组应用技术分组[M].北京:中国科学技术出版社,2001.
[2] 张钧屏,方艾里,万志龙.对地观测与对空监视[M].北京:科学出版社,2001.
[3] 蓝艇,刘士荣,顾幸生.基于进化算法的多目标优化方法[J].控制与决策,2006,21(6):601-605.
[4] 王国安,米鸿涛,邓天宏,等.太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学,2007,30(B09):161-164.
[5] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
(責任编辑:孙 娟)
