混沌遗传算法在高校排课系统上的应用

谷雅宁

摘 要 排课问题有很多制约因素，其目的是要找出各因素间的最佳对应关系，因此高校排课问题就是一个非线性组合优化问题。遗传算法是解决非线性组合优化问题的有效智能算法，但是遗传算法可能会陷入局部最优的局面，并且收敛速度比较慢。为了弥补这些缺陷，本文利用混沌的遍历性、随机性、内在规律性和遗传算法的反演性，采用混沌遗传算法来解决高校排课问题。实验结果表明：当运行趋于稳定状态时，该混沌遗传算法比遗传算法收敛速度快、能更有效地求得全局最优解。

关键词 排课 混沌优化 混沌遗传算法

中图分类号：G642 文献标识码：A DOI：10.16400/j.cnki.kjdks.2016.12.007

Abstract There are many constraints in the course of scheduling， the purpose is to find out the best correspondence between the various factors， so the problem is a nonlinear combinatorial optimization problem. Genetic algorithm is an effective intelligent algorithm to solve nonlinear combinatorial optimization problems， but the genetic algorithm may fall into the local optimal situation， and the convergence speed is relatively slow. In order to make up these defects， this paper uses the chaos of the ergodic， random， intrinsic regularity and genetic algorithm inversion， using chaos genetic algorithm to solve the problem of college course arrangement. The experimental results show that the chaotic genetic algorithm can get the global optimal solution faster than the genetic algorithm when the operation is stable.

Keywords course scheduling； chaos optimization； chaos genetic algorithm

美国Michigan大学的John Holland教授最早提出了遗传算法。它是一种解决NP完全问题的有效方法。De Jong首先将其用于函数优化问题的研究中，并验证了GA是一种解决优化问题的有效的算法。Dorigo利用遗传算法对高中课程进行排课，也验证了GA是一种有效的排课算法。但是对于复杂的非线性系统优化问题的求解，GA仍有许多缺陷，如进化过程的过早收敛；无法保证收敛到全局最优解；群体中最好的染色体的丢失等。为了避免出现这些问题，本文把混沌引入到遗传算法中（即混沌遗传算法），利用混沌序列的内在规律性，有效地引导交叉和变异操作。

1 建立数学模型

1.1 模型描述

假设学校有N个班，N={ni|i=1，2，3，…，N}，各个班级人数为{i|=1，2，3，…，N}；班级集合有T个教师，T={t1，t2，…，tT}；课程总数为S，S={s1，s2，…，sS；教室個数为R，R={r1，r2，…，rR}，各教室可容纳人数为{x1，x2，…，xR}；时间段数为M个，M={m1，m2，…，mR}。

1.2 模型中的约束条件

1.2.1 软约束条件

（1）满足教师所提出的上课时间和地点的特殊要求。（2）多学时课程的周安排要错开，一般对于每周多学时的课程应该能够尽量将其隔1天以上安排才能保证有较好的教学效果。（3）在排课过程中较难的课程最大程度地安排在授课效果较好的节次中，比如上午上课效果要比下午效果好。

1.2.2 硬约束条件

（1）同一时间，同一班级不能同时有两门以上的课程。（2）同一时间，同一个教师不能同时有两门以上的课程。（3）同一时间，同一个教室不能同时有两门以上的课程。（4）分配的教室可容纳人数应该大于等于上课的班级的学生人数。

1.3 建立的数学模型

排课问题的数学模型是一个组合优化问题，其中f为目标函数。目标函数值为4时最为理想，从此可看出排课问题是一个求最大值问题。其中R1表示老师对课程有没有特殊要求，若有则R1=1，否则R1=0。R2表示周学时的大小，若周学时大则R2=1，否则R2=0。R3表示课程的级别，若为必修课则R3=1，否则R3=0。R4表示可是课程难度级别，若课程难度大的安排在上午或课程难度小的安排在下午则R4=1，否则R4=0。Ki表示以上的权重，其中由以上各自的优先级可令K1≥K2≥K3≥K4≥0，Ki=1。教师tt在时间mm、教室rr中给班级nn讲授课程ss，表示nnttssrrmm=1，反之为nnttssrrmm=0。

2 混沌遗传算法

混沌遗传算法是在遗传算法的过程中加一混沌扰动，从而提高了收敛速度，找到全局最优解。

2.1 步骤

（1）编码。二进制编码不能很好地反映排课问题的特点，且交叉和变异较难操作。本文采用浮点数编码，因为其自然直观、交叉和变异操作较容易、解码操作也非常容易、节省时空开销、计算效率高。

（2）生成初始群体。混沌遗传算法利用混沌的遍历性进行粗粒度全局搜索获得比随机搜索有更好的效果，从而提高初始种群个体的质量和计算效率。

（3）确定个体适应度函数。确定个体适应度真正目的是确定个体在群体中的优劣。适应度越大个体越好，反之适应度越小则个体越差。根据适应度的大小对个体进行选择，以保证适应性能好的个体有更多的机会繁衍后代，使优良特性得以遗传。因此适应度函数设定的好坏直接影响到混沌遗传算法的收敛速度和能否找到最优解。由于排课问题的软约束条件有多个，因此本文采用多目标化的个体适应度函数。

（4）确定交叉概率Pc，并执行交叉操作。在混沌遗传算法的整个进化过程中交叉操作要进行成千上万次。遗传算法中的交叉算子主要采用单点、对称、大片断基因保留、小片断基因保序的交叉方法。而在混沌遗传算法中， 利用混沌序列来控制交叉操作，从而提高交叉的效率。①混沌序列控制交叉频率：交叉概率在很大程度上影响着算法的收敛速度和解的质量。混沌遗传算法利用混沌序列对目标基因进行混沌扰动，从而加快了算法的收敛速度和解的质量。其中0.25≤Pc≤1.0比较理想。②混沌序列控制交叉点位置的选择：由产生的一个混沌序列映射到该目标个体的基因空间，则在相应的位置进行交叉操作。

（5）确定变异概率Pm，并执行变异操作。在混沌遗传算法中，产生的混沌序列来控制变异算子。从而提高变异的效率。①混沌序列控制变异频率：混沌遗传算法利用混沌序列对目标基因进行混沌扰动，从而提高了解的质量。其中0.001≤Pm≤0.1比较理想。②混沌序列控制变异点位置的选择：由产生的一个混沌序列映射到该目标个体的基因空间，则在相应的位置进行变异操作。

（6）适应度较低个体的混沌优化。混沌遗传算法利用混沌进行细粒度局部搜索，提高解的精度。對当前代群体中适应度较小的90%的基因加混沌扰动。这种变异可能产生比剩下10%较高适应度基因更好的基因，从而有效地避免单纯的遗传算法陷入局部最优解与早熟的问题。

（7）判断该算法收敛准则是否满足终止条件，若满足则输出搜索结果，否则返回（4），直到满足终止条件。

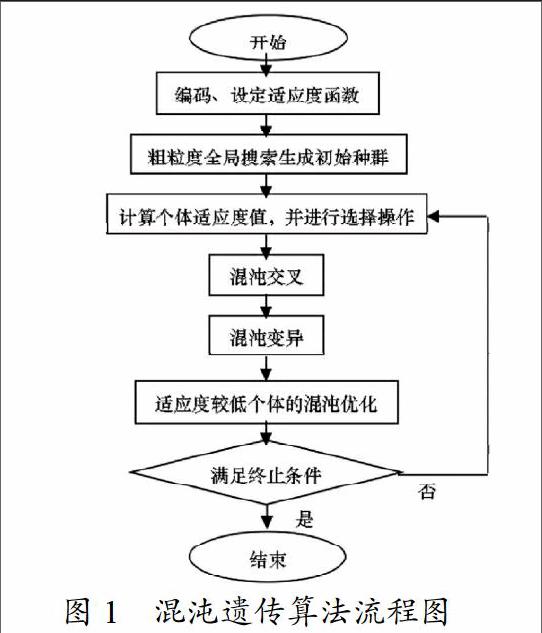
2.2 混沌遗传算法流程图 （图1）

3 实验结果及分析

为了验证本文算法在排课问题上优先于遗传算法。选择玉林师范学院2015-2016学年上学期排课任务为测试范例，其中种群数1000。对算法性能的考察指标包括平均运行时间、出现较优解的次数。

3.1 实验结果

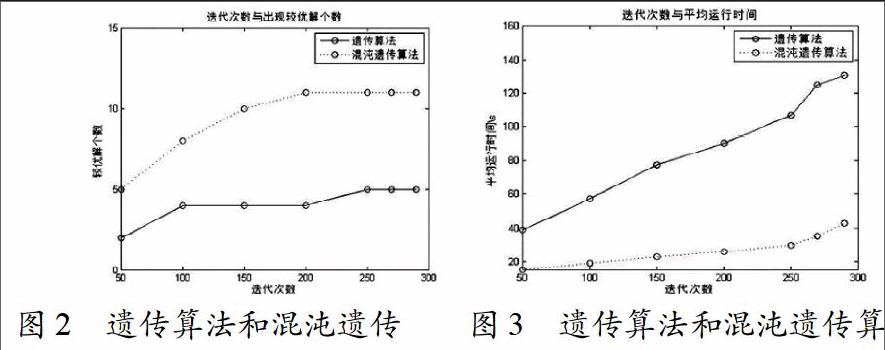
基于两种算法的高校排课方案，迭代次数分别设定为50、100、150、200、250、270、290，每次迭代50次进行测试，运行并记录结果。如图2、图3所示。3.2 实验结果分析

我们从两个方面来分析混沌遗传算法的有效性。首先从出现较优解的次数方面，随着迭代次数的增加，混沌遗传算法和遗传算法出现较优解的次数都趋于稳定，但是当迭代次数一定时，混沌遗传算法出现较优解的次数明显比遗传算法出现较优解的次数多出2倍。其次从收敛速度方面，实验表明，出现较优解的次数趋于稳定时，混沌遗传算法收敛速度比遗传算法的收敛速度快3倍。以上分析表明，本文采用的混沌遗传算法具有收敛速度快，易趋于全局最优解等特点，故该算法应用到排课问题上是有效可行的。

参考文献

[1] 李兵，蒋慰孙.混沌优化方法及其应用[J].控制理论与应用，1997.14（4）：613-615.

[2] 王东升，曹磊.混沌、分形及其应用[M].合肥：中国科学技术大学出版社，1995.

[3] 邹恩，李翔飞，陈建国.混沌控制及其优化应用[M].长沙：国防科技大学出版社，2002.