基于问题解决的物理模型教学的应用研究——以“弹力突变问题”为例

王胜华 侯 恕 周 瑜

(东北师范大学,吉林 长春 130024)

基于问题解决的物理模型教学的应用研究
——以“弹力突变问题”为例

王胜华 侯 恕 周 瑜

(东北师范大学,吉林 长春 130024)

“弹力突变问题”是高三复习“牛顿运动定律”专题中的难点、易错点.面对变化多端的弹力,由于学生对物理模型及其物理特征理解不透,难以把握弹力问题特点和一般的分析方法,导致错误.本文以理想绳为例,阐述了具体的物理建模过程,对弹力突变问题的模型进行了深入剖析,并给出了一般分析流程,最后给出了建模教学的优化策略,希望对一线教学有所帮助.

弹力突变问题;物理模型;刚性;轻质

1 问题的阐述

对“弹力突变问题”进行物理建模教学,既可以使学生的思维得到训练,帮助学生掌握分析问题的方法,同时运用模型解题又能提高学生的问题解决能力.通过物理建模教学,可帮助学生迅速提炼出题目中的关键信息,提高解题效率.但是,在实际教学中,教师忽略了对学生建模思想的培养、对建模方法的引导,只是注重应用模型解题,不强调注重理解,导致学生对模型的建立过程,模型的特征、使用条件模糊掌握,遇到新的题型还是不会建模.

2 如何构建理想绳的模型

在建立物理模型的过程中要注重模型方法和建模思想的的掌握.下面以理想绳为例,探究建模的过程.

建模的方法:理想化方法.建模思想:突出主要因素,忽略次要因素.

构建模型的过程:

图1 物理建模的过程

2.1 确定研究对象

以生活中的弹性绳作为研究对象.弹性绳有质量,可以伸长,它只能产生沿着绳的收缩方向的拉力.当弹性绳在弹性限度内发生轴向形变时,产生的弹力大小由胡克定律计算.

2.2 理想化处理

2.2.1 不计质量

选一张紧绳中间任意一段为研究对象进行受力分析,设绳两边施加的弹力分别为F左、F右,将有F左-F右=Δma,若Δm≠0,则F左≠F右,这就意味着一根绳上取不同长度的绳为研究对象,导致绳上的弹力大小不同,这样绳上弹力大小的求解变得非常复杂.同时考虑到绳的质量比重物小的多,为突出弹性绳伸长时产生的弹力的特点,忽略绳的质量.若Δm=0,则F左=F右,绳两端的弹力大小相等.由于研究对象是在绳中任选的,因此,轻绳中各点弹力大小相等.

2.2.2 刚性介质

绳上可以产生弹力.弹力是发生形变的物体由于具有弹性而作用于与之接触的物体上的力,它的大小由物体的材料和接触处的形变程度决定.由于绳的劲度系数特别大,在受力时,形变量与绳长相比非常小,往往很难直接判断,因此,在处理绳的弹力问题时,忽略绳的形变,把它看成是不可伸长的刚性介质.

2.3 构建理想化模型

理想化的绳中的弹力大小相等.因此,存在自由端的轻绳上的弹力为0.

理想化的绳忽略其形变,则弹力变化过程的时间忽略不计,所以理想化的绳可以发生突变.同时,绳上弹力的大小就不能由形变量求解,大小无法直接求出,只能由主动力和物体所处的运动状态决定,满足被动力的特点.

所以理想绳是轻质的、刚性绳,满足的特点是:绳中各点弹力大小相等,可以发生突变,无自由端的理想绳上的弹力大小由主动力和物体所处的运动状态决定,有自由端的理想绳上的弹力为0.

2.4 运用模型解决问题

图2

如图2所示,一质量为m的物体,系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断,求剪断瞬间物体的加速度.

下面是某学生对该题的一种解法.

解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在3力作用下保持平衡T1cosθ=mg,T1sinθ=T2,T2=mgtanθ.剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanθ=ma,所以加速度a=gtanθ,方向在T2反方向.

你认为这个结果正确吗?请对该解法作出评价并说明理由.

解析:错误.这道题考察对“理想绳的模型”的掌握．剪断l2的瞬间,出现自由端,T2突变为0,同时无自由端的绳上弹力T1也要发生突变,但是T1的大小由物体的重力和瞬间的运动状态决定.当绳剪断瞬间,物体将以悬点为圆心做圆周运动.由于速度为0,则在法向上重力的法向分量与T1平衡,物体只有切线方向的合外力,则mgsinθ=ma,所以加速度a=gsinθ,方向垂直于线l1斜向下.

物理模型的建构是为了方便探讨事物的本质,将研究问题简单化的抽象描述.在模型的建构过程中,教师要强化学生的物理模型的意识,注重方法,引导学生面对变化的题目分析主要和次要因素,抓住问题的本质,建立模型.在习题课中,要注意模型知识的正迁移,注重将模型与具体的物理情景联系在一起．

3 弹力突变问题模型全析

在高中阶段,弹力突变问题中常见的物理模型有理想绳、理想杆、刚性接触面和理想弹簧.

3.1 刚性介质模型的弹力突变特点

对于理想杆模型的建构,我们忽略了杆的质量,认为它是刚性的.所以,理想杆模型的特点是:杆中各点弹力大小相等,可以发生突变,无自由端的理想杆上的弹力大小由主动力和物体所处的运动状态决定,有自由端的理想杆上的弹力为0.

对于接触面模型的建构,我们忽略了它的形变,认为它是刚性的,所以,刚性接触面模型的特点是:弹力可以发生突变,它的大小由主动力和物体所处的运动状态决定.

在弹力突变问题中,以上3种模型可以总结为——刚性介质模型.这个模型的特点是:当介质有自由端时,弹力可突变为0;当介质无自由端时,弹力可以突变,而且突变后弹力的大小由物体受到的其他力和物体所处的运动状态决定.

3.2 轻弹簧模型的弹力突变特点

对于理想弹簧模型的建构,我们忽略了弹簧的质量.由于弹簧形变量很大,形变恢复需要一定的时间,因此,弹簧弹力不发生突变.所以,理想弹簧模型的特点是:弹簧中各点弹力大小相等,一般不可以发生突变,有自由端的理想弹簧的弹力为0,无自由端的理想弹簧上的弹力大小由胡克定律计算.

常见的轻弹簧突变问题也可分成以下两种情况:

当介质是有自由端的轻弹簧时,弹力可以发生突变为0.由轻质模型的特点可知,弹簧弹力为0;

当介质是无自由端的轻弹簧时,弹力不能发生突变.无自由端的轻弹簧的弹力属于主动力.主动力是主动使物体运动或有运动趋势的力,这一类力有其“独立自主”的大小和方向,不受物体所受其它力的影响,一般可以彼此独立地提前测定.

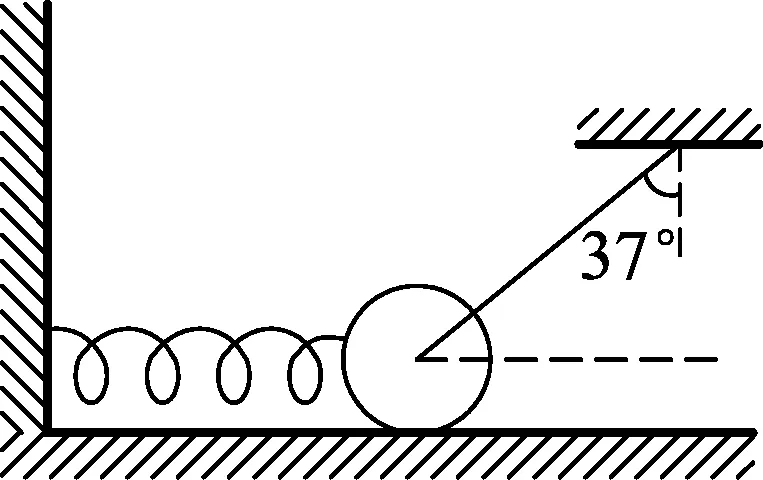
图3

3.3 模型的应用

如图3所示,在光滑水平面上有一质量为1kg的物体,它的左端与一劲度系数为800N/m的轻弹簧相连,右端连接一细线.物体静止时细线与竖直方向成37°,此时物体与水平面刚好接触但无作用力,弹簧处于水平状态,则下列判断正确的是

(A) 当剪断细线的瞬间,物体的加速度为7.5m/s2.

(B) 当剪断细线的瞬间,物体所受合外力为0.

(C) 当剪断细线的瞬间,地面给物体的支持力为0.

(D) 当剪断弹簧的瞬间,物体的加速度为7.5m/s2.

解析:设绳上拉力为T1,弹簧弹力为T2,地面给物体的支持力为N,物体重力为mg,则刚开始时,T1sin37°=T2,T1cos37°=mg,N=0,T2=mgtan37°.当剪断细线的瞬间,出现自由端,T1突变为0,理想弹簧弹力T2不突变,地面给物体的支持力N发生突变.由于物体将向右做加速运动,物体在竖直方向上处于平衡状态,N突变为mg.所以,mgtan37°=ma,a=gtan37°=7.5m/s2,所以选项(A)正确,选项(B)、选项(C)错误.当剪断弹簧的瞬间,出现自由端,T2突变为0,绳上弹力T1突变,物体收到的支持力N发生突变.由于物体没有运动趋势,绳上弹力T1突变为0,N突变为mg,选项(D)错误.

对于这道题,学生可能会选择(A)选项,但是不知道“为什么剪断细线时地面给物体的支持力可以突变为mg”.学生对于剪断弹簧的瞬间物体的受力及运动状态难以确定,不明白“为什么剪断弹簧时绳上弹力突变为0”,原因是没有将模型与具体的物理情景结合在一起,没有掌握模型建构的方法和解题的一般分析过程.

3.4 弹力突变问题的分析流程

通过以上对模型的介绍及应用,可总结出遇到弹力突变问题时的分析流程，如图4所示.

图4 突变问题分析流程

4 物理建模教学的优化策略

引导学生理解物理模型,教学中注重物理模型意识的渗透.教师要讲清楚为什么要建模,物理模型的特点; 重视模型建立的过程与方法;采用变式训练,促进知识正迁移;注重模型应用的一般分析过程.在高三物理学习过程中,有的学生经常遇到新的题型或者稍微变换物理情景的题目就不会做了,可能是因为对知识点及其本质没有掌握,或者没有将零碎的知识点进行整合,因此,开展物理建模教学很有意义.在进行建模之前,教师要对模型的建构方法、内容有一个全面的掌握,对学生的易错点有预知,才能更好的实施教学.在课堂上,教师要引导学生掌握建模的方法,充分了解物理模型的物理特征、领会其中丰富的物理涵义,并给出一般分析过程,这样才能收获更好的复习效率,提高学生的分析问题的能力.因此,建议教师在高三复习课堂上一定要讲清楚“什么是、是什么、为什么和怎么做”.

1 陈燕琴,陈佳静.意味深长的“轻质”[J].物理教师,2016,37(3):77-79.

2 张强.如何解决“绳”和“弹簧”的突变类问题[J].物理通报,2011(1):16-18.

2016-10-10)