复矩阵方程组的Hermite解
2017-03-30胡志增杨春花
胡志增,杨春花
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
复矩阵方程组的Hermite解
胡志增,杨春花
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)

复矩阵方程;有限迭代算法;共轭;Hermite解
线性系统理论中出现大量的矩阵方程,所以对于怎样求解矩阵方程的研究是十分必要的,也是必须的。对矩阵方程的求解方法也已经有了许多研究,其中Kronecker积是一个重要的方法。但是在求解大型矩阵时会对内存有较高的要求,舍入误差也可能更大,所以迭代求解法在求解矩阵方程中开始出现。很多工作者用迭代法求解矩阵方程[1-7],但是还有很多的问题需要进一步研究。
对于矩阵A,B∈Cm×n,如果〈A,B〉=0,就说A和B正交。如果对于矩阵序列A1,A2,A3,…,Ak成立〈Ai,Aj〉=0 (i≠j),就称这个矩阵序列是正交的。
问题1:对于给定的矩阵A1,A2∈Cp×m,B1,B2∈Cm×q,C1,C2∈Cp×m,D1,D2∈Cm×q,M1,M2∈Cp×q,求矩阵X∈HCm×m,使得
(1)
下面,建立一种迭代算法,求解矩阵方程组(1)的Hermite解。
1 预备知识
首先给出一个从复数空间到实数域R的内积,所定义的这个内积在本文中是十分重要的。而实数域内积的定义参看文献[8]。
定理1.1 定义从空间Cm×n到实数域R的内积为〈A,B〉=Re[tr(AHB)],其中A,B∈Cm×n,则所定义的内积是一个内积空间。下面用(Cm×n,R,〈·,·〉)表示这个内积空间。
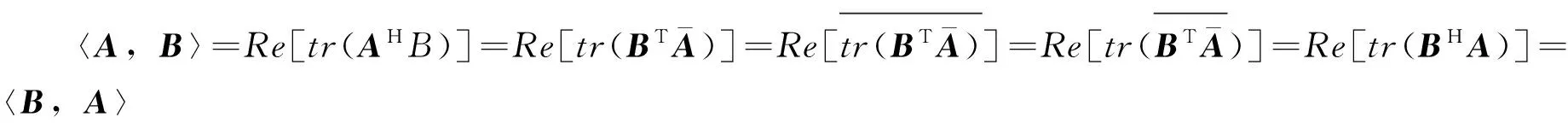
(2)对任意实数α,矩阵A,B,C∈Cm×n,很容易得到下列结果
〈αA,B〉=Re[tr((αA)HB)]=Re[tr(αAHB)]=Re[αtr(AHB)]=αRe[tr(AHB)]=α〈A,B〉。
〈A+B,C〉=Re[tr((A+B)HC)]=Re[tr(AH+BH)C)]=〈A,C〉+〈B,C〉。
(3)显然tr(AHA)>0,当A≠0时。所以〈A,A〉=Re[tr(AHA)]>0对所有A≠0均成立。
上述定理中的证明说明从空间Cm×n到实数域R的所定义的内积满足内积空间的条件,所以说(Cm×n,R,〈·,·〉)是一个内积空间。
2 求Hermite解方程组的迭代算法
算法2.1
第1步:输入矩阵A1,A2∈Cp×m,B1,B2∈Cm×q,C1,C2∈Cp×m,D1,D2∈Cm×q,M1,M2∈Cp×q以及任意初始矩阵X1∈HCm×m
第2步:计算
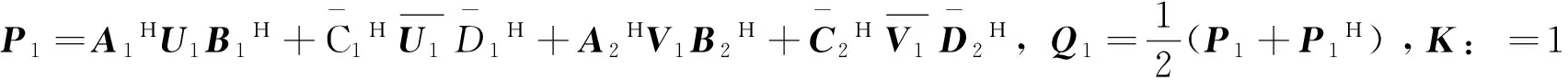
第3步:计算
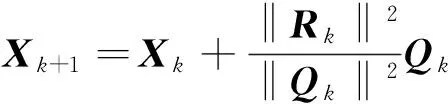
第4步:计算
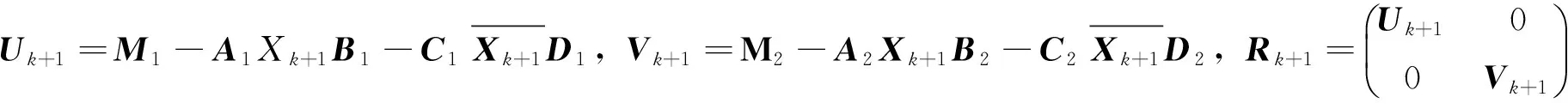
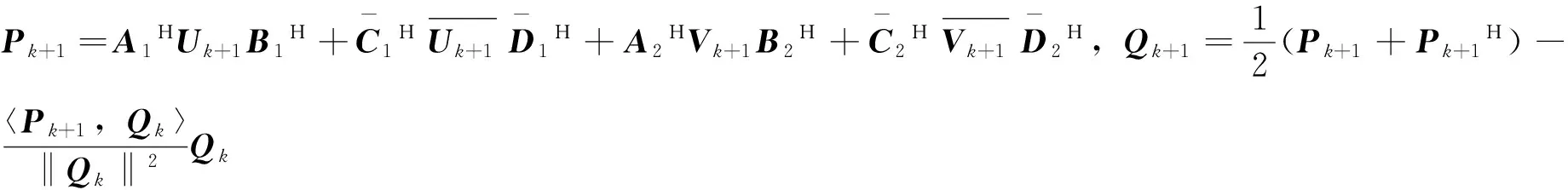
如果Rk+1=0或者Rk+1≠0,Qk+1=0,则停止,否则,令k:=k+1,回到第2步继续计算。
为了证明算法2.1的收敛性,首先验证以下一些基本的性质。
引理2.1 对于由算法2.1所产生的矩阵序列{Ri},{Pi},{Qi},有下列等式成立:
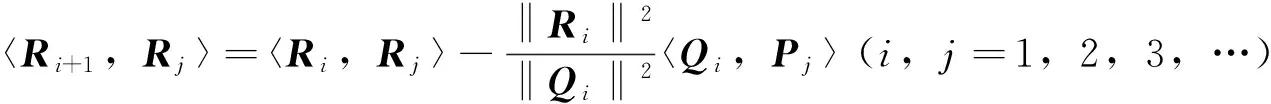
(2)
证明:由算法2.1可知
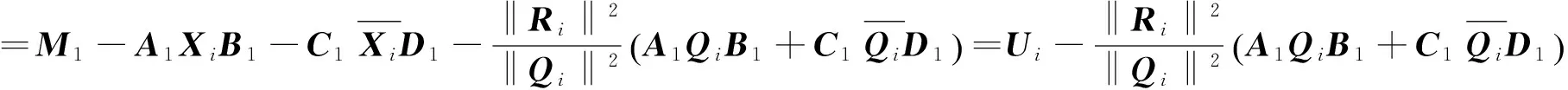
(3)
同理有
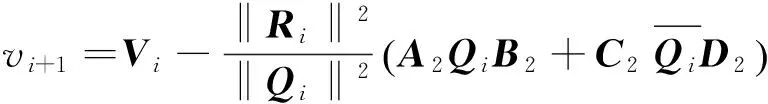
(4)
由此

(5)
而
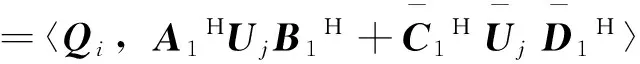
(6)
所以
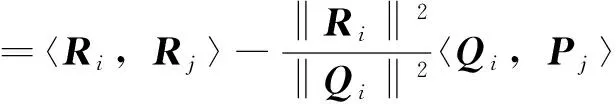
(7)
因此结论成立。
引理2.2 对于由算法2.1所产生的矩阵序列{Ri}、{Pi}、{Qi},当k≥2时有下列等式成立:
〈Ri,Rj〉=0,〈Qi,Qj〉=0 (i,j=1,2,3,…,k)。
(8)
证明:当k=2时,而Q1H=Q1,由引理2.1以及迭代算法可知
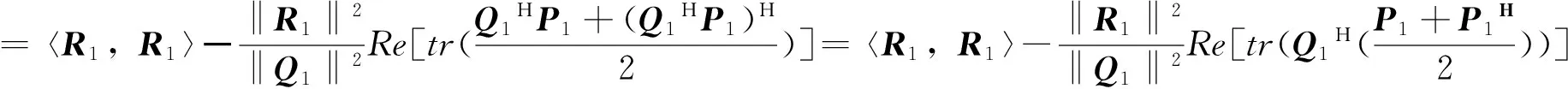

(9)
即有〈R2,R1〉=0成立,同理可证〈Q2,Q1〉=0成立。
假设式(8)对所有k=s成立,注意到QsH=Qs,〈Qs,Qs-1〉=0,由引理2.1可知
=‖Rs‖2-‖Rs‖2=0。
(10)
同理可证
〈Qs+1,Qs〉=0。
(11)
当j=1时,容易通过引理2.1验证〈Rs+1,Rj〉=0。对于j=2,3,…,s-1,由假设〈Rs,Rj〉=0,〈Qs,Qj〉=0,〈Qs,Qj-1〉=0,由引理2.1和迭代算法,可以证得:
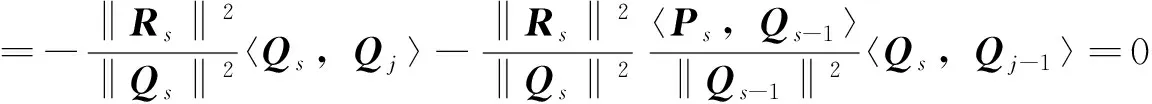
(12)
和
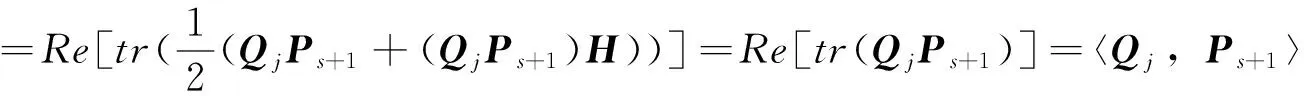
(13)
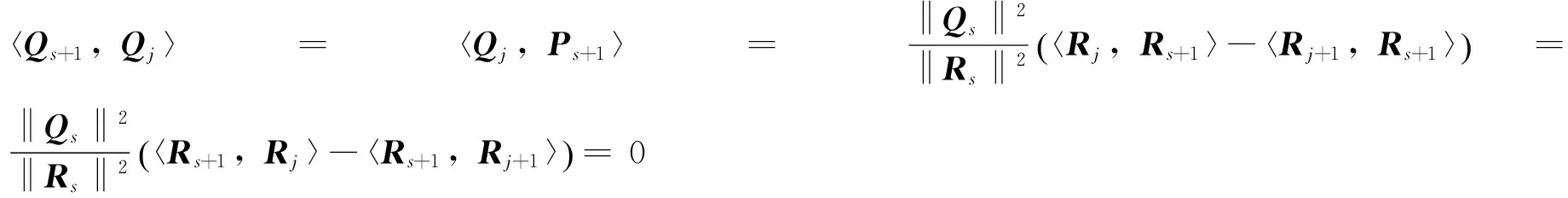
(14)
也就是说式(10)对k=s+1也成立,所以由归纳法可知引理3.2成立。
引理3.3 假设方程组(1)是相容的,X*是方程组的任意一个解,则
〈X*-Xk,Qk〉=‖Rk‖2,k=1,2,3,…
(15)
证明:当k=1时,注意到(X*-X1)H=X*-X1,所以
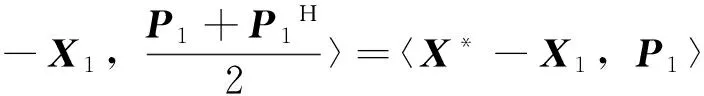

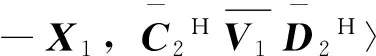
(16)
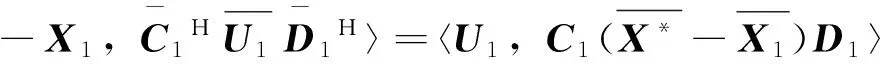
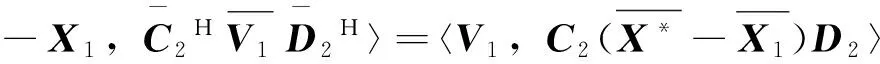
所以〈X*-X1,Q1〉=‖R1‖2,假设当k=s时成立〈X*-Xs,Qs〉=‖Rs‖2,
易证

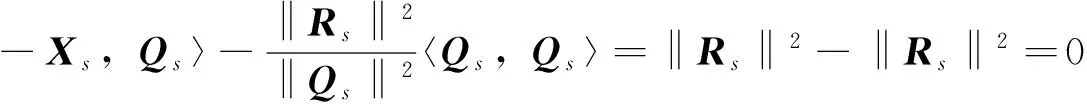
(17)
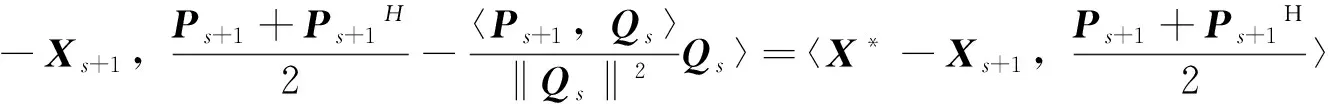
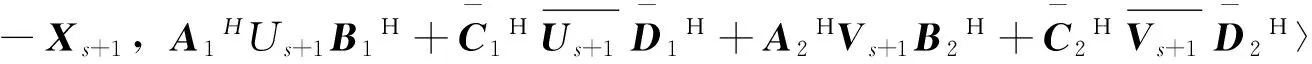
=〈Us+1,Us+1〉+〈Vs+1,Vs+1〉=‖Rs+1‖2。
(18)
由归纳法可知结论成立。
定理1 假设方程组(1)相容,对任意初始矩阵X1∈HCm×m,则通过所建立的算法最多迭代2pq+1步即可求出方程组的解。
证明:假设Ri≠0,i=1,2,…,2pq,通过引理2.3可知Qi≠0,i=1,2,…,2pq,所以可以通过所建立的算法得到X2pq+1,R2pq+1,且由引理2.2可知〈Ri,Rj〉=0i,j=1,2,…,2pqi≠j,也就是说{Ri}i=1,2,…,2pq对于定义在复数域上的内积空间(Cm×n,R,〈·,·〉)是正交矩阵列。由引理2.3可知〈R2pq+1,Ri〉=0i=1,2,…,2pq,由所定义内积空间的维数可知必有R2pq+1=0,所以X2pq+1就是方程组(1)的解。证毕。
3 数值举例
在这一部分,将给出两个例子来验证所给算法的有效性,试验中都采用MATLAB R2012a进行计算。由于计算误差的影响,当‖T‖<ε=10-2时,就认为T=0。但是随着问题计算规模的不同,可以适当取的更大或更小。
例:对于问题1,给定矩阵A1,A2,B1,B2,C1,C2,D1,D2,M1,M2如下


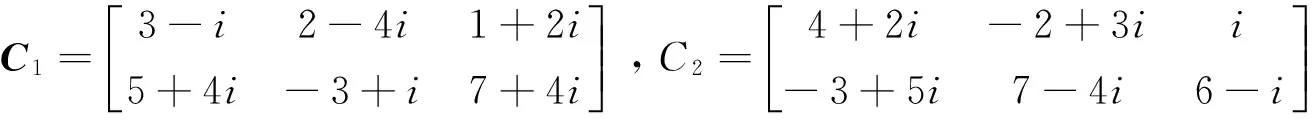
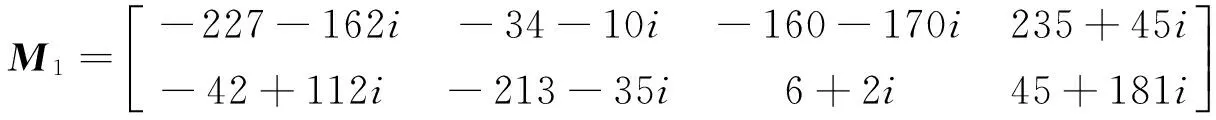
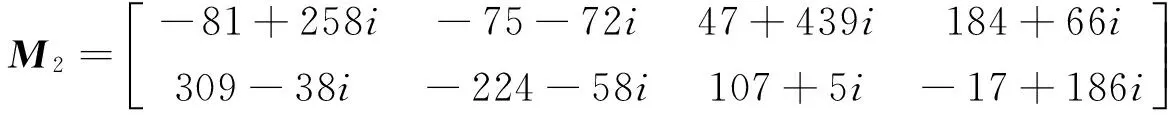
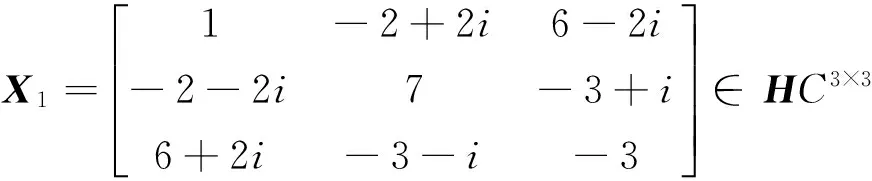
4 结 语
[1]LiangK,LiuJ.Iterativealgorithmsfortheminimum-normsolutionandtheleast-squaressolutionofthelinearmatrixequationsA1XB1+C1XTD1=M1,A2XB2+C2XTD2= M2[J].AppliedMathematicsandComputation,2011,218:3166-3175.
[2]WuAG,FengG,DuanGR,etal.Finiteiterativesolutionstoaclassofcomplexmatrixequationswithconjugateandtransposeoftheunknowns[J].MathematicalandComputerModelling,2010,52:1463-1478.
[3]PengYX,HuXY,ZhangL.AniterativemethodforsymmetricsolutionsandoptimalapproximationsolutionofthesystemofmatrixequationsA1XB1=C1,A2XB2=C2[J].AppliedMathematicsandComputation,2006,183:1127-1137.
[4]PengYX,HuXY,ZhangL.AniterationmethodforthesymmetricsolutionsandtheoptimalapproximationsolutionofthematrixequationAXB=C[J].AppliedMathematicsandComputation,2005,160:763-777.
[5]WangMH,ChengXH,WeiMS.IterativealgorithmsforsolvingthematrixequationAXB+CXTD=E[J].AppliedMathematicsandComputation,2007,187:622-629.
[6]PengZY.AniterativemethodfortheleastsquaressymmetricsolutionofthelinearmatrixequationAXB=C[J].AppliedMathematicsandComputation,2005,170:711-723.
[7]WuAG,ZengXL,DuanGR,etal.IterativesolutionstotheextendedSylvester-conjugatematrixequations[J].AppliedMathematicsandComputation,2010,217:130-142.
[8] 张贤达,矩阵分析与应用[M].北京:清华大学出版社,2004:23-35.
HermiteSolutionstoClassofComplexMatrixEquations
HUZhizeng,YANGChunhua
(XiangtanUniversity,Xiangtan411105,China)
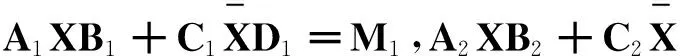
complexmatrixequations;finiteiterativealgorithms;conjugate;hermitesolution.
2016-09-14
胡志增(1991-),男,河南安阳人,在读硕士研究生,主要从事最优控制理论与计算方面的研究.
10.3969/i.issn.1674-5403.2017.01.022
O151.24
A
1674-5403(2017)01-0084-05
