关于Pell方程x2-18y2=1与y2-Pz2=16公解的研究
2017-03-30赵建红
赵 建 红
(丽江师范高等专科学校数学与计算机科学系,云南 丽江 674199)
关于Pell方程x2-18y2=1与y2-Pz2=16公解的研究
赵 建 红
(丽江师范高等专科学校数学与计算机科学系,云南 丽江 674199)
目的 Pell方程的公解是数论中的一个重要问题。设P=2p1…ps(1≤s≤4),p1,…,ps(1≤s≤4)是互异的奇素数,关于Pell方程组x2-18y2=1与y2-Pz2=16的整数解的初等解法至今仍未解决。方法 主要利用同余的性质、Pell方程解的性质和递归序列等方法。结果 得出Pell方程组x2-18y2=1与y2-Pz2=16仅当D=2×577时有非平凡公解(x,y,z)=(±19601,±4620,±136)。结论 推进了该类Pell方程组整数解的研究。
Pell方程;公解;整数解;同余;递归序列
Pell方程
x2-D1y2=m(D1∈Z+,m∈Z)与y2-D2z2=m(D2∈Z+,m∈Z)
(1)
是一类重要的方程,其公解问题一直受到数论爱好者的关注。目前主要结论集中在m=1,n=1及m=1,n=4,具体详见文献[1~8]。
m=1,n=16时Pell方程(1)成为:
x2-D1y2=1与y2-D2z2=16
(2)
关于Pell方程(2)的公解的情况,目前无相关结果。本文主要讨论D1=5,D2为偶数时Pell方程(2)的公解的情况,
即方程
x2-18y2=1 与y2-D2z2=16
(3)
公解的情况。
1 关键性引理
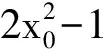
引理2[10]当a>0且是一个平方数时,方程ax4-by2=1至多只有一组正整数解。
引理3[11]若D是一个非平方的正整数,则方程x2-Dy4=1至多有1组正整数解(x,y),而且方程恰有2组正整数解的充要条件是D=1785或D=28560或2x0和y0都是平方数,这里的(x0,y0)是方程x2-Dy2=1的基本解。

证明 设(xn,yn),n∈Z是Pell方程x2-18y2=1的整数解,若xn=a2,代入方程x2-18y2=1得a4-18y2=1。由引理1知,方程a4-18y2=1仅有平凡解(a,y)=(±1,0),此时xn=1,从而n=0;反之,显然。
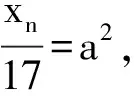

2 定理及证明
定理 设P=2p1…ps(1≤s≤4),p1,…,ps(1≤s≤4)是互异的奇素数,
则Pell方程
x2-18y2=1与y2-Pz2=16
(4)
当D=2×577时有非平凡公解(x,y,z)=(±19601,±4620,±136)和平凡公解(x,y,z)=(±17,±4,0);当D≠2×577时仅有平凡公解(x,y,z)=(±17,±4,0)。
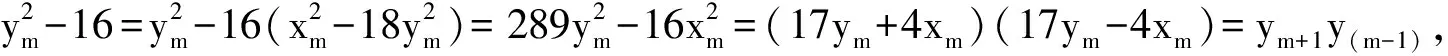
即
(5)
由(4)式得
Pz2=ym+1ym-1
(6)
设(x1,y1)为Pell方程x2-18y2=1的基本解,则有(x1,y1)=(17,4),故Pell方程x2-18y2=1的全部整数解为:
容易验证以下性质成立:
(Ⅰ)xn≡1(mod2),x2n≡±1(mod17) ,x2n+1≡0(mod17);
(Ⅱ)y2n+1≡4(mod),y2n≡0(mod17),y2n+1≡±4(mod17);
(Ⅲ)gcd(xn,yn)=1,gcd(xn,xn+1)=1,gcd(yn,yn+1)=4;
(Ⅳ)gcd(x2n,y2n+1)=gcd(x2n+2,y2n+1)=1,gcd(x2n+1,y2n)=gcd(x2n+1,y2n+2)=17;
(Ⅴ)xn+2=34xn+1-xn,x0=1,x1=17;yn+2=34yn+1-yn,y0=0,y1=4。
情形1m为偶数

则(6)式为
(7)
(7)式右边为平方数的奇数倍。又P=2p1…ps(1≤s≤4),p1,…,ps(1≤s≤4)是互异的奇素数,则(7)式左边为平方数的偶数倍,显然矛盾,故(7)式不成立,此时Pell方程(4)无公解。
情形2m为奇数
令m=2k+1,K∈Z则(7)式为
Pz2=y2ky2(k+1)
(8)
由y2k=2xkyk,y2(k+1)=2xk+1yk+1知,
(8)式可化为
Pz2=4xk+1yk+1xkyk
(9)

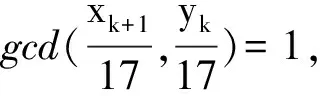

情形2.1k为偶数
令k=2l,l∈Z,此时(9)式为
Pz2=4x2l+1y2l+1x2ly2l
(10)
由y2l=2xlyl知,(10)式可化为
Pz2=8x2l+1y2l+1x2lxlyl
(11)




即
(12)
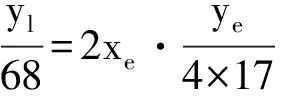
l=1时,由(Ⅴ)式知,(11)式为Pz2=8x1x2x3y1y3=8×4×17×577×4620×19601=27×5×7×11×172×577×1153,则P=2×3×5×7×11×577×1153,z=8×17,与“P=2p1…ps(1≤s≤4),p1,…,ps(1≤s≤4)是互异的奇素数”相矛盾,故此时方程(11)无整数解,因此Pell方程(4)无公解。
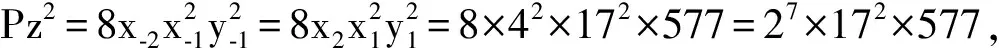
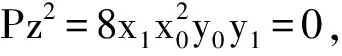
情形2.2 为奇数
仿情形2.1的证明可知此情形Pell方程(4)仅有平凡公解(x,y,z)=(±17,±4,0)。
综上所述,定理得证。
[1]Ljunggren W.Littom Simultane Pellske Ligninger[J].Norsk Mat Tidsskr,1941,(23):132-138.
[2]胡永忠,韩清.也谈不定方程组x2-2y2=1与y2-Dz2=4[J].华中师范大学学报:自然科学版,2002,36(01):17-19.
[3]管训贵.关于Pell方程x2-2y2=1与y2-Dz2=4的公解[J].华中师范大学学报:自然科学版,2012,46(03):267-269+278.
[4]贺腊荣,张淑静,袁进.关于不定方程组x2-6y2=1,y2-Dz2=4[J].云南民族大学学报:自然科学版,2012,21(01):57-58.
[5]杜先存,管训贵,杨慧章.关于不定方程组x2-6y2=1与y2-Dz2=4的公解[J].华中师范大学学报:自然科学版,2014,48(03):5-8.
[6]杜先存,李玉龙.关于不定方程x2-6y2=1与y2-Dz2=4的公解[J].安徽大学学报:自然科学版,2015,39(06):19-22.
[7]过静,杜先存.关于不定方程x2-12y2=1与y2-Dz2=4的解[J].数学的实践与认识,2015,45(09):289-293.
[8]过静,杜先存.关于Pell方程x2-30y2=1与y2-Dz2=4的公解[J].数学的实践与认识,2015,45(01):309-314.
[9]朱卫三.x4-Dy2=1有解的充要条件[J].数学学报,1998,28(05):681-683.
[10]乐茂华.一类二元四次不定方程[J].云南师范大学学报:自然科学版,2010,30(01):12-17.
[11]Walsh G.A note on a theorem of Ljunggren and the Diophantine equationsx2-kxy2+y4=1 orx2-kxy2+y4=4 [J].Arch Math,1999,73(2):501-514.
[责任编辑:关金玉 英文编辑:刘彦哲]
Common Solution to Pell Equationsx2-18y2=1 andy2-Pz2=16
ZHAO Jian-hong
(Department of Mathematics and Computer Science,Lijiang Teachers College,Lijiang,Yunnan 330013,China)
Objective The common solution to Pell equations is a very important problem of Number theory.LetP=2p1…ps(1≤s≤4),whereps(1≤s≤4) are distinct odd primes,the common solution to Pell equations ofx2-18y2=1 andy2-Pz2=16 still remains unresolved.Methods Congruence,some properties of the solutions to Pell equation and recursive sequence were used.Result The Pell equations in the title have two nontrival common solutions only whenD=2×577.Conclusion These results promote the study of the kind of Pell equations.
Pell equation;common solution;integer solution;congruence;recursive sequence
云南省教育厅科研基金项目(2014Y462);红河学院校级课题(XJ15Y22)
赵建红(1981-),男,云南巍山人,副教授,硕士,研究方向:数学教育及数论。
O 156.1
A
10.3969/j.issn.1673-1492.2017.01.001
来稿日期:2016.06.20
