水库水温数学模型适用性研究

邱进生，邓云，颜剑波，脱友才，梁瑞峰

(1.中国电建集团中南勘测设计研究院有限公司，湖南长沙 410014；2.四川大学水力学与山区河流开发保护国家重点实验室，四川成都 610065)

水库水温数学模型适用性研究

邱进生1，邓云2，颜剑波1，脱友才2，梁瑞峰2

(1.中国电建集团中南勘测设计研究院有限公司，湖南长沙 410014；2.四川大学水力学与山区河流开发保护国家重点实验室，四川成都 610065)

利用水库水温数学模型掌握水库的水温分层规律及下泄水温过程，是工程环境影响预测和水库水质管理的重要手段。水库水温预测数学模型较多，国内对水库水温预测模型的应用大多是单个模型在个案中的研究，不同模型的适用性比较研究相对较少。选择现有5种较为常用的水库水温预测数学模型，包括垂向一维模型、立面二维模型WWL和CE-QUAL-W2，以及三维模型MIKE3和EFDC，利用典型湖泊型水库——东江和河道型水库——三板溪的实测资料，对模型进行对比验证和参数率定。根据计算结果，并结合模型的简化假定、紊流模式和数值计算方法，探讨了5种模型的适用性和局限性，并对不同类型的水库推荐了适宜的水库水温预测方法。

水库水温模型；模型参数；适用性

水库筑坝蓄水调节径流的同时也改变了河道的水温情势，对库区及下游农田灌溉、鱼类生长繁殖等都会产生不利影响，准确预测水库水温结构及其对下游的影响是工程环境影响评价的重要内容。水库水温数学模型预测方法是基于物理机制建立描述水体流动和水流传热的数学物理方程，利用数值计算方法来模拟水库水温结构与下泄水温过程。水库水温模型研究最早始于20世纪60年代的美国，经历了垂向一维、立面二维、三维的发展过程。

最早的垂向一维水温模型为WRE模型和MIT模型[1-2]，模型中考虑了水库入流、出流及水面热量交换，之后增加了风力掺混的修正形成了混合层模型，混合层模型在冷却水系统和水库水质模拟等方面得到了较多的应用。李怀恩[3]提出一个包括入库泥沙影响的水库垂向水温预测模型。陈永灿[4]建立适用于密云水库的垂向一维水温模型对水温进行预测，以实测资料率定了模型参数，并较好地模拟出密云水库的水温变化规律及影响要素。立面二维模型可以较好地模拟纵垂向温差浮力流的运动与水温分层形成发展过程，适用于河道相对狭长的水库水温的模拟。CE-QUAL-W2是美国陆军工程兵团开发的河道纵垂向二维水动力学水温水质模型，国内外均得到广泛应用。Nortan[5]将CE-QUAL-W2应用于水库水质管理中，分析了气象要素对水温的影响。李艳[6]运用紫坪铺库区实测资料进行了验证和模型参数率定，库区水温的模拟结果和实测值吻合良好。邓云[7-8]等建立了适用于大型深水库的宽度平均立面二维水温模型，采用浮力修正的κ-ε模型，得到了水库物理模型、二滩水库等实测资料的良好验证，并应用于雅砻江下游梯级电站的水温累积影响研究。近年三维水库水温数学模型也开始得到应用，目前应用较多的软件有美国的EFDC、丹麦的MIKE3和荷兰的DELFT3D等。国内张士杰[9]等利用MIKE3分别对漫湾水库和二滩水库库区水温进行了模拟计算。龙国庆[10]、李兰[11]等利用EFDC分别对二滩水库和漫湾水库的库区水温进行了模拟计算，取得了较好的效果。

本次研究将针对典型河道型水库(三板溪)和湖泊型水库(东江)开展5种不同模型的对比研究，进行模型参数率定和敏感度分析，并对模型进行验证，分析各模型的适用性和局限性，并对不同类型的水库推荐适宜的水库水温预测方法。

1 依托水电工程概况

1.1 东江水库(湖泊型)

东江水电站位于湖南资兴县境内耒水流域上游，库区属亚热带季风气候区，多年平均气温17.1 ℃。坝址控制流域面积4719 km2，多年平均流量144 m3/s，年平均径流总量45.4亿m3，水库正常蓄水位285 m，总库容81.2亿m3，具有多年调节能力，年库水替换次数为0.56，为稳定分层型水库。从2007年4月12日至2007年12月31日进行了坝前和下泄水温观测，以此开展模型验证，边界调节采用东江水库2007年4月12日至2007年12月31日的逐日气象、逐日坝前水位和入库流量，由于没有同步监测入库水温，因此采用建库前的多年平均逐日天然坝址水温。

1.2 三板溪水库(河道型)

三板溪水电站位于沅水干流上游河段的清水江中下游，所处流域属亚热带季风气候区，库区多年平均气温15.6～16.7 ℃。坝址控制流域面积11 050 km2，多年平均年径流量约75.69亿m3。水库正常水位475.00 m，相应库容37.48亿m3，最大坝高185.5 m，具有多年调节能力，年库水替换次数为2.0次，为稳定分层型水库。从2013年5月5日至2014年9月2日进行了坝前和下泄水温观测，以此开展模型验证，计算边界为三板溪水库2013年5月5日至2014年9月2日的逐日气象、入出库流量和入库水温。

2 垂向一维水温模型及适用性分析

垂向一维水温模型假定水温只在垂向上存在变化，在同一水平层温度相同。因此模型中把水体沿垂向上划分为一系列的水平薄层，忽略水平薄层中温度的变化，热交换只沿垂向进行，对任一水平薄层进行热量平衡分析。模型中考虑了水面热交换、入流、出流、热扩散、热对流等因素的影响。

2.1 模型计算结果

英格曼迅速抬起脸，看着少佐微垂着头，眉眼毕恭毕敬。他一把夺过请柬，打开信封，不祥的预感使他患有早期帕金森症的手大幅度颤抖。少佐让一个士兵给神甫打手电照明。请柬是发给唱诗班的女孩的。

图1比较了东江水库不同月份坝前垂向水温的实测值与计算值，模型能较好地模拟出湖泊型水库坝前水温的分布特征，其表温层、温跃层、滞温层的厚度基本与实测值一致。图2比较了东江水库在整个计算期间下泄水温的实测值与计算值，4—7月计算值与实测值吻合得非常好，8—12月计算值稍高于实测值，平均误差为0.3 ℃。对于湖泊型水库，全库区水温基本都符合水平面水温均匀的假定，忽略纵向变化不会带来很大误差，同时由于流动弱，从而出入流对温度场的扰动小，流场假定带来的误差较小。因此垂向一维模型在东江水库验证中精度较高，适用性强。

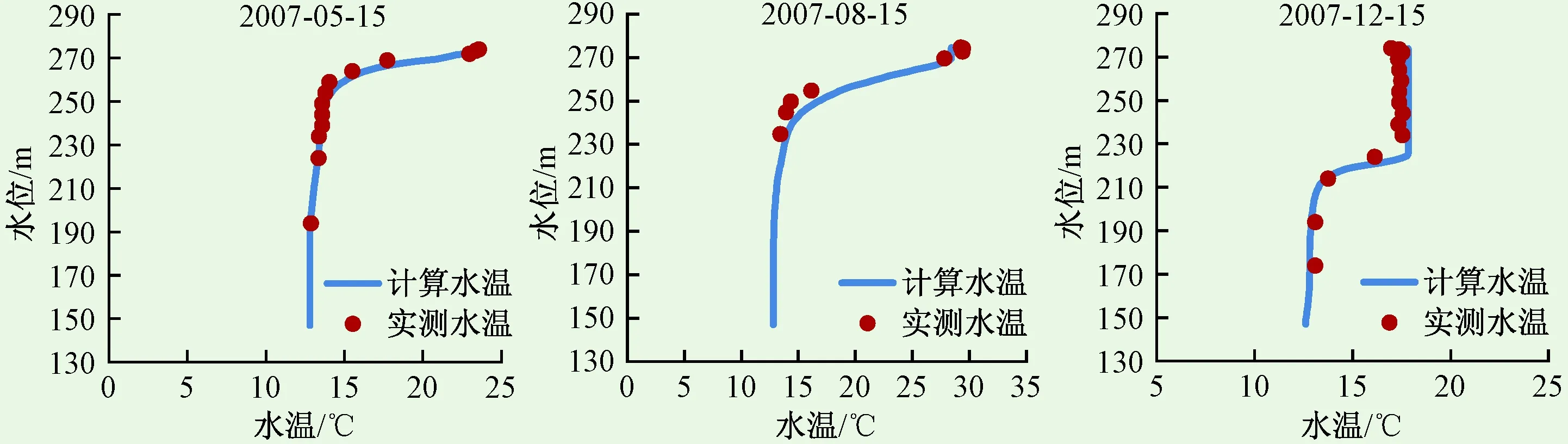
图1 东江水库坝前垂向水温实测值与计算值对比Fig.1 The measured vertical water temperature in front of Dongjiang reservoir dam compared with the calculated value

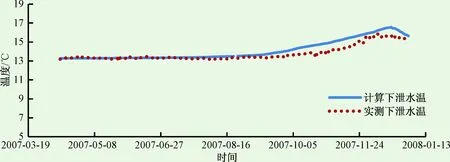
图2 东江水库下泄水温实测值与计算值对比Fig.2 The measured discharge water temperature of Dongjiang reservoir compared with the calculated value

2.2 模型主要参数设置及敏感性分析

表面热通量的计算是表层水温计算的关键。太阳辐射水体表面吸收率β主要影响水体表层水温，建议取值范围为0.4～0.7。太阳辐射在水体中的衰减系数η主要反映太阳辐射影响水体的厚度，与水体的色度和浊度相关，取值范围为0～1 m-1。垂向紊动扩散的计算是垂向水温结构模拟的关键，垂向扩散系数与流场分布、温度梯度、风速、泥沙等因素相关，需采用经验公式或实测资料的率定结果。在本次东江水库的水温计算中，经过参数率定后，β取0.7，η取0.35 m-1，垂向扩散系数取3.0×10-6m2/s。

2.3 模型适用性分析

垂向一维模型边界条件相对简单，计算比较快速稳定。模型能较好地模拟湖泊型水库坝前垂向水温分层结构，整体上能够模拟出下泄水温的变化趋势，但由于忽略了纵向上的变化、简化的流场计算以及水位剧烈变化时的紊动，在对回水长度有较明显纵向分布的水库，以及入出库流量较大(调节性能较弱)的水库，这些假定和简化均会带来较大误差。因此，垂向一维模型更适合于流量相对较小、回水较短的湖泊型水库。

3 立面二维模型验证及适用性分析

WWL(West Water-Lateral)是四川大学开发的宽度平均立面二维水温分析系统，采用k-ε双方程紊流模式，考虑温差浮力对垂向动量方程的影响，模型采用笛卡尔直角坐标系。

CE-QUAL-W2模型的垂向动量方程经过简化处理，忽略了时变加速度项、位变加速度项和湍流剪应力项，采用静水压力假定，模型提供了6种垂向涡流粘滞系数计算公式用于模拟不同特征水域，本次研究采用其推荐的W2N公式，模型采用笛卡尔直角坐标系。

图3比较了WWL模型和CE-QUAL-W2模型得到的三板溪水库坝前垂向水温计算值和实测值，可知5—8月的升温期由于受太阳辐射和入库水温的共同影响，库区水温分层逐渐显著，预测结果在表温层、斜温层和底部低温层的厚度与位置都与实测值基本吻合，说明模型能很好地模拟出库区浮力流动与大气热交换对稳定分层水库分层结构变化的影响。WWL模型对底表层水温均模拟较好，CE-QUAL-W2模型计算得到的底层水温略有偏高。

图4比较了WWL模型和CE-QUAL-W2模型计算下泄水温与实测坝下水温及坝址多年平均水温，表明计算得到的下泄水温过程与出库水温过程趋势一致，预测结果与实测值都表现出较高的精度，WWL模型和CE-QUAL-W2模型误差均在0.3 ℃以内。

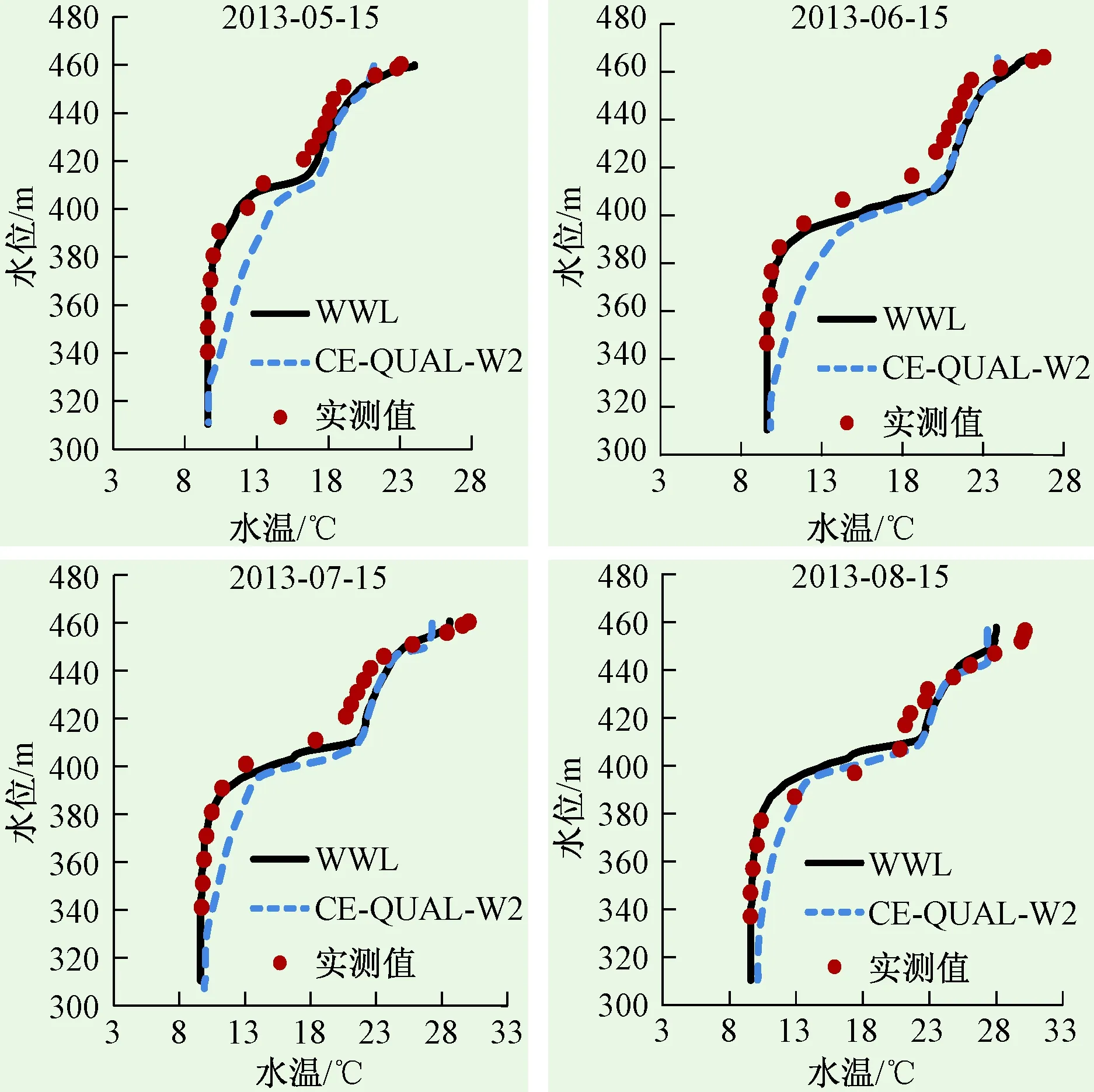
图3 三板溪水库坝前垂向水温实测值与计算值对比Fig.3 The measured vertical water temperature in front of Sanbanxi reservoir dam compared with the calculated value

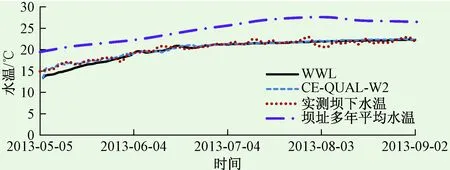
图4 下泄水温实测值与计算值对比Fig.4 The measured discharge water temperature of Sanbanxi reservoir compared with the calculated value

3.2 模型主要参数设置及敏感性分析

WWL模型设计的参数主要为热通量参数——太阳辐射表面吸收系数β和太阳辐射在水体中的衰减系数η，一般β的取值范围为0.4～0.7，η为0～1 m-1，本次模型率定后分别取0.6和0.45。CE-QUAL-W2模型中需要重点率定的参数有风遮蔽系数和动态光遮蔽系数。动态光遮蔽系数用于修正植被和地形对太阳辐射的遮蔽，风遮蔽系数用于修正测点风速与库区实际风速的差异，在山区和/或植被茂盛的地区，风遮蔽系数取0.5～0.9；而在地形开阔地区，风遮蔽系数取1.0；风遮蔽系数取值超过1.0，以反映陡峭河岸的漏斗效应。本次研究中动态光遮蔽系数和风遮蔽系数分别取1.0和1.5。

3.3 模型适用性分析

验证结果显示，WWL模型和CE-QUAL-W2模型均适用于长而相对较窄、在纵向和垂向上存在明显温度变化的分层型水库，对水库垂向水温分层结构和下泄水温过程均有很好的模拟效果。WWL模型由于采用了精度较高的紊流双方程模式及完整垂向动量方程，对计算网格和计算时长有所限制，计算成本相对增加。CE-QUAL-W2模型由于对垂向动量方程进行了简化，在垂向加速度比较大时，如因降温期冷水下沉或升温期来流快速上浮等存在较大垂向加速度的情况下，其模拟精度有所降低。立面二维模型忽略了流场、温度场在宽度方向的变化，不适用于宽浅的湖泊型水库。

4 三维水温模型验证及适用性分析

MIKE系列软件可用于模拟河流、湖泊、水库、河口和外海的水流、水质及泥沙传输问题。共有3种网格结构，分别是单一矩形网格、矩形嵌套网格和非结构化网格。计算中对比采用了单一矩形网格和非结构化网格。EFDC是一个多任务、高集成的环境流体动力学模块式计算程序包，可建立河流、湖泊、水库、湿地、河口、海洋等水系统的模型。EFDC模型网格主要包括笛卡尔网格、河流曲线网格和曲线正交网格3种类型。本次计算中采用了曲线正交网格。

4.1 模型计算结果

对于MIKE3模型，采用非结构化网格，计算时段为2013年5月5日至8月31日，计算结果如图5所示。计算结果表明坝前垂向水温基本处于同温状态，而实测结果显示三板溪为稳定分层水库，8月垂向温差超过19 ℃，计算与实测结果差异很大。验证情况显示MIEK3非结构化网格系统虽然对复杂边界条件和自由水位变化均具有较好的模拟能力，但对垂向分层水域的水温模拟效果差。采用结构化网格，且为避免垂向网格数过少对计算准确性产生影响，选取水位变动较小的2013年6月25日至8月25日，计算结果如图6所示。计算时段内计算结果与实测结果的垂向水温结构变化趋势基本一致，库底的低温水未受扰动而保持稳定，而取水口以上的区域为流动层，受入库水体及大气热交换的影响，温度分层逐渐加强，模型较好地模拟了这一过程，但斜温层的水温计算值较实测值有所偏高。

对于EFDC模型，计算时段为2013年5月5日至6月6日，如图7所示。计算结果显示在垂向上出现了较大的扩散导致表层水温偏低，而底层水温明显偏高且有显著的增温趋势，至模拟结束，底层水温已升至15.8 ℃，比实际情况高6.2 ℃。由此看来，模拟结果并未体现出水温稳定分层的特点，对于水库水温垂向分层现象的模拟效果并不理想。季振刚[12]分析认为，σ坐标系对处理变化陡峭的地形时，容易产生较大的附加数值耗散，由于水温分层的抑制作用，热量在垂向紊动扩散量小，累积的数值扩散显著加大了垂向扩散，引起水温误差明显。

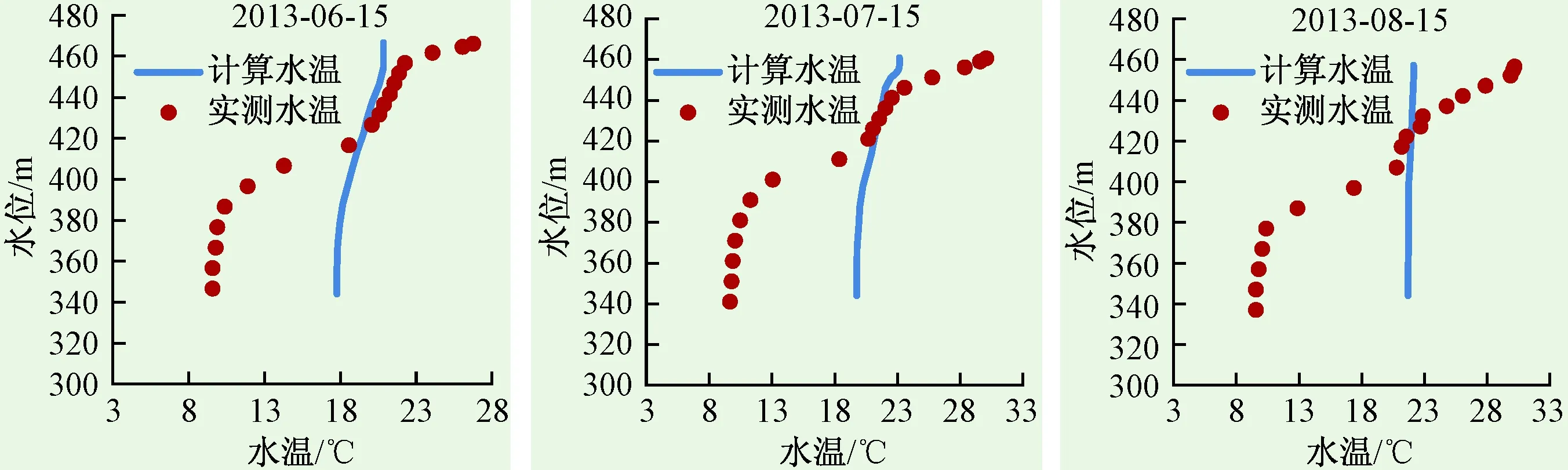
图5 三板溪水库坝前垂向水温实测值与计算值对比图(MIKE3非结构化网格)Fig.5 The measured vertical water temperature in front of Sanbanxi reservoir dam compared with the calculated value (MIKE3 unstructured grids)

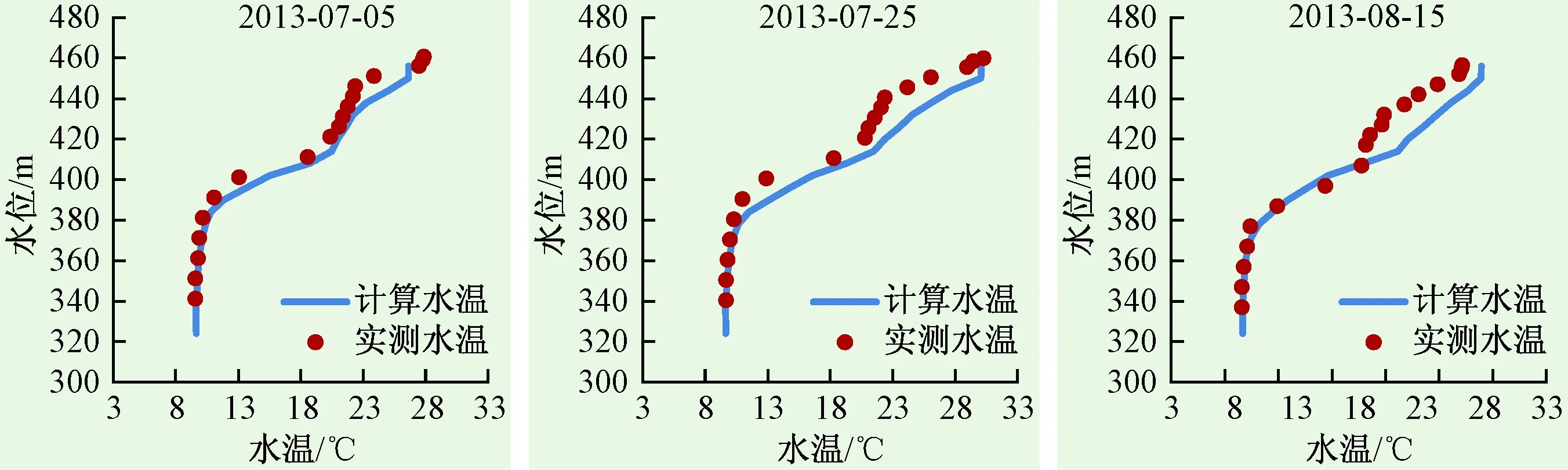
图6 三板溪水库坝前垂向水温实测值与计算值对比图(MIKE3结构化网格)Fig.6 The measured vertical water temperature in front of Sanbanxi reservoir dam compared with the calculated value (MIKE3 structured grids)

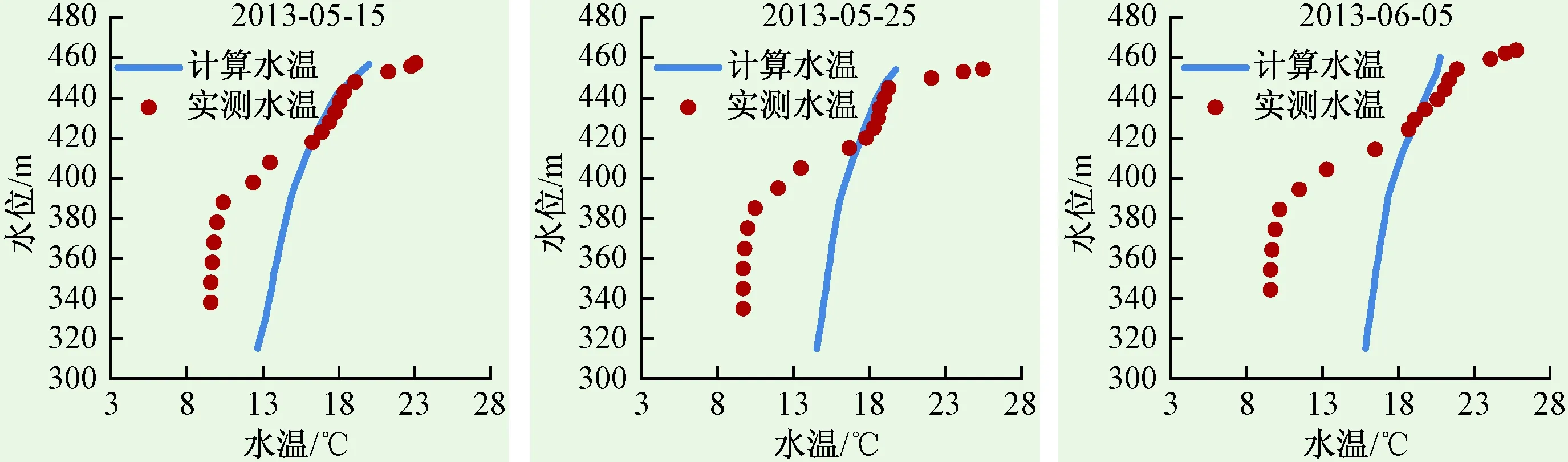
图7 三板溪水库坝前垂向水温实测值与计算值对比图(EFDC，三维)Fig.7 The measured vertical water temperature in front of Sanbanxi reservoir dam compared with the calculated value (EFDC, three-dimensional)

4.2 模型适用性分析

三维模型在建模过程中对地形资料要求较高，非结构化网格能够拟合复杂边界，但在求解过程中存在较大的数值扩散，导致垂向扩散过于显著，特别是对于窄深型水库无法模拟出稳定的水温分层结构，更适用于具有复杂边界且垂向分层不明显的浅水水域。结构化网格对存在水温分层水库的模拟效果优于非结构化网格，能模拟出较为稳定的分层垂向水温。

5 结论

本文通过对5种不同水温模型的方程、紊流模式及数值计算方法进行分析，得出各模型的适用性，并对主要计算参数取值进行了分析。垂向一维水温模型适用于稳定分层且库水替换较弱的湖泊型水库，垂向扩散系数是模型的敏感参数。立面二维模型WWL和CE-QUAL-W2均适用于长而相对较窄、在纵向和垂向上存在明显温度变化的分层型水库，采用完整的垂向动量方程和精细的紊流模式能取得更准确的模拟效果。三维模型对全库区水温的模拟仍存在较大困难，建议在特别关注水温横向差异的局部区域，如取水口附近、支流汇口等进行局部范围的三维模拟，并采用结构化网格。σ坐标系更适用于浅水水域，在模拟复杂边界时，易引入附加扩散而导致垂向水温计算误差偏大。

本研究仅对有限案例进行了模型比较分析，下一步需要针对更多不同调节性能和自然环境的水库案例进行对比分析，才能更好地明确模型适用性范围。

[1] Orlob G T. Mathematical modeling of water quality: streams, lakes, and reservoirs[M]. Chichester, UK: Wiley, 1983.

[2] Harleman D R F. Hydrothermal Analysis of lakes and reservoirs[J]. Joumal of the Hydraulics Division, 1982, 108(3): 301- 325.

[3] 李怀恩, 沈晋. 一维垂向水库水温数学模型研究与黑河水库水温预测[J]. 西安理工大学学报, 1990(4): 236- 243, 308.

[4] 陈永灿, 张宝旭, 李玉梁. 密云水库垂向水温模型研究[J]. 水利学报, 1998(9): 15- 21.

[5] Norton G E, Bradford A. Comparison of two stream temperature models and evaluation of potential management alternatives for the Speed River, Southern Ontario[J]. Journal of Environmental Management, 2009, 90(2): 866- 878.

[6] 李艳. CE-QUAL-W2在紫坪铺水库的应用及其参数敏感性分析[J]. 长江流域资源与环境, 2011, 20(11): 1274- 1278.

[7] 邓云. 大型深水库的水温预测研究[D]. 成都: 四川大学, 2003.

[8] 邓云, 李嘉, 李克锋, 等. 梯级电站水温累积影响研究[J]. 水科学进展, 2008, 19(2): 273- 279.

[9] 张士杰, 彭文启. 二滩水库水温结构及其影响因素研究[J]. 水利学报, 2009(10): 1254- 1258.

[10] 龙国庆, 刘召平, 梅志宏, 等. 季调节深水大库全库区全年水温结构的模拟验证[J]. 水利学报, 2011(1): 33- 39.

[11] 李兰, 武见. 梯级水库三维环境流体动力学数值预测和水温分层与累积影响规律研究[J]. 水动力学研究与进展A辑, 2010(2): 155- 164.

[12] 季振刚. 水动力学和水质——河流、湖泊及河口数值模拟[M]. 李建平, 冯立成, 赵万星, 等译. 北京: 海洋出版社, 2012.

Study on Applicability of Mathematical Models of Reservoir Water Temperature

QIU Jin-sheng1, DENG Yun2, YAN Jian-bo1, TUO You-cai2, LIANG Rui-feng2

(1.Power China Zhongnan Engineering Corporation Limited, Changsha 410014, China;2.State Key Lab of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China)

Mathematical models of reservoir water temperature were used to analyze the stratification rule of reservoir water temperature and the process of discharge water temperature, which are important means to predict the environmental impact of projects, and manage the quality of reservoir water. Nowadays, there are many mathematical models of reservoir water temperature prediction. However, the domestic applications of reservoir water temperature prediction are mostly based on single model in individual cases. The comparative study on the applicability of different models is very rare. In this paper, five common models of reservoir water temperature prediction were compared, including one vertical one-dimensional model, two vertical two-dimensional models-WWL and CE-QUAL-W2, as well as two three-dimensional models-MIKE3 and EFDC. Based on the measured data of typical lake-like reservoir-Dongjiang and river-like reservoir-Sanbanxi, these models were verified, and the model parameters were calibrated. Based on calculation results, simplifying assumptions, turbulence models and calculation methods of the models, the applicability and limitation of each model were discussed respectively. The suitable models of water temperature prediction were recommended for different types of reservoirs.

model of reservoir water temperature; model parameter; applicability

2016-02-27

论文成果依托中电建“水库水温预测模型及应用技术研究”科技项目支撑

邱进生(1964—)，男，江西抚州人，教授级高级工程师，主要研究方向为水利水电工程环境保护，E-mail：139630502@qq.com

邓云(1972—)，女，四川蓬溪人，研究员，博士，主要研究方向为环境与生态水利，E-mail：dengyun@scu.edu.cn

10.14068/j.ceia.2017.02.015

X820.3；TV697.2

A

2095-6444(2017)02-0057-06