预应力纤维加固管线的屈曲理论分析研究★

王懿鑫 王汝恒 贾 彬

(西南科技大学土木工程与建筑学院，四川 绵阳 621010)

预应力纤维加固管线的屈曲理论分析研究★

王懿鑫 王汝恒 贾 彬

(西南科技大学土木工程与建筑学院，四川 绵阳 621010)

基于大挠度理论与小挠度理论，推导了管道在预应力作用下的临界屈曲方程，并通过理论应用分析了影响临界屈曲的因素，结果表明：径厚比和钢管等级对钢管的临界屈曲影响较大，随着径厚比的降低，钢管等级的提高，临界屈曲应力也得到提高。

钢管,临界屈曲,大挠度理论，小挠度理论

0 引言

钢管在运行过程中，可能受到多种荷载作用，多年运行之后，难免会发生破坏。现如今，国内外对于存在缺陷的管道进行修复或者提高管道承受内压能力的方法很多，例如焊接修复补强类型，夹具修复补强类型，内衬修复补强类型[1]。近年来，采用预应力纤维加固损伤钢管的技术受到了人们的青睐[2,3]。采用预应力FRP加固钢管，不仅可以提高钢管承受内压的能力，还能恢复结构变形。随着现代技术的发展，如今工程所用的管道其强度越来越高，厚度越来越薄，由于钢管在正常运行中，还受到了诸如土压力、温度应力等的作用，而钢管在预应力作用下，综合各类荷载，可能会发生屈曲问题。

目前针对管道问题的研究主要集中在管道在外压作用下、轴向荷载作用下的临界屈曲研究，以及探讨影响管道临界屈曲的主要因素。孙彦彦[4]通过有限元分析方法，对钢管在内压和弯曲载荷联合作用下的数值仿真计算，发现径厚比、内压、钢级对临界屈曲应变有较大影响；张华等人[5]通过量纲分析获得了临界压缩屈曲应变公式和弯曲临界屈曲应变公式，并分析了影响临界屈曲应变的主要因素；李明哲[6]采用有限元手段分析了失稳因素对管道截面稳定性的影响，发现水平挠度是判定管道截面稳定性的重要指标；Bresses[7]运用小变形理论，对薄壁圆环在均匀外压下的临界屈曲进行了研究，并得出薄壁圆环在均匀外压作用下的临界屈曲公式；Fairbairn[8]对薄壁钢管在均匀外压下的屈曲进行了试验研究，管道的径厚比对于薄壁管道承受均匀外压的临界屈曲起着主要作用。

预应力作用下，当达到或超过管道承受的临界压力时，由于管道具有薄壁特点，属于薄壳结构，管道圆形截面不稳定，管道径向方向产生较大变形，在管道的运行过程中，可能会受到局荷载的作用，使得管道发生局部屈曲问题。在外压作用下传统的研究

方法是基于小挠度理论，未考虑初始屈曲和管线变形时的几何非线性的影响；本文采用小挠度理论和大挠度理论对预应力纤维加固钢管的临界屈曲展开研究，分析二者的差异性，并对影响管道的临界屈曲的相关因素进行探讨。

1 基于大挠度理论下的临界屈曲

判别临界状态的稳定准则分为两类，平衡的小稳定性准则和大稳定性准则。平衡的小稳定性准则以小挠度线性理论为基础，而后者是以大挠度为基础建立起来的稳定性准则。

设管道的半径为R，计算长度为R，对半径为R、长为L的圆柱壳沿轴向，径向采用右手坐标系，其内任一点P坐标的表示x,θ和z,x为该点到端部的轴向距离，θ为环向转角坐标，z为该点距中面的距离。另外,环向坐标还可用y表示，y=Rθ。其坐标建立如图1所示。

在体力素中，沿x,y方向的平衡方程中忽略剪切力的影响，在曲率改变中，忽略u,v位移的影响。

位移和荷载不成线性关系的弹性力学称为非线性弹性力学，引起非线性弹性力学的因素很多，主要是从几何变形关系、物理关系、平衡关系去进行分析。产生非线性的根源有两种：一是应变和位移之间的非线性；二是有限的变形物体需要根据变形后的关系建立平衡方程。而这都是属于集合非线性问题。在大变形的情况下，材料的应力—应变不再是线性关系，而是非线性关系，这类问题属于物理非线性。

钢管在预应力作用下其母线是水平的，并且平行于x轴，单元体是由两相邻母线和两垂直于母线的两个截面构成，其位置由x和角度θ决定，作用在单元体上的力如图2所示。

根据图2可得管道的平衡方程：

(1)

(2)

(3)

同理，可得单元体力矩平衡方程：

(4)

(5)

考虑初始曲率以及几何非线性的影响，可得弯曲中面应变方程：

(6)

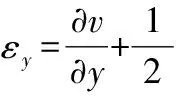
(7)

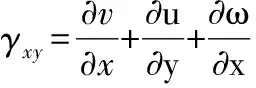
(8)

由应变方程可得中面应变变形协调方程：

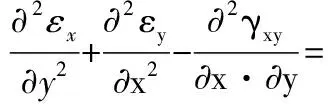
(9)

由胡克定律可知，弹性壳体的物理方程为：

(10)

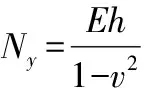
(11)

(12)

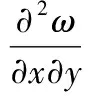
(13)

由变形协调方程、力和力矩平衡方程，可得管道屈曲时的控制微分方程：

(14)

设满足简支边界条件的屈曲挠度函数为：

(15)

其中，L为管道轴向方向的计算长度;R为管道半径。

由上可得管道能承受的极限预应力为：

(16)

(17)

基于大挠度理论，考虑初始曲率和变形后的弯曲变形的影响，建立了管道在预应力作用下的控制微分方程，通过简支边界条件的屈曲挠度函数，获得了管道在预应力作用下的屈曲控制方程。

2 基于小挠度理论下的临界屈曲公式

钢管在预应力作用下其母线是水平的，并且平行于x轴，单元体是由两相邻母线和两垂直于母线的两个截面构成，其位置由x和角度θ决定，作用在单元体上的力如图3所示。

由于不考虑初始曲率和管道弯曲变形后的影响，则其应变方程为：

(18)

(19)

由图3可得：

(20)

(21)

由胡克定律可得：

(22)

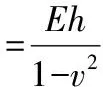
(23)

由对称性可知在圆周方向曲率没有变化。x方向的曲率为-d2ω/dx2,则有：

(24)

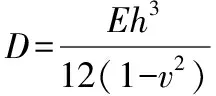
由此可得钢管的挠度微分方程为：

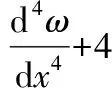
(25)

解此微分方程，并利用边界条件可得:

(26)

管道在荷载对称中心处取得极限应变：

(27)

而当ε=εmax，可求得极限外压q2:

(28)

3 理论应用及影响临界屈曲因素分析

为了探讨基于大挠度理论和小挠度理论之间是否存在较大差异，本文进行了案例应用分析，并探讨了影响管道在预应力作用下发生临界屈曲的相关因素。理论应用分析中，主要分析了径厚比、钢管等级对管道临界屈曲的影响。

目前服役管道的径厚比主要集中在30～100之间。据加拿大CSA S16.1—1994规定，当D/t≤13 000/Fy，管道在屈曲时全截面进入塑性状态；当D/t≤66 000/Fy，管道在截面全塑形弯矩发展前进入全塑性状态；当D/t≤18 000/Fy，管道破坏介于两者之间。为了使所研究的内容能包含以上3种失效类型，径厚比选择30,50,70,90。对钢管等级选择X42,X56,X65,X80(见表1)。

表1 工程工况

图4～图7表达的是通过大挠度理论和小挠度理论计算下的预应力极值的对比分析图，依据图4～图7可以看出，通过小挠度理论得出的结构均比通过大挠度理论计算的理论值较低，这是因为通过小挠度理论得出的公式未考虑管道的初始曲率的影响，并忽略了管道变形后对其产生的影响，所以最后的计算结果比通过大挠度理论计算出来的结果高一些，二者产生的误差均在5%～20%之间。

从图4～图7中可以看出，管道的径厚比对管道的屈曲影响很大，从图4～图7可以看出，随径厚比的增加，管道所承受的临界

屈曲应力呈线性降低，由此可见，管道的径厚比对管道临界屈曲影响较大。由于管道的刚度与管道厚度的三次方成正比，随着管道径厚比的增加，管道的厚度相较于管道的直径在减小，管道的刚度也在降低，而管道抵抗变形的能力也在降低。

钢管的临界屈曲应力随着钢管等级的增加而增加。管道的弹性模量和屈服强度随着钢管等级的增加而增加，而管道的刚度与管道的弹性模量成正比，随着管道等级的提高，材料的屈服强度也相应增加。所以，管道的整体刚度随管道等级的提高而提高，承受外压的能力也相应提高。

4 结语

本文采用理论应用分析的方法，对管道在预应力作用下的临界屈曲展开研究，分别采用大挠度理论和小挠度理论的分析方法，建立了管道在预应力下的临界屈曲公式，并对此进行了理论应用分析，得出结论如下：

1)本文建立了预应力纤维加固钢管的模型，基于大挠度理论，考虑初始屈曲和变形后的影响，建立了管道屈曲时的控制微分方程，依据简支边界条件的屈曲挠度函数方程，推导出了管道的临界屈曲方程；基于小挠度理论，不考虑初始屈曲和变形后的影响，建立了管道在预应力作用下的屈曲方程。

2)通过理论应用分析，比较了基于大挠度理论和小挠度理论得出的临界屈曲预应力极值，通过比较发现，基于小挠度理论的结算结果均比基于大挠度理论得出的结果高，二者差异在5%～20%之间。

3)径厚比是影响管道临界屈曲的关键因素，临界屈曲应力随着径厚比的增加而呈线性降低；对管道临界屈曲影响较为明显的因素还有钢管等级，随着钢管等级的提高，临界屈曲应力也相应提高。

[1] 张志伟.碳纤维布加固压力管道强度研究[D].绵阳：西南科技大学,2014.

[2] 卢亦焱.预应力FRP加固工程结构技术研究进展[J].中国工程科学,2008(8):40-44.

[3] 卢 毅.预应力玄武岩纤维布加固钢管的预应力损失研究[J].工业建筑，2015,45(6)：22-26.

[4] 孙彦彦.在内压和弯曲载荷下钢管临界屈曲应变的确定[J].油气储运,2013,32(9):1022-1026.

[5] 张 华.基于量纲分析的管道临界屈曲应变准则研究[J].焊管，2008,31(6)：90-93.

[6] 李明哲.大口径高等级钢埋地管道截面稳定性研究[D].成都：西南石油大学,2014.

[7] M.Bresse.Cours de mechaniqué,second edition,Paris,2007.

[8] W.Fairbrain.On the resistaince of tubes to collapse[J].Philophical transactions of the royal society of London，2012(148):389-413.

On buckling theory of prestressed fiber reinforcement pipelines★

Wang Yixin Wang Ruheng Jia Bin

(CollegeofCivilEngineeringandArchitecture,SouthwestUniversityofScienceandTechnology,Mianyang621010,China)

Based on the large deflection and small deflection theories, the paper induces the pipelines’ critical buckling equation, analyzes the factors affecting the buckling with the theories, and proves that the radius-thickness ratio and steel pipe grades have more influence on the critical buckling of the pipe and that the critical buckling stress increases along with the grades under the reduction of the radius-thickness ratio.

steel pipe, critical buckling, large deflection theory, small deflection theory

1009-6825(2017)05-0039-03

2016-12-04★:国家自然科学基金资助项目(51408513)；四川省科技计划资助项目(2014HH0062)

王懿鑫(1990- )，男，在读硕士

TU311

A