线性半向量二层规划问题乐观最优解的极点检验方法

刘敏，吕一兵，陈忠

(长江大学信息与数学学院，湖北 荆州 434023)

线性半向量二层规划问题乐观最优解的极点检验方法

刘敏，吕一兵，陈忠

(长江大学信息与数学学院，湖北 荆州 434023)

针对线性半向量二层规划问题的特殊结构，首先采用标量化技术将上述线性半向量二层规划问题转化为一般的二层单目标规划问题，然后采用以下层问题的Kuhn-Tucker最优性条件代替原问题的方法将其转化为含互补约束的优化问题，并取互补约束为罚项，构造相应的罚问题，同时分析罚问题最优解的性质，最后基于罚问题最优解的性质设计了线性半向量二层规划问题“乐观最优解”的极点检验方法。

半向量二层规划；罚函数；极点；乐观最优解

考虑如下线性半向量二层规划问题，

(1)

其中，x∈Rn,y∈Rm,b∈Rp,A1∈Rp×n,A2∈Rp×m,c∈Rn,c′∈Rm,D∈Rl×m。在上述半向量二层规划问题中，其下层问题：

(2)

为包含上层决策变量x的线性多目标优化问题。因此，对于给定的上层决策变量x，下层问题以有效解集或者弱有效解集的形式反馈给上层。由于下层问题的有效解集或者弱有效解集中的元素一般不是唯一的，这就意味着半向量二层规划问题本质上属于下层有不唯一最优解的一类二层规划问题。对于下层有不唯一最优解的二层规划问题，其最优解定义一般采用“乐观最优解”或者“悲观最优解”[1,2]。笔者考虑上述问题(1)的“乐观最优解”，即考虑如下线性半向量二层规划问题：

(3)

半向量二层规划最早由Bonnel 和Morgan在文献[3]中提出，近年来逐步引起了国内外研究者的关注。在线性半向量二层规划问题(3)的“乐观最优解”的研究方面，吕一兵和万仲平[4]以下层问题的互补约束为罚项，构造了罚问题并通过分析罚问题最优解的相关性质，设计了该类半向量二层规划问题的“乐观最优解”的全局优化算法；Ankhili和Mansouri[5]以下层问题的边缘函数为罚项，构造了相应的罚问题，证明了罚函数的精确性并给出了罚函数算法；Zheng和Wan[6]将上层目标函数估计值与下层问题的边缘函数同时作为罚项，提出了一种包含2个罚因子的罚函数方法，同时证明了罚函数的精确性；Calvete和Galve[7]将该类半向量二层规划问题转化为非凸约束域上的优化问题，并分别设计了Kth-算法及遗传算法，同时给出了数值实验结果；最近，Ren和Wang[8]将其转化为含对偶间隙约束条件的单层优化问题，构造出对偶间隙指标函数并取其为罚项，得到了相应的罚问题，证明了罚函数的精确性并设计了罚函数算法；另外，Lv和Wan[9]首先将该类半向量二层规划问题转化为非光滑优化问题，然后采用松弛技术逼近原问题的可行域，最后设计了求解原问题近似最优解的算法。下面，笔者针对线性半向量二层规划问题的特殊结构，采用标量化技术将上述线性半向量二层规划问题(3)转化为一般的二层单目标规划问题，构造了相应的罚问题，通过分析罚问题最优解的相关性质设计了线性半向量二层规划问题“乐观最优解”的极点检验方法。

1 相关定义及理论结果

记S={(x,y)|Ax+By≤b,x≥0,y≥0}为问题(3)的约束域，同时对于给定的上层决策变量x，记S(x)为下层问题(2)的弱有效解集。

定义1 若点(x,y)∈IR={(x,y)|(x,y)∈S,y∈S(x)}，则称(x,y)为问题(3)的可行解。

定义2 点(x*,y*)∈IR为问题(3)的局部最优解, 如果存在(x*,y*)的某个邻域U，使得对任意的(x,y)∈IR∩U,有cx+c′y≤cx*+c′y*。

为了确保所讨论的问题存在最优解，假设下列条件成立：

(A)问题(3)的可行域IR为非空紧集。

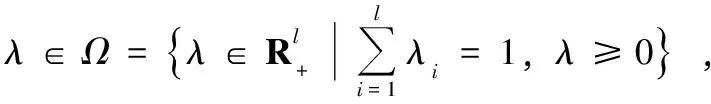
因此，问题(3)可以转化为：

(4)

在上述问题(4)中，以下层问题的最优性条件代替下层问题，可以将问题(4)转化为：

(5)

其中，u∈Rp,v∈Rm为Lagrange乘子。

问题(5)为带互补约束的线性规划问题，考虑将互补约束uT(b-A1x-A2y)=0,vTy=0作为罚项加入到上层目标函数，得到如下罚问题：

(6)

下面将分析问题(6)的最优解的相关性质，并以此为基础设计相应的求解算法。

记：

Z={(x,y)|A1x+A2y≤b,x≥0,y≥0}

且Zv,Wv分别表示集合Z,W的顶点集。

定理1 假设给定(λ,u,v)∈W以及罚因子K，问题：

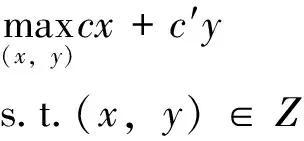
(7)

的某个最优解(x*,y*)可在集合Z的顶点处取得，即(x*,y*)∈Zv。

证明 对于给定的(λ,u,v)∈W以及罚因子K，问题(7)为线性规划问题。显然，问题(7)的某个最优解(x*,y*)∈Zv。证毕。

由定理1可以得到如下定理2。

定理2对于某个罚因子K，罚问题(6)的某个最优解(x*,y*,λ*,u*,v*)可在其可行域的顶点处取得，即(x*,y*,λ*,u*,v*)∈Zv×Wv。

证明 假设(x*,y*)∈Zv为问题(6)的某个最优解。对于问题(6)，由于其目标函数cx+c′y-K(uT(b-A1x-A2y)+vTy)为(λ,u,v)的线性函数，且W为多面体，则下列线性规划问题：

其某个最优解(λ*,u*,v*)必可在可行域W的顶点处取得，即 (λ*,u*,v*)∈Wv。证毕。

上述2个定理表明，罚问题(6)的最优解可以在其可行域的某个顶点处取得。下面将证明在罚问题(6)的最优解处，其罚项为零。

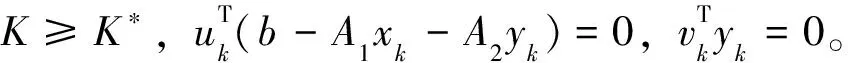
证明 假设(x*,y*,λ*)为问题(4)的最优解，则存在Lagrange乘子u*∈Rp,v*∈Rm，使得问题(4)的下层问题的最优性条件满足，即:

-(λ*)TD+(u*)TA2-(v*)T=0 (u*)T(b-A1x*-A2y*)=0 (v*)Ty*=0

假设点(xk,yk,λk,uk,vk)为问题(6)的最优解，则有：

简单运算后可得：

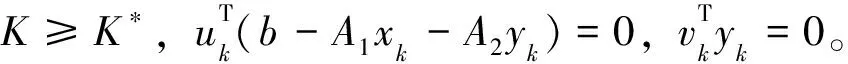
基于上述定理1、定理2和定理3，可以设计如下求解线性半向量二层规划问题“乐观最优解”的极点搜索算法。

2 算法

算法步骤如下：

步1 将线性半向量二层规划问题转化为问题(5)，同时采用相关方法求出Z和W的顶点集Zv,Wv。

步2 选择点(x,y,λ,u,v)∈Zv×Wv，且满足uT(b-A1x-A2y)=0以及vTt=0。

步3 将步1中得到的候选点分别带入上层目标函数，同时比较目标函数的值得到相应的最优解。

3 算例

为了说明算法的实现过程，考虑如下半向量二层规划问题[10]，文献中其最优解为(x,y,z)=(3,0,0)。

求出集合Z和W的顶点集：

Zv={(3,0,1),(1,0,2),(3,0,0),(0,1,2),(0,3,0)}

在上述顶点集中，选择使得互补条件uT(b-A1x-A2y)+vTy=0满足的组合。

将上述满足条件的顶点组合带入目标函数并比较大小可知，顶点(x,y,z)=(3,0,0)为上述线性半向量二层规划问题的最优解。

上述算例表明，笔者设计的极点检验方法对求解线性半向量二层规划问题是可行的。

4 结语

利用线性半向量二层规划问题的特殊结构，通过构造罚问题并分析其“乐观最优解”的相关性质设计了求解其“乐观最优解”的极点检验方法。简单的算例表明，所设计的算法是可行的。值得指出的是，笔者提出的算法依赖于多面体顶点的有效获取。然而，目前如何有效的获得多面体的全部顶点依然是一个具有挑战性的问题。倘若能够有效的获得多面体的全部顶点，那么所设计的算法将具有良好的计算前景。

[1]DempeS.Foundationsofbilevelprogramming[M].London:KluwerAcademicPublishers,2002.

[2]滕春贤,李智慧. 二层规划的理论与应用 [M].北京: 科学出版社,2002.

[3]BonnelH,MorganJ.Semivectorialbileveloptimizationproblem:Penaltyapproach[J].JournalofOptimizationTheoryandApplications, 2006, 31(3): 365～382.

[4]吕一兵，万仲平. 线性半向量二层规划问题的全局优化方法[J]. 运筹学学报，2015, 19(2):29～36.

[5]AnkhiliZ,MansouriA.Anexactpenaltyonbilevelprogramswithlinearvectoroptimizationlowerlevel[J].EuropeanJournalofOperationalResearch, 2009, 197(1):36～41.

[6]ZhengY,WanZM.Asolutionmethodforsemivectorialbilevelprogrammingproblemviapenaltymethod[J].JournalofAppliedMathematicsandComputing, 2011(37):207～219.

[7]CalveteHI,GaleC.Onlinearbilevelproblemswithmultipleobjectivesatthelowerlevel[J].Omega, 2011, 39(1):33～40.

[8]RenAH,WangYP.Anovelpenaltyfunctionmethodforsemivectorialbilevelprogrammingproblem[J].AppliedMathematicsModelling, 2016(40):135～149.

[9]LvYB,WanZM.Asolutionmethodfortheoptimisticlinearsemivectorialbileveloptimizationproblem[J].JournalofInequalitiesandApplications,2014:164.

[10]CalveteHI,GaleC.Onlinearbilevelproblemswithmultipleobjectivesatthelowerlevel[J].Omega, 2011(39):33～40.

[编辑] 洪云飞

2016-11-16

国家自然科学基金项目(11201039)。

刘敏(1979-)，女，硕士生，现主要从事最优化理论与算法方面的研究工作。

吕一兵(1979-)，男，博士，教授，现主要从事最优化理论与算法方面的教学与研究工作,30950045@qq.com。

O224

A

1673-1409(2017)01-0001-04

[引著格式]刘敏，吕一兵，陈忠.线性半向量二层规划问题乐观最优解的极点检验方法[J].长江大学学报(自科版)，2017,14(1)：1～4.