花岗岩残积土的土水特征曲线参数概率
2017-03-29罗小艳刘伟平
罗小艳++刘伟平

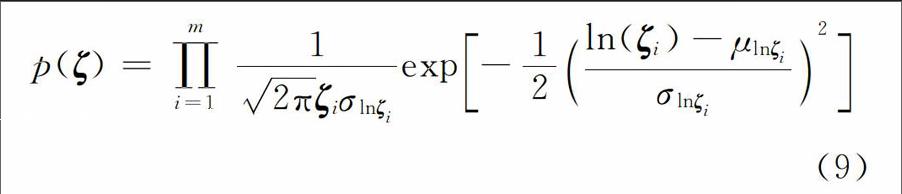

摘要:土水特征曲线(SWCC)用于描述非饱和土中含水量与基质吸力的关系,在非饱和土力学中具有重要的作用。在SWCC拟合模型中有多个拟合参数,各值通过实验方法获得且具有很大的不确定性。采用贝叶斯理论对拟合参数的不确定性进行分析,将SWCC拟合参数作为随机变量,采用Van Genuchten模型拟合花岗岩残积土的土水特征曲线试验数据。以马尔可夫链蒙特卡罗方法的延迟拒绝适应性算法获得模型参数后验分布抽样,获得了不同置信区间的SWCC及其对应参数值。
关键词:贝叶斯理论;土水特征曲线;马尔可夫链蒙特卡罗算法;花岗岩残积土;置信区间
中图分类号:TU411文献标志码:A文章编号:16744764(2017)01011206
收稿日期:20160916
基金项目:国家自然科学基金(51468041、 51268046);江西省自然科学基金(20161BAB203078);教育部博士点专项基金(20123601110001)
作者简介:罗小艳(1978),女,主要从事岩土工程可靠度研究,(Email)luoxiaoyan2@126.com。
刘伟平(通信作者),男,副教授,(Email)wpliu@126.com。
Received:20160916
Foundation item:National Natural Science Foundation of China (No.51468041, 51268046); Natural Science Foundation of Jiangxi (No. 20161BAB203078); PhD Programs Foundation of Ministry of Education of China (No. 20123601110001)
Author brief:Luo Xiaoyan (1978), main research interest: geotechnical engineering reliability, (Emial) luoxiaoyan2@126.com.
Liu Weiping (corresponding author), associate professor, (Email) wpliu@126.com.Probabilistic analysis of the soilwater characteristic
curve of granite residual soil
Luo Xiaoyan1,2,3,Liu Weiping1
(1.School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, P. R. China;
2. School of Civil Engineering and Architecture, Jiangxi Science and Technology Normal University,
Nanchang 330013, P. R. China;3. The University of Newcastle, NSW 2308, Australia)
Abstract:The soilwater characteristic curve(SWCC)could be used to describe the relationship between the water content and the matrix suction in unsaturated soil and played important roles in unsaturated soil mechanics. Several parameters in fitting models and significant uncertainty of SWCC were obtained by experiment. The uncertainty of SWCC fitting parameters was analyzed using the Bayesian theory. The curvefitting parameters were regarded as the random vectors. And the Van Genuchten model was used to fit the experimental data of SWCC for the granite residual soils. The posterior distributions of model fitting parameters were obtained by the Markov Chain Monte Carlo simulation delayed rejection adaptive metropolis. Confidence intervals of uncertain model parameters of SWCC were obtained by proposed approach.
Keywords:bayesian theory; soilwater characteristic curve; markov chain monte carlo; granite residual soils; confidence interval
土水特征曲線(SWCC)描述土中含水量或饱和度与基质吸力之间的关系,可以用来预测非饱和土中的渗透系数、抗剪强度、体积变化等[13]。由于每个测量点需要长时间去使基质吸力平衡,土水特征曲线试验耗时很长。通常只能在有限的数据的基础上对土水特征曲线进行拟合。为了有效地预测土水特征曲线,不同的土水特征曲线的拟合方法和模型被提出。土水特征曲线广泛应用到非饱和土工程的数值分析中,SWCC拟合参数输入的可靠性直接影响着数值结果的正确性。
由于土水特征曲线受影响因素很多,土的种类、试验方法、环境因素等都会使土水特征存在明显的差异性。土水特征曲线的试验数据与拟合参数也就具有明显的不确定性。Phoon等 [4]采用四项Hermite展开式对砂土的土水特征曲线进行概率分析。谭晓慧等[5]、徐全等[6]分别对UNSODA数据库的非饱和土、合肥非饱和土的土水特征曲线进行了概率和敏感性分析。为了分析模型参数不确定性,拟合参数可以作为随机变量[7]。土水特征曲线的计算模型参数不易确定,该模型的预测精度严重影响边坡稳定性分析的可靠性。
目前,在岩土工程随机分析中,贝叶斯方法主要用于土的抗剪强度[8]、渗流参数[9]、固结系数[10]等问题的分析中。利用实测土水特征曲线试验数据进行拟合参数的贝叶斯更新分析还不足。本文基于贝叶斯理论分析花岗岩残积土土水特征曲线拟合参数的不确定性,根据试验测得的土水特征曲线数据获得了Van Genuchten模型拟合参数的后验分布。采用马尔可夫链蒙特卡罗方法的延迟拒绝自适应算法进行参数后验分布抽样,分析土水特征曲线置信区间,对模型参数的不确定性进行分析。
1土水特征曲线
对于土水特征曲线的研究,学者们提出了多种不同的土水特征曲线模型用于预测基质吸力与含水率或饱和度的关系,土中的土水相互作用较为复杂,且多为经验模型。本文采用Van Genuchten[11]提出的土水特征曲线模型进行分析,Van Genuchten(VG)模型表达式为θw=θr+(θs-θr)S(1)
S=1[1+(aψ)n](1-n-1)(2)式中:θw为土体的体积含水率;θs为饱和含水率;θr为残余含水率;S为饱和度;ψ为土体的基质吸力;a、n为曲线拟合参数,a与进气值相关参数;n为当基质吸力超过进气值时土中水流出率相关参数。
2贝叶斯方法
贝叶斯理论非常适合应用分析岩土工程问题,尤其在只能获得有限数据的情况。该理论认为任一未知参数均可以看作成随机变量,且具有不确定性,可以用概率分布来描述。贝叶斯公式可以表示为p(ζ|D)=p(D|ζ)p(ζ)p(D)(3)式中:p(ζ)为参数先验概率;p(ζ|D)为似然函数,体现模型输出与观测数据的似然度;P(ζ|D)为参数后验分布;p(D)为概率密度函数归化常数;ζ是不确定输入参数矢量。
根据选定的土水特征曲线拟合模型,拟合参数的不确定性可以通过贝叶斯理论估计,将拟合参数看成随机变量ζ。考虑到模型自身和参数的不确定性以及观测误差,真实值与模型预测值之间存在差值,其可以用一个误差参数ε来定义,用ε来代表其不确定性。Sm=S(ζ)+ε(4)式中:Sm是测量饱和度;S(ζ)为计算模型的预测饱和度;ε代表模型误差和测量误差。
假设ε符合正态分布,则ε的概率密度函数为h(ε)=12πσεexp-(ε-με)22σ2ε(5)式中:με为ε均值,本文取με=0;σ2ε为ε方差。
假設拟合参数ζ=[a,n]满足已知的先验分布p(ζ),根据贝叶斯公式,则在数组D中的拟合参数更新后验分布可以表示为[1213]p(ζ|D)=
c0p(ζ)(2π)-N2σ-Nεexp-N2σ2εJg(ζ|D)(6)式中:c0为归化常数;N为测量记录点数;p(ζ)为模型参数的先验分布,代表主观判断;Jg(ζ|D)可以表示为拟合优度。Jg(ζ|D)=1NNn=1[Sm(i)-S(ψ;ζ)]2 (7)式中:Sm(i)第i个测量点的饱和度;S(ψ;ζ)相对应模型参数所得到饱和度输出值。
土水特征曲线拟合参数的最优值可以通过函数拟合优度最小的方法获得,也就是后验密度函数最大时,最优值所对应的误差方差等于拟合优度最小值,即2ε=minJg(ζ|D)=Jg(|D) (8)由于土水特征曲线拟合参数值具有非负性,选取拟合参数ζ的先验分布为对数分布[14]。假定拟合参数之间非相关,则参数的先验分布的表达式为p(ζ)=∏mi=112πζiσlnζiexp-12ln(ζi)-μlnζiσlnζi2(9)式中:m为随机变量的个数; μlnζi和 σlnζi分别为随机变量对数均值和标准差。σlnζi=ln1+σζiμζi2(10)
μlnζi=lnμζi-12σ2lnζi(11)3土水特征曲线试验数据
采用GEOExperts应力相关的土水特征曲线压力仪测得花岗岩残积土土样的土水特征曲线数据。该设备通过增加或减小基质吸力,实现土样的脱湿和吸湿过程,利用高进气值陶土板能够在空气和水之间起隔膜作用的特点,可测量不同吸力范围的土水特征曲线。试验土样样本采集于江西省赣州市于都县金桥村附近的崩岗区,其物理性质指标为:比重2.73、液限40.0%、塑限27.5%、塑性指数12.5、最大干密度1.76 g/cm3。将通过2 mm孔径筛的土样制成干密度为1.45、1.50、1.55、165 g/cm3的试样;将分别通过0.5、1、2 mm孔径筛的土样制成干密度为1.60 g/cm3试样,对不同干密度和不同颗粒粒径大小的试样进行土水特征曲线试验。本文使用数据来源于上述七个土样的土水特征曲线试验数据。试验均采用重塑真空抽气饱和土样,所有土样进行一次脱湿试验,基质吸力施加值为0、5、25、50、100、200、300、400 kPa。具体试验过程限于文章篇幅不再展开,试验所得的各土样饱和度与基质吸力关系数据如图1中数据点所示。
图1最优土水特征曲线与实测数据
Fig.1SWCC of optimal parameters and laboratory data4不确定性估计
基于Van Genuchten拟合模型和前述方法,选取上述花岗岩残积土土水特征试验所测数据点进行贝叶斯分析,所得的土水特征曲线模型拟合参数的最优值及相应的其他值如表1所示。最优值所对应的土水特征曲线及土水特征曲线测量数据点如图1所示。图2为土水特征曲线模型拟合参数a、n的后验分布,分布的峰值点对应值(=0.016 6,=1.296 7)即为参数a、n的最优值。表1模型拟合参数的后验分布统计值
Table 1Summary of statistics of posterior distributionsμaσa μn σn 2ε0.016 60.016 78×10-71.296 41.296 71.0×10-40.002 6图2参数的后验分布
Fig.2Posterior probability density5马尔可夫链蒙特卡罗方法
当给定先验分布时,参数可以通过贝叶斯理论进行更新,对于输入参数的后验分布通常不能取得理论值,这时,后验分布就需通过随机的方法产生随机样本。马尔可夫链蒙特卡罗抽样方法可以很好地解决这个问题,实现复杂模型贝叶斯公式的数值计算。MCMC方法的基本思想是建立一个进行抽样的马尔可夫链,并最终趋于一个稳定分析,通过马尔可夫链获得后验分布的随机样本,再利用蒙特卡罗法求相关值,如期望值、最大后验分布概率、置信区间等。这个方法目前常用于后验分布抽样,也可应用于非线性、参数高维、参数高度相关的模型分析,并可以获得足够多的样本[10,16],还并能有效处理大量的随机参数,且不依赖于先验分布。MCMC采用的算法有适应性Metropolis算法(Adapive metropolis)、延迟拒绝算法(Delayed rejection)、延迟拒绝适应性算法(delayed rejection adaptive metropolis algorithm, DRAM)等。本文采用延迟拒绝适应性算法(DRAM)[15],其稳定收敛速度快,适应用性强,即使目标分布偏离高斯分布很大时,DRAM也能够获得好的抽样结果,目前,该算法在岩土工程领域应用较少。DRAM 算法结合了延迟拒绝算法和适应性Mertopolis算法的优点,在抽样过程中根据前面所得的抽样结果不断更新提议协方差,使其不断逼近目标分布函数。 Ci=C0i≤i0
sdcov(ζ0,…,ζi-1)+sdδIdi>i0 (12)式中:C0为初始协方差;sd为取决于空间维数的缩放因子,sd=2.42d[17]; cov(ζ0,…,ζi-1)为样本协方差矩阵;Id代表d维单位矩阵;δ代表小常数,保证Ci为非奇异矩阵。
协方差矩阵表达式为cov(ζ0,…,ζk)=1k(ki=1ζiζTi-(k+1)kTk)(13)式中:k=1k+1ki=0ζi。
对于i>i0,将式(13)代入式(12),协方差满足递归方程,即Cn+1=n-1nCn+sdn(nn-1Tn-1-
(n+1)nTn+ζnζTn+εId)(14)提出初始参数值ζ0,如果ζ(1)i被接受,此次接受概率公式为α1(ζi-1,ζ(1)i)=min1,p(θ(1)i|D)q1(ζ(1)i,ζi-1)p(ζi-1|D)q1(ζi-1,ζ(1)i)(15)式中:q1为第1次形成的分布。
如果ζ(1)i被拒绝,根据当前值第2次迭代继续,提议第2次分布q2,其接受概率為α2(ζi-1,ζ(2)i)=min1,p(ζ(2)i|D)q1(ζ(2)i,ζ(1)i)q2(ζ(2)i,ζ(1)i,ζi-1)p(ζi-1|D)q1(ζi-1,ζ(1)i)q2(ζi-1,ζ(1)i,ζ(2)i)
×[1-α1(ζ(2)i,ζ(1)i)][1-α1(ζi-1,ζ(1)i)](16)式中:q2是第2次形成的分布。
这个程序可以不断地迭代进行,直至获得足够的抽样样本。
6置信区间分析
基于MCMC的土水特征曲线置信区间分析计算具体步骤:
1)确定土水特征曲线拟合参数向量ζ的先验分布p(ζ),假定随机变量的先验分布为独立对数分布,a均值和标准差分别为0.05和0.05;n均值和标准差分别为1.5和0.3;
2)根据土水特征曲线实测数据点确定似然函数p(D|ζ);
3)以后验概率密度函数P(ζ|D)为目标函数,采用延迟拒绝适应性算法获得随机样本;
4)删除收敛前的参数样本,将收敛后的样本作为后验概率密度函数的样本;
5)计算后验分布的置信区间。
考虑土水特征曲线拟合参数的不确定性,不同置信区间所对应的水土特征曲线和相应拟合参数可以用前述方法获得。通过MCMC方法,在分布空间取样,对样本点建立迭代条件,抽取收敛于后验分布函数的样本,获得符合Van Genuchten模型的20 000个土水特征曲线样本。图3为产生参数a、n随机变量样本的时程变化图。
图3随机样本的时程变化图
Fig.3Evolution processes of random samples去掉收敛前的3 000个样本,将剩余的17 000个样本作为后验分布样本,即生成了17 000组模型参数[a,n]。所以,对于一个给定的基质吸力,有17 000个相应的饱和度。通过对这17 000个饱和度重新排列,可以获得不同置信度的土水特征曲线和相关拟合参数。各置信度对应的拟合参数值如表2所示。土水特征曲线的拟合参数a的置信区间范围[0.009 3,0.036 1],n的置信区间范围[1.191 9,1447 2],所得的参数可用于分析非饱和土工程的可靠度分析。百分点可用来表征拟合参数的置信区间,如50%置信区间为[25百分点,75百分点],75%置信区间为[12.5百分点,87.5百分点]。不同置信区间对应的土水特征曲线如图4所示,图中给定了不同置信区间的上下限。表2不同置信度百分点的拟合参数值
Table 2Fitting parameter for different
percentiles of SWCC samples百分点an2.50.036 11.447 250.032 11.416 712.50.027 11.375 9250.022 61.334 7750.013 81.247 187.50.011 71.223 5950.010 31.203 097.50.009 31.191 9图4土水特征曲线的置信区间
Fig. 4Confidence intervals of SWCC7结论
根据贝叶斯理论框架,采用最大似然法,获得花岗岩残积土土水特征曲线的最优值。建立了基于延迟拒绝自适应(DRAM)算法的土水特征曲线参数估计方法,该算法具有很好的鲁棒性和灵活性。通过对模型参数后验分布抽样,采用后验分布的稳态随机样本可以对土水特征曲线的某一置信水平的区间进行预测。融合马尔可夫链蒙特卡罗方法为岩土工程中各类模型参数优选和不确定性分析提供有效手段。(致谢:感谢澳大利亚纽卡斯尔大学黄劲松教授对本文的指导和帮助。)
参考文献:
[1] ASSOULINE S. A model for soil relative hydraulic conductivity based on the water retention characteristic curve [J]. Water Resources Research, 2001, 37(2):265271.
[2] RAO B H, SINGH D N. Establishing soilwater characteristic curve of a finegrained soil from electrical measurements [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(5): 751754.
[3] FREDLUND M D, FREDLUND D G, WILSON G W. Prediction of the soilwater characteristic curve from grainsize distribution and volumemass properties [C]// 3rd Brazilian Symposium on Unsaturated Soils, Rio de Janeiro, Brazil, 1997: 1323.
[4] PHOON K K, SANTOSO A, CHENG Y G. Probabilistic analysis of soil water characteristic curves from sandy clay loam [C]// Proc.,GeoCongress 2008: The Challenge of Sustainability in the Geoenvironment, Geotechnical Special Publication, 2008,178: 917925.
[5] 谭晓慧,李丹,沈梦芬,等. 土水特征曲线参数的概率统计及敏感性分析[J]. 土木建筑与环境工程,2012,34(6):97103.
TAN X H, LI D, SHEN M F, et al. Probability statistics and sensitivity analysis of parameters of soilwater characteristic curves [J]. Journal of Civil, Architectural & Environmental Engineering, 2012,34(6):97103.(in Chinese)
[6] 徐全,谭晓慧,辛志宇,等. 土水特征曲线的概率分析[J].水文地质工程地质,2015,42(3):7985.
XU Q, TAN X H, XIN Z Y, et al. Probabilistic analysis of the soilwater characteristic curve [J]. Hydrogeology and Engineering Geology, 2015, 42(3):7985. (in Chinese)
[7] PHOON K K, SANTOSO A, QUEK S T. Probabilistic analysis of soilwater characteristic curves [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(3): 445455.
[8] WANG Y, AU S K, CAO Z J. Bayesian approach for probabilistic characterization of sand friction angles [J]. Engineering Geology, 2010, 114: 354363.
[9] 左自波,张璐璐,程 演,等. 基于MCMC 法的非饱和土渗流参数随机反分析 [J]. 岩土力學,2013,34(8):23932400.
ZUO Z B, ZHANG L L, CHENG Y, et al. Probabilistic back analysis of unsaturated soil seepage parameters based on Markov Chain Monte Carlo method [J].Rock and Soil Mechanics, 2013,34(8):23932400.(in Chinese)
[10] KELLY R, HUANG J. Bayesian updating for onedimensional consolidation measurements [J].Canadian Geotechnical Journal, 2015, 52: 13181330.
[11] VAN GENUCHTEN M T. A closedform equation for predicting the hydraulic conductivity of unsaturated soils [J].Soil Science Society of America Journal, 1980, 44:892898.
[12] YAN W M, YUEN K V, YOON G L. Bayesian probabilistic approach for the correlations of compression index for marine clays [J].Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135: 19321940.
[13] YUEN K V. Recent developments of Bayesian model class selection and applications in civil engineering [J]. Structural Safety, 2010, 32 :338346.
[14] HUANG J, GRIFFITHS D V, FENTON G A. System reliability of slopes by RFEM [J].Soils and Foundations, 2010, 50(3): 343353.
[15] HAARIO H, LAINE M, MIRA A, et al. DRAM: efficient adaptive MCMC [J]. Statistics and Computing, 2006, 16:339354.
[16] ZHANG L L, ZHANG J, ZHANG L M, et al. Back analysis of slope failure with Markov chain Monte Carlo simulation [J]. Computers and Geotechnics, 2010, 37: 905912.
[17] HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive metropolis algorithm [J]. Bernoulli, 2001, 7: 223242.
