基于非线性方程的多灰度失真图像拼接

(太原学院计算中心，山西 太原 030032)

0 引 言

多灰度光谱成像[1-2]具备能量集中、方向性好及高相干性的优点，能够显著提高图像的分辨率和清晰度[3-4]。图像重复性好、精度高、提取速度快，因此在医疗、救援、军事及缺陷检测等领域有着广泛而重要的应用[5-6]。由于光谱图像具有多灰度的特征，在成像的过程中由于设备故障、镜头抖动及受到外界环境的干扰会引起图像的失真；由于焦距校准和曝光量设置等人为因素同样也会造成图像的偏差[7-8]。多灰度图像的失真会给图像细节特征提取造成较大障碍，特别是一些重要的视频图像、监控图像，由于图像的失真会导致图像的失效，因此对多灰度失真图像的处理和拼接具有重要的意义[9-10]。

传统图像拼接算法设计，如基于矩阵的图像拼接系统设计[11-12]，通过对多灰度图像的匹配点间距离做最小化处理，采用目标函数来对失真的图像进行拼接，在对失真图像的拼接和重建过程中，由于受到图像灰度值变化的影响，反而增加了系统的误差、很难得到较好的图像失真度拼接效果[13-14]；双目立体图像拼接方法[15-16]，从单视点直接扩展到了多个视点，由于没有统一的基准图像，因此拼接效果不佳[17]。

1 多灰度失真图像拼接算法的设计

在对失真图像硬件系统构建的基础上，基于非线性方程设计失真图像拼接算法。首先调整参数，基于非线性方程对多灰度图像进行拼接。

设整个失真图像为平面内的一个有界区域，设其边界为T，其中(x,y)∈T，则失真图像的可用二元二阶非线性方程表示为：

(1)

在产生畸变和失真的图像上截取一条曲线段，选定6个目标点，然后采用相应的拼接模型系数进行相应的空间坐标转换，使其投射到目标图像上，利用投射到目标图像上点构成一条直线的约束条件，从而拟合出与位置相关的拼接模型系数的非直线方程。

令曲线上横轴上的坐标集合xi={x1,x2,……,x6}，纵轴的坐标集合为yi={y1,y2,……,y6}，其拼接系数为{k1,k2,…,k6}。设目标图像上的坐标为(x0,y0)，其横纵坐标的取样偏差可以分别表示为：

(2)

设点P(x,y)为多灰度失真图像上的任一点，点P(x,y)的映射点P′的坐标值可以表示为(x,y,z)，基于正交投影法，将图像上的点Pi，依次投影在拼接图像上，则投影坐标与原多灰度失真图像上的坐标关系可以表示为：

(3)

由公式(3)整理可得

(4)

设α和β分别为投影线与x轴和y轴的夹角，投影长度为l，原多灰度失真图像与转换后图像之间的坐标关系，可以描述为：

(5)

对公式(5)进行转化，求解出角度α和β，用公式表示为：

(6)

令拼接图像横轴和纵轴度数的取值范围为[0,180°]，那么α和β的横向线度数γ1和纵向线度数γ2可以分别表示为：

(7)

当失真多灰度图像拼接模型与拼接后目标图像的行的长度与列的长度都为2l时，目标图像上点P′(i,j)与横向线度数γ1及纵向线度数γ2的关系可以表示为：

(8)

畸变失真图像上坐标点与拼接后的目标图像上坐标点的对应关系可以表示为：

(9)

文章基于非线性方程原理，采用物像平面的坐标射算法，对多灰度失真图像的横、纵坐标做精确地转换，完成对失真图像坐标的拼接。

由于图像灰度变化较为强烈，同时受光通量、投影距离的大小等多方面因素，由于ITF 曲线一般为非线性的，可采用构建一种反函数，缓解灰度间的急剧变化，灰度响应曲线的反函数可以表示为：

G(x)=ζ·arctan(ξ·x·+τ)+χ

(10)

其中，G(x)表示拼接后输出的灰度值，ζ、ξ、τ、χ为系统经验参数，基于对经验参数的调整来实现对失真图像在灰度变化方法的拼接。

2 实验结果与分析

为验证提出基于非线性方程的多灰度失真图像拼接系统设计的有效性，本文从图像拼接后的垂直视差、图像拼接效果对比、及系统平均误差、最大误差对比等方面进行了仿真对比实验。

2.1 匹配点的精准度实验

在进行多灰度图像拼接之前，需要进行特征点的标记匹配，匹配精度决定了后期的拼接精度．匹配试验如图1所示。

图1 拼接之前的特征匹配试验结果

实验结果显示，图1为一幅多灰度失真图像，为了获得较好的失真图像特征匹配质量，依据图像各部分灰度的差异，将失真图像利用不同的能量进行灰度分割，通过能量的多次叠加得到灰度特征匹配图像，对比每一部分失真图像拼接前后的垂直视差，数据统计如表1所示。

从上图1和表1的数据对比可以分析出，在不同灰度的区域内，采用本文的方法进行多灰度失真图像特征匹配，能够较大幅度地降低图像的垂直视差，使图像的显示效果得以改善。

2.2 静态拼接试验1

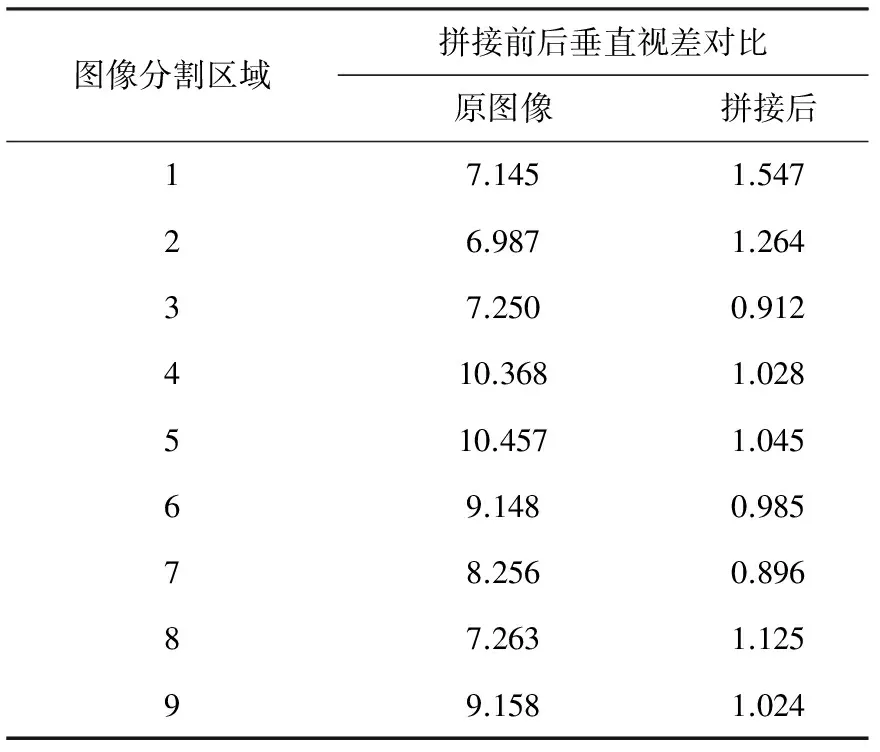
表1 多灰度失真图像拼接前后垂直视差对比

在多灰度失真图像的恢复效果对比方面，采用本文基于非线性方程的图像恢复系统设计，能够使失真的图像最大限度地恢复到原始状态，具有良好的图像拼接效果。

为了检验拼接图像的有效性，将其应用于一静态的汽车的失真图像为例，在拼接之前，首先对其进行特征匹配的试验如图2所示，而后进行对失真图像拼接，图中汽车和树木恢复前后结果对比分别如图3、图4所示。

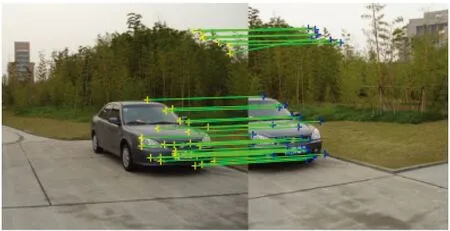
图2 拼接之前特征匹配试验结果

图3 拼接汽车图像前后效果对比

图4 拼接树木图像前后效果对比

可以看出，对失真图像拼接试验中，当目标汽车其背景为绿色树木，整个失真图像在拼接之前，呈现树木颜色过度集中单一，汽车棱角生硬，图像不存在立体感，颜色偏深，不能明显区分树木具体形态。而经过图像恢复系统进行了多灰度失真图像拼接后，汽车和树木原图像特征得到了恢复，整个图像画面的显示效果更加融合，树木呈现出立体的层次感，汽车的流体结构更加平滑，画面更加生动形象。

实验结果显示，通过本文方法对失真图像拼接，能够较好的恢复原图像的信息，消除图像失真。

2.3 动态拼接试验2

图像在进行拼接过程中，系统误差的控制情况直接影响图像的拼接效果，本文提到的基于非线性方程的多灰度图像恢复方法对于误差的控制快速稳定，误差较小且能够控制在一定范围之内，为了验证其控制的良好性能，将多灰度图像恢复方法应用在两辆正在移动的出租车上来做实验分析，对移动的汽车控制过程应用图像的70-72帧系统图像进行对比分析。两辆移动的汽车多灰度拼接图像如图5所示。

图5 对移动汽车拼接后的图像

图6 移动汽车70-72帧拼接图像

由图6系统图像可知，本文基于非线性方程的系统设计在失真图像拼接时的系统控制快速，平均误差稳定并且相对较小。

为了验证本文对图像恢复的控制有效性，分别统计传统基于系数矩阵的图像拼接系统设计和本文基于非线性方程的系统设计在失真图像拼接时的平均误差和最大误差，表2所示。

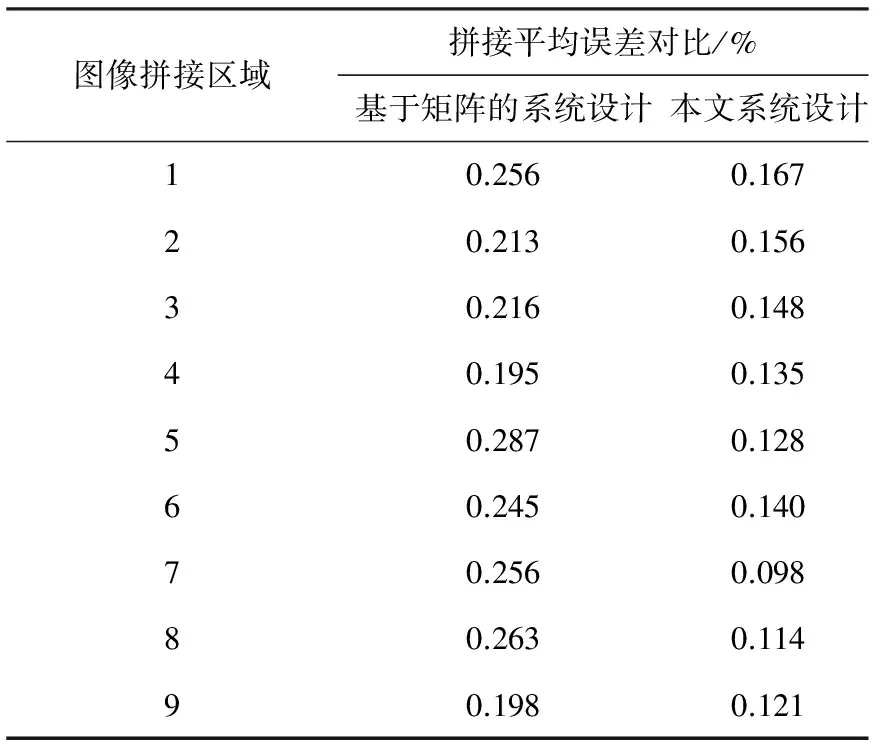
表2 两种图像拼接系统设计平均误差对比

由表2数据对比分析可知，传统基于系数矩阵的图像拼接系统控制的平均误差为0.237%，最大误差为0.287%，其误差相对较大，系统不稳定。而本文基于非线性方程的系统设计在失真图像拼接时的系统平均误差为0.134%，最大误差为0.167%，其误差相对稳定，波动小。

2.4 试验结果量化分析

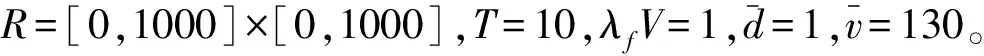
图7表明了多灰度失真图像数目K与标准化正确关联NCA之间的函数关系。从图7中可知，当多灰度失真图像数目K变大时，传统基于系数矩阵的图像拼接方法的执行效果将明显降低，也就是NCA急剧变小，并且当K≥30时，NCA小于0.5；而对于本文方法，当多灰度失真图像数目K变大时，拼接效果显然优于传统基于系数矩阵的图像拼接方法，因为NCA变化相对缓慢，当K≤50时，NCA大于0.8，并且在目标跟踪数目达到100时，NCA大于0.6。

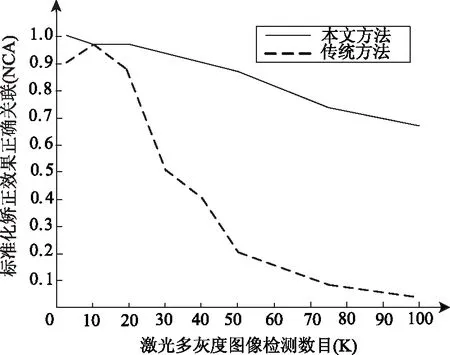
图7 多灰度图像拼接数目K与NCA函数关系

图8表明了多灰度失真图像数目K与ICAR之间的函数关系。从图中可看出，对于传统基于系数矩阵的图像拼接系统，随着多灰度失真图像数目K的增大，ICAR也逐渐上升，尤其是当多灰度失真图像数目K≥40时，ICAR急剧上升；而对于本文方法，随着多灰度失真图像数目K的增大，ICAR虽然有所增大，但是ICAR始终小于等于0.5。当K≤30时，传统方法与本文方法的执行效果相当，但是当K>30时，本文基于非线性方程的系统设计在失真图像拼接时误差概率要明显小于传统基于系数矩阵的图像拼接方法。

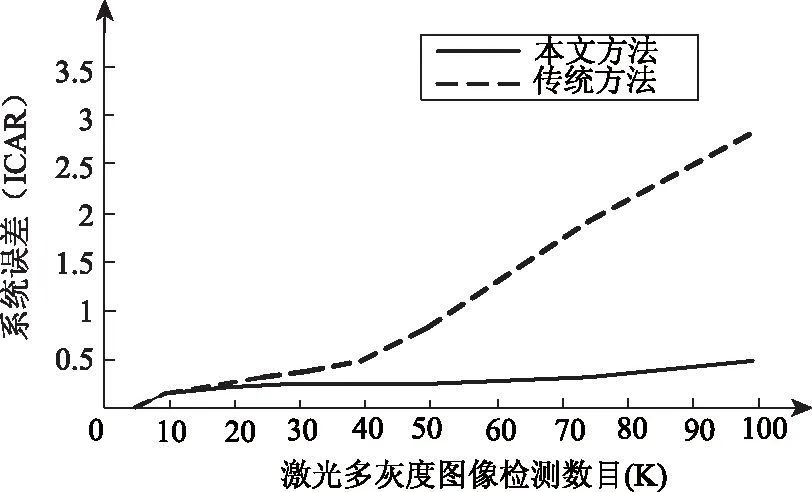
图8 多灰度图像拼接数目K与ICAR函数关系

3 结 语

针对现有失真图像拼接系统误差率高、非全局拼接的不足，本文提出了一种基于非线性方程多灰度失真图像拼接方法，依据像素失真后非线性变化的规律，设计了以图像解码模块和图像拼接模块为中心的失真图像拼接算法；采用物像平面的坐标映射算法，对多灰度失真图像的横、纵坐标做精确地转换，并依据灰度响应曲线的反函数，实现图像灰度失真的拼接，实验证明方法有效，但是本文方法在强干扰下，鲁棒性会大幅下降，这是需要进一步解决的问题。

[1] 张运海,杨皓旻,孔晨晖,等.激光扫描共聚焦光谱成像系统[J].光学精密工程,2014,22(6):1446-1453.

[2] 季云飞,耿林,冯国旭,等.激光成像技术的新发展[J].激光与红外,2015,24(12):1413-1417.

[3] 王雪培,赵虹霞,李青会,等.多光谱成像技术分析彩色艺术品的相关基础研究[J].光学学报,2015,35(10):304-311.

[4] 焦萌.调谐二极管激光吸收层析成像技术研究进展[J].激光杂志,2014，34(2):1-3.

[5] 徐奕奕, 刘智琦, 刘琦. 基于改进的分水岭算法图像分割方法研究[J]. 计算机仿真, 2011, 28(9):272-274.

[6] 陶荣华,陈标,赵海彬,等.高光谱遥感数据吸收位置特征融合提取技术研究[J].激光杂志,2013,29(5):27-28.

[7] 王玲玲,孙艳丽,王康.基于激光传感器的路径识别算法与实现[J].电子设计工程,2016,24(4):26-28.

[8] 海洁,吴海燕,罗中剑.高斯变邻域差分的灰度图像增强算法[J].激光杂志,2015,32(1):57-61.

[9] 胡维星,张海庄,彭阁鹏,等.激光光斑图像伪彩色处理方法研究[J].现代电子技术,2013,36(2):26-28.

[10] 王宇庆.基于图像结构信息复数表示与奇异值分解的灰度图像质量评价方法[J].光电子·激光,2012,20(9):1827-1834.

[11] 崔毅,危峻,黄小仙.基于线扩散函数矩阵的成像光谱仪图像矫正方法[J].红外技术,2014,36(2):115-119.

[12] 袁航飞, 郭永飞, 刘春香,等. 航天遥感相机星上自适应图像增强研究与实验[J]. 计算机测量与控制, 2014, 22(9):2962-2966.

[13] 李世成,娄磊,顾海明,等.高速图像运动分析中视差矫正方法研究[J].机械研究与应用,2014,36(1):79-81.

[14] 艾赛江,王翔.基于交比不变性的广角成像系统几何失真校正[J].中国激光,2012,21(1):186-193.

[15] 陈蓉,罗晓曙.一种基于双目立体视觉的图像校正算法设计[J].测控技术,2016,35(5):16-19.

[16] 王珊珊,邵枫,蒋刚毅,等.基于双目能量响应的无参考立体图像质量评价[J].光电子·激光,2014,23(4):741-747.

[17] 刘畅,李素梅.影响立体图像舒适度的对比度范围的测定[J].光电子·激光,2014,18(4):748-755.