基于多分辨率高斯滤波器组的时频分析方法
2017-03-28,,,
,, ,
(1.综合业务网络理论及关键技术国家重点实验室,西安电子科技大学,陕西 西安 710071;2.国网陕西省电力公司电力科学院研究所,陕西 西安 710048; 3.国网商洛供电公司,陕西 商洛 726000)
0 引 言
随着电气设备状态检修工作的深入开展,带电检测、在线监测等状态检测工作已经成为电力设备状态、隐患排查的重要支撑手段工作。高压电气设备(如变压器、封闭式组合电器等)在运行中,由于内部各种激励的作用会产生振动,当振动到达一定程度甚至会发出异响,电气设备的大量运行状态信息蕴含在音频信号中[1]。文献[2]指出变压器正常运行时可听声段频的基频为100 Hz,100 Hz的倍频分量200、300、400 Hz等成分比较丰富,呈线状频谱。通过对音频信号的时频分析,能够有效地对电气设备运行状态特征进行监测。
滤波器组分析法是一种传统的信号时频分析法,在语音识别、图像处理等领域被广泛应用。滤波器组的设计需要与待分析信号特征相吻合,如Gammatone滤波器组是根据人耳听觉模型特征设计的,对语音信号识别具有优良特性[3];小波变换实质上等效于一组不同频率特性的滤波器对信号进行滤波,能够对信号进行精细化时频分析[4]。
心理声学研究表明,人耳对声音信号的听觉感知以临界频带为基础,类似一组非等宽的子带滤波器组[5]。耳蜗基底膜具有良好的频率选择特征和频谱分析特征,能够将复杂声信号中不同频率成分映射为基底膜不同位置的振动,且在靠近耳蜗顶部的低频处,频率分辨率较高;而在靠近耳蜗底部的高频处,频率分辨率较低[6]。并且,基底膜的非线性特性是听觉系统具有抗干扰能力的重要原因之一,其频率特征从底部到顶部呈对数减小,其中底部频率最大,顶部频率最小[7,8]。
本文提出一种基于听觉模型的多分辨率高斯滤波器组对变压器机械缺陷产生的异常声音信号进行时频分析,提取正常状态与故障状态下声音信号滤波器组倒谱系数特征,并基于FCM-RBF神经网络进行故障诊断,丰富变压器故障诊断方法。
1 基于高斯滤波器组特征提取
多分辨率高斯滤波器组时频分析法属于一种“类小波变换”频谱分析法。其多分辨率特性借鉴于小波变换的多尺度分析特性与人耳听觉系统基底膜频率响应特性,即对于低频部分信号,具有较高的频率分辨率,反之,对高频部分信号具有较高的时间分辨率。同时N个滤波器中心频率仿人耳听觉系统模型呈非线性分布于20~20 kHz音频信号频带范围。
1.1 听觉模型的指数压缩
人体耳蜗对声音的识别过程本质在于其基底膜的分频效应。耳蜗在空间轴上相当于一组频率响应重叠的并联带通滤波器,串行时域语音信号经耳蜗处理即被分解为在不同的位置上具有不同频率特性的并行输出信号[9,10]。
从高频到低频依次K个中心频为:
(1)
式中,f0,c0由人为选定,c0>1用于调节频率变化规律。以音频信号(20~20 kHz)为例,当c0取不同值时各个中心频率分布规律如图1所示。显然,当c0取值过大时,信号低频带被“过度压缩”,对总频带进行了不合理划分。
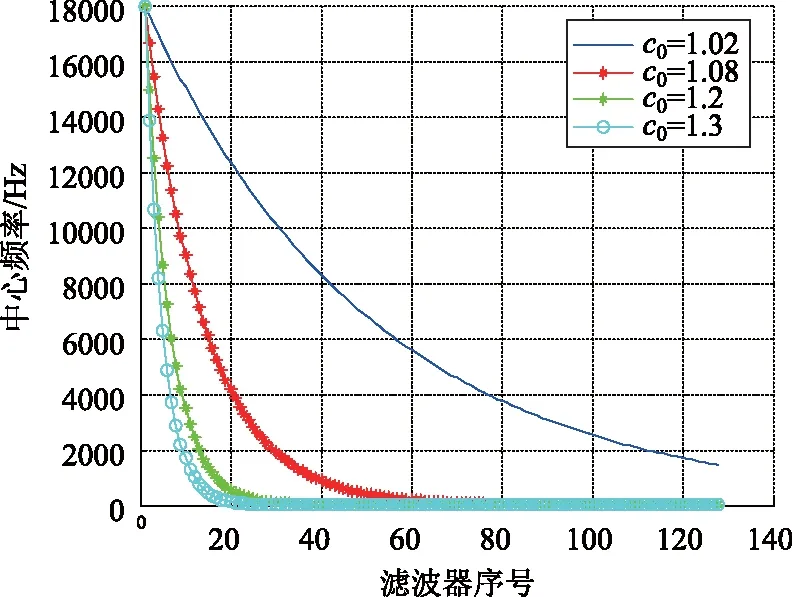
图1 滤波器中心频率随c0取值的变化情况
1.2 高斯小波滤波器组原理
信号x(t)的短时傅里叶变换(Short-time Fourier Transform, STFT)定义为:
(2)
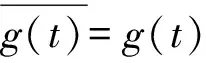
信号x(t)的小波变换定义为:
(3)
式中,a,b∈R,a≠0分别为尺度、位移因子。小波函数ψ(t)随着a的改变而进行伸展或压缩。
STFT的不足之处在于,截取信号的窗长是固定的,一旦选定窗函数,则对任何信号的时频分辨率都是确定的。小波变换的多尺度分析,克服了STFT单一分辨率的缺陷。
比较式(2)、(3),基于小波变换的时频多分辨率特性,将STFT进行扩展,设计一组具有不同时频分辨率特性的短时窗函数。
以音频信为例,取ε=2.5,c0=1.08,f0=18 kHz。设滤波器的个数K=32,则每个高斯滤波器的中心频率fk=18000/1.08k-1,滤波器扩展因子σk=0.0002×c0k-1,k=1,2,…,32。滤波器的频率分辨率随着信号频率的增大而呈非线性下降。
按上述仿听觉系统模型中心频率分布规律,设置K个对数分布规律的中心频率fCenter=[fC1,fC2,...,fCK],每个中心频率对应一次STFT。选取高斯函数为窗函数。
(4)
式中,σk∈R,σk≠0为滤波器扩展因子,决定了高斯窗平滑程度,如图2;高斯滤波器的时频宽积最小,既能减小信号的失真,又可以有效地选频衰减,是一种理想的滤波器[11,12]。且中心频率左右3σk宽度即占据了整个窗的99%以上。设置高斯窗实际长度为Lk=2×round(ε·a)+1,其中ε取值范围为(2,4),round(·)为四舍五入运算。

图2 不同σ下高斯函数平滑程度
1.3 临界带宽
人耳对两个频率及响度不同的声音具有听觉掩蔽效应,即响度较高的频率成分容易将响度较低的频率成分淹没,使人耳对后者不易察觉[13,14]。类似地,当使用滤波器组对信号进行频谱分析时,由于相邻两个滤波器的功率谱响应曲线有一定的重叠部分,当相邻滤波器的频窗重叠部分超过一定范围时,信号通过两个滤波器后的输出信号也会出现类似的“听觉掩蔽效应”。相邻滤波器交点频率由尺度因子σk和中心频率fk决定,如图3所示。
(5)
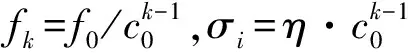
(6)
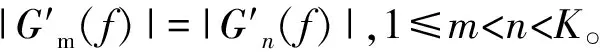
(7)
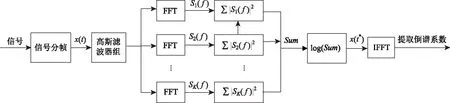
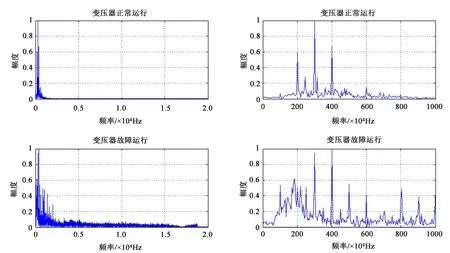
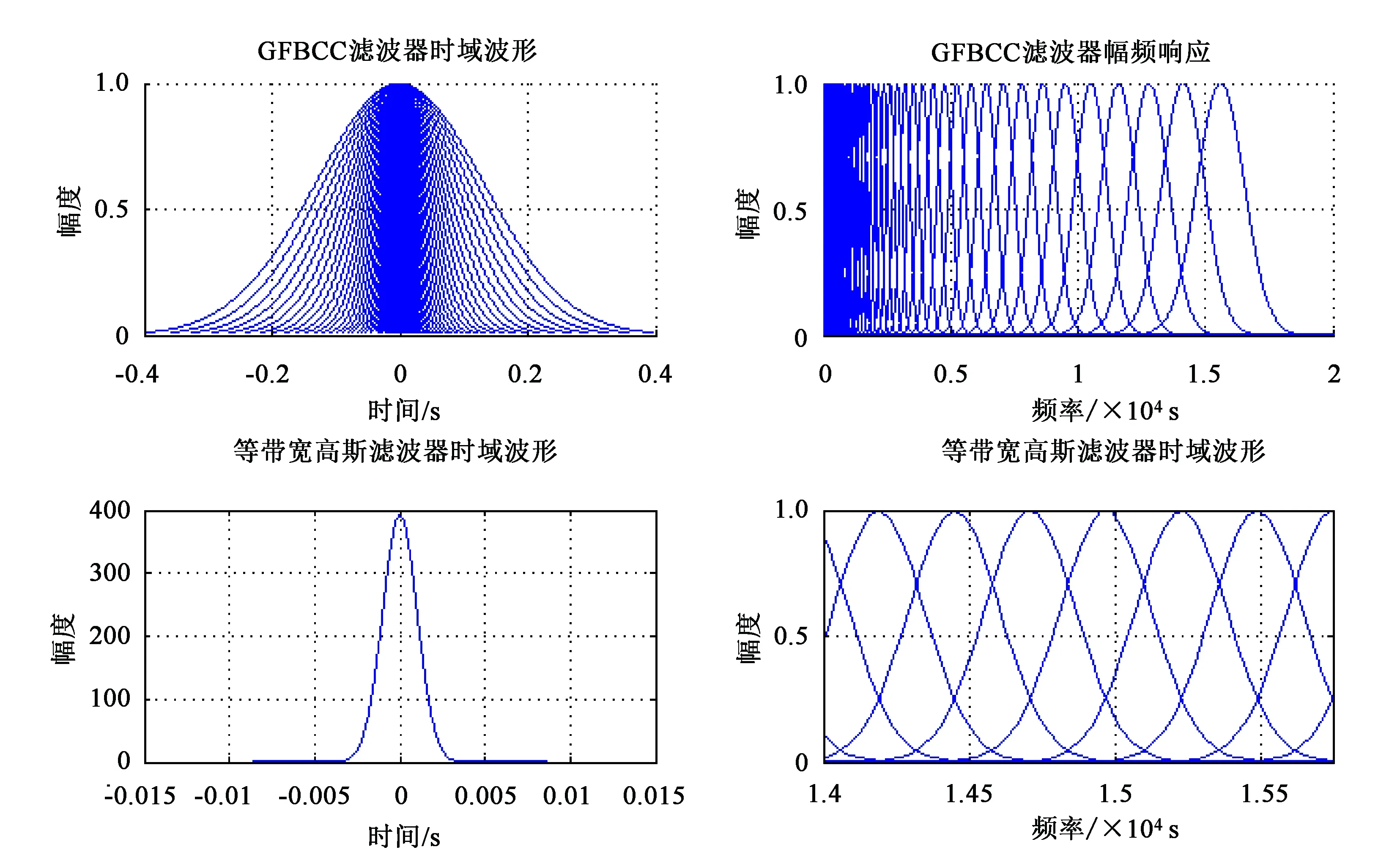
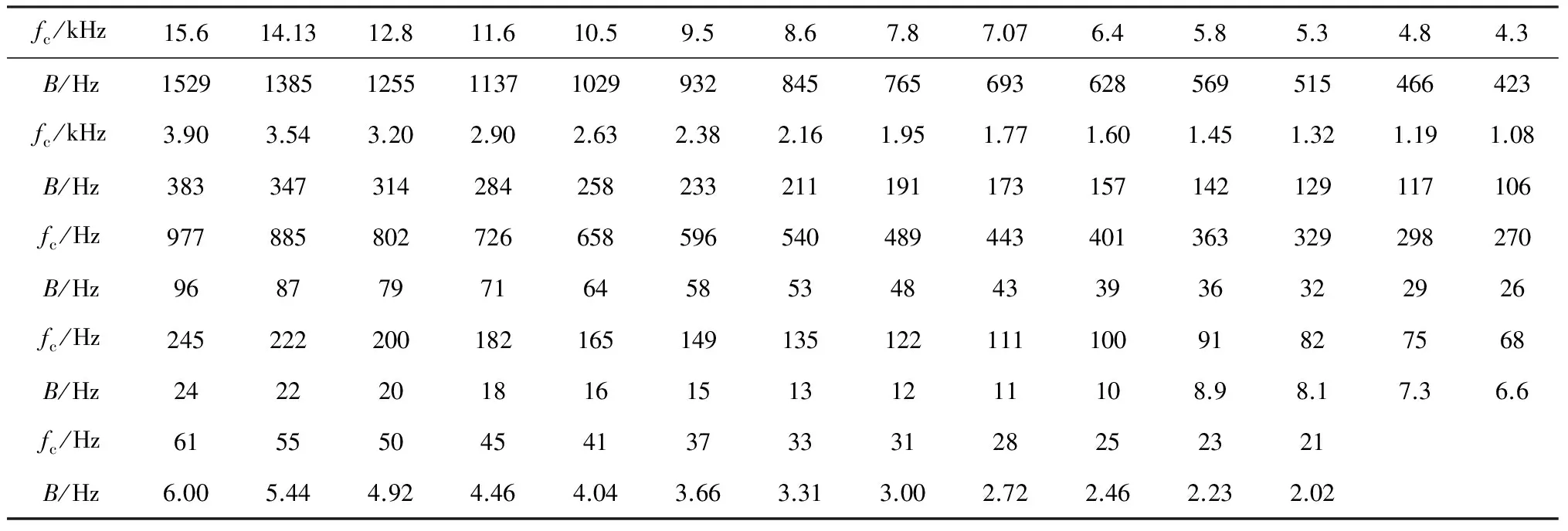
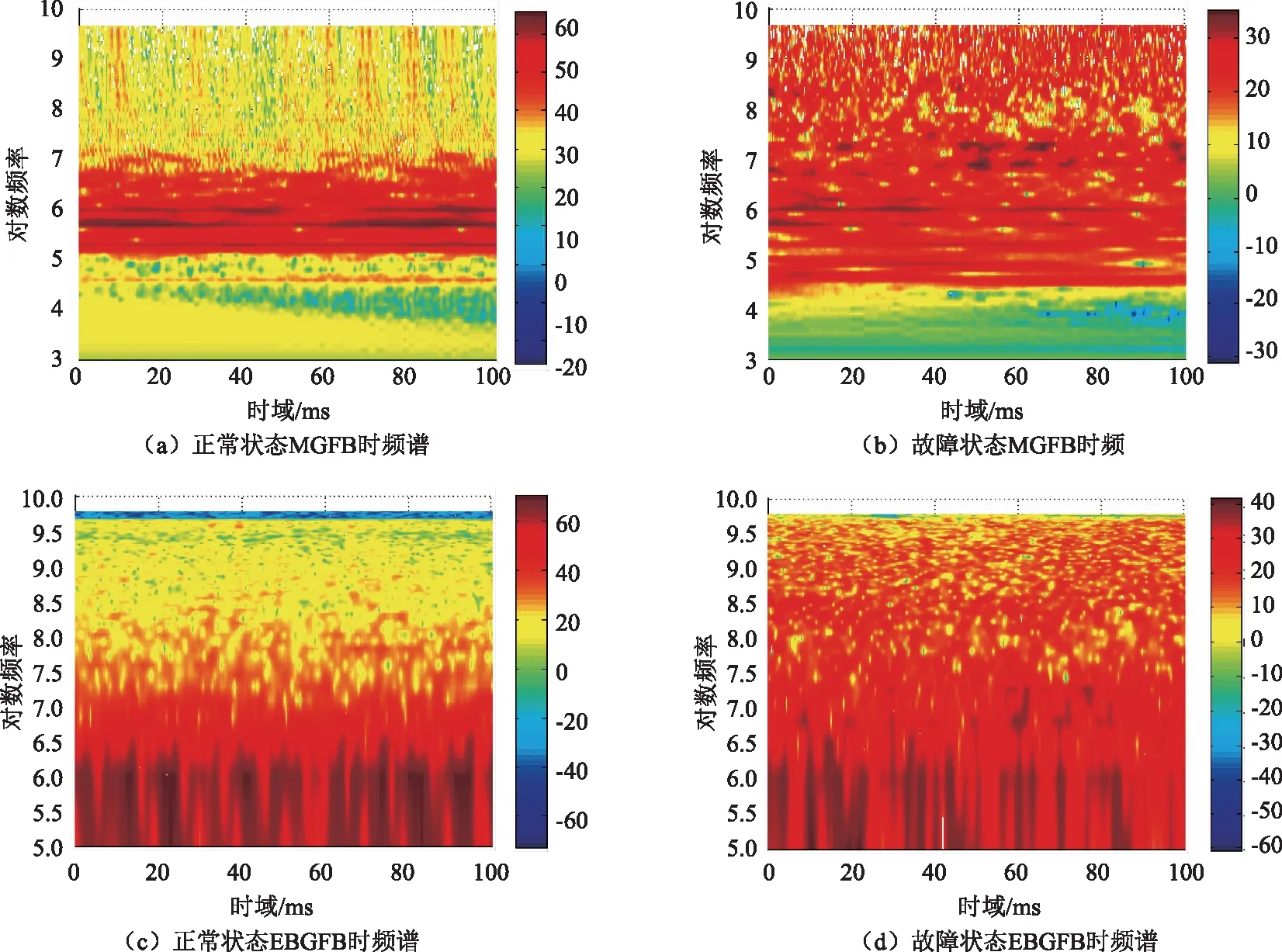
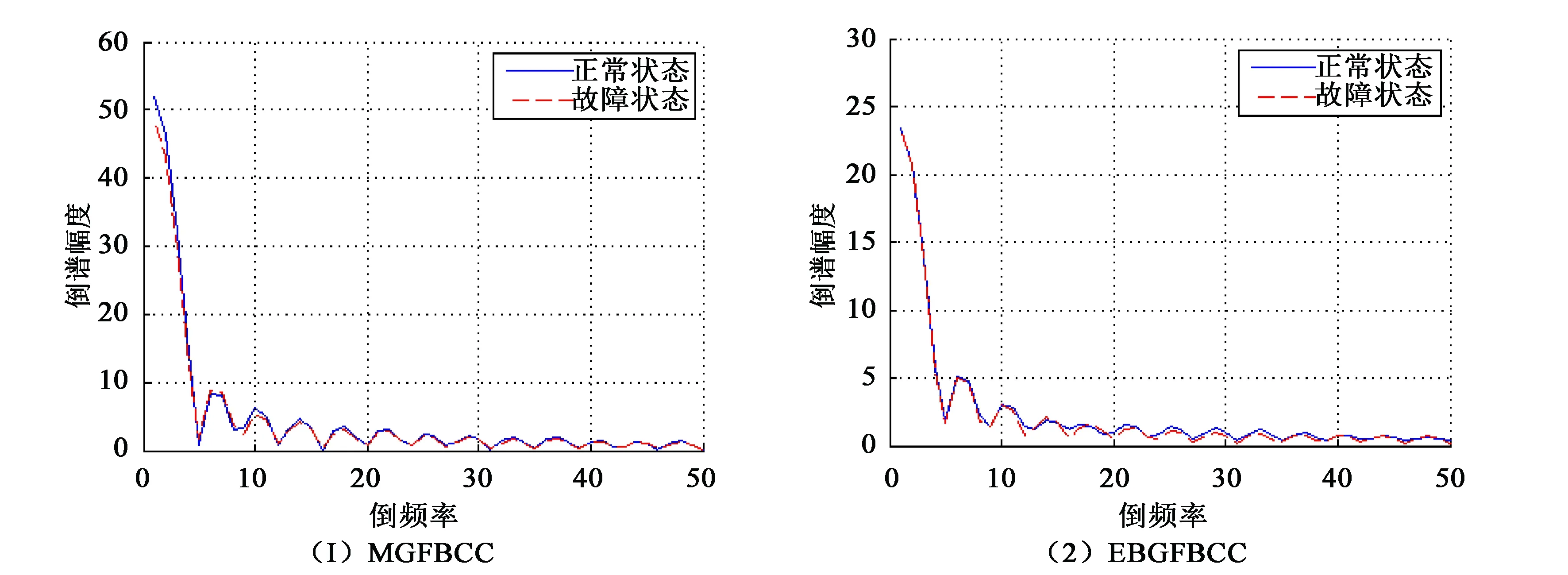
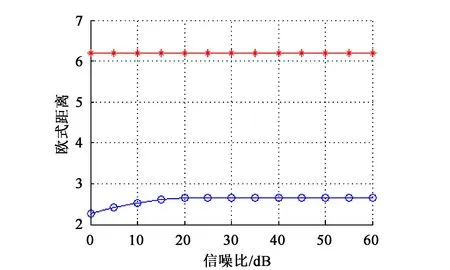
显然,fc2 (8) 式中,β=n-m,β∈[1,K-1],由式(8)得到如图4所示幅频响应曲线。显然,相邻两个滤波器间的频谱重叠为主要干扰。 图4 滤波器交点处幅频响应随c0变化情况 对于单个滤波器分析,其频率分辨率为Δfk=Bk,其中Bk为滤波器的-3 dB带宽。 (9) 由式(9)、(10)可知,参数c0和η同时决定着滤波器组的“掩蔽效应”、信号频带的划分及滤波器的时频分辨率。合理地选择c0和η的取值范围既能够利用滤波器组对所需分析的频段进行合理划分,又可以减小相邻滤波器频窗重叠部分的“掩蔽效应”的影响,提高时频分辨率。 (10) 本文通过小波变换多尺度分析及听觉系统特性,从STFT时频分析法出发设计多分辨率高斯滤波器组,同时采用对数变化的中心频率来模仿人耳听觉系统的非线性特性,提出一种基于多分辨率高斯滤波器组的电气设备音频信号的倒谱特征参数,记为MGFBCC(Multi-resolution Gauss Filter Bank Cepstrum Coefficient)提取算法。 图5 GFBCC提取流程 如图5所示,MGFBCC特征参数提取步骤如下: (1)本文设计的多分辨率高斯滤波组参数可根据待分析的信号频谱特征进行设计。首先对信号进行频谱分析,根据信号频谱初步分析结果及信号频带范围确定滤波器个数、中心频率变化规律及滤波器的时频分辨率,即设计特征设计参数c0和η。基本原则为:①所有滤波器中心频率较好地对信号频带进行合理划分,信号能量集中频带需分布较多滤波器;②滤波器组的等效频率分辨率近似等于单个滤波器的-3 dB带宽;③信号高频部分具有高时间分辨率和低频率分辨率,而低频部分具有高频率分辨率和低时间分辨率。 (2)原始信号经过滤波器组后得到一组滤波后的子带信号,对每个子带信号进行FFT并对离散功率谱进行求和,计算能量; (3)对步骤(2)中得到的能量特征向量取对数,得到一组对数能量谱。插零后再经过IFFT变换到倒频谱域,得到MGFBCC参数。 高压变电站中电气设备(如变压器、GIS等)在运行过程中会伴随着音频机械振动及异响信号。本文基于国网陕西省电科院提供的西安某地变压器正常运行及故障运行时的声音信号,设计两组高斯带通滤波器组进行时频分析,一组为上述多分辨率高斯带通滤波器组,提取MGFBCC特征参数;另一组为等带宽高斯带通滤波器,用于提取EBGFBCC(Equal Bandwidth Gauss Filter Bank Cepstrum Coefficient)特征参数。同时,将两组特征参数进行模糊C均值聚类分析,并设计RBF神经网络进行故障识别。实验分析比较了两组高斯带通滤波器组的时频分析性能及特征参数故障识别率。 2.1.1 MGFB参数设计 如图6所示为变压器处于正常运行时和故障状态下发出的声音信号归一化频谱。显然,声音信号主要能量集中在低频段(2000 Hz以内)。此外,在频率为200 Hz、300 H、400 Hz等谐波分量具有主导能量集中。并且正常状态与故障状态下,工频谐波能量分布情况差异明显。 综上,根据图7所示信号频谱特征设计滤波器需满足如下条件: ▶ 低频部分滤波器的频率分辨率较高,反之高频部分的频率分辨率较低。 ▶ 滤波器中心频率应包含200 Hz、300 Hz、400 Hz 等几个重要频率工频谐波分量。 经多次实验后,对20~20 kHz音频范围设计了68个滤波器。如图7所示,相邻滤波器的频窗交点处的幅度衰减约为0.707,能够较好地抑制滤波器“掩蔽效应”,另外,滤波器的参数c0=1.104,f0=16500,η=0.000173,则MGFB的中心频率fc及带宽B如表1所示。可以看出MGFB中心频率与信号频谱相吻合,最大的时间分辨率和频率分辨率分别约0.1 ms和2.02 Hz。 图6 变压器声音信号归一化频谱 图7 高斯带通滤波器组幅频响应 2.1.2 EBGFB参数设计 如图7所示,EBGFB滤波器组中心频率由式(11)给出,呈线性分布。各个滤波器时频分辨率均相同,分别为3.85 ms和260 Hz。相邻滤波器幅频响应曲线交点处幅频响应约为0.707,符合滤波器组设计原则。 (11) 2.1.3 MGFB与EBGFB性能比较 待分析声音信号采样率为44.1 kHz,则故障诊断实验步骤为: ①综上提取声音信号两组N×M维特征矩阵FMGFBCC和FEBGFBCC分别训练RBF神经网络,其中N,M分别为特征总数及特征向量维数; ②将总的样本特征矩阵分为N1个训练特征TrN1×M和N2个测试特征TeN2×M; ③对TrN1×M进行模糊C-均值聚类得到C个聚 ④ 将TeN2×M输入训练好的RBF神经网络,进行故障诊断,并统计正确诊断概率。 表1 MGFB中心频率和等效带宽对应关系 表2 EBGFB中心频率和等效带宽对应关系 2.2.1 时频分析性能比较 基于MGFB与EBGFB对信号进行时频分析,信号经滤波后的时频谱如图8所示。 分别比较(A)和(C),(B)和(D),由于EBGFB的恒定窗宽所致时频分辨率的单一性,滤波器时频分辨率对于信号低频部分及高频部分不能很好地适应,无法对信号时频域方向上进行自适应地描述。(A)和(B)中,MGFB时频谱具有更丰富的信号时频特征信息:在低频部分MGFB具有较高的频率分辨率,可以清晰看出在中心频率为200Hz、300Hz及400Hz等谐波频点处始终具有较大的能量集中;在高频部分,MGFB时频图具有较高的时间分辨率,能够看出信号高频成分在时间轴上的变化细节。 MGFB的多分辨率特性与小波变换及听觉模型中耳蜗基底膜的多分辨率特性均相吻合。 基于听觉模型及小波变换的多分辨率特性,使得MGFB相比于EBGFB时频谱能够更好地刻画信号高低频部分的细节特征。 2.2.2 故障诊断性能分析 变压器处于正常状态及故障状态下声音信号的倒谱系数如图9所示。 图8 变压器正常与故障状态下声音信号时频谱 图9 变压器正常与故障状态下声音信号倒谱系数 图10 变压器正常与故障状态特征向量稳定性 实验中选取前16个倒谱系数组成特征向量,共提取了正常状态及故障状态下声音信号共200个倒谱系数特征向量。其中100个作为训练特征向量,剩余100个作为测试特征向量,进行故障诊断实验。 经故障诊断实验得出,基于滤波器组倒谱系数特征具有很高的稳定性,如图10所示。在不同信噪比下,变压器处于故障状态及正常状态下声音信号的MGFBCC特征向量的平均欧式距离相比EBGFBCC 特征向量具有更高的可分性,并且具有更高的鲁棒性。 本文提出了一种基于人耳听觉系统模型及小波变换多尺度分析特性的多分辨率高斯带通滤波器组时频分析方法。详细分析了MGFB的相邻滤波器的“掩蔽效应”、等效带宽及时频分辨率,给出了滤波器组参数设计方法。同时,设计了一组等带宽高斯带通滤波器组进行性能比较。实验证明,本文提出的MGFB对变压器等电气设备声音信号具有良好的时频分析能力,能够自适应地刻画信号不同频率成分时频谱细节特征;此外,基于MGFB提取的倒谱系数MGFBCC对变压器故障诊断具有较好的性能。 [1] 周晓峰.机械振动源的分离和识别方法研究[D].浙江大学,2012. ZHOU Xiaofeng.Study on Separation and Identification of the Vibration Sources of Mechanical System[D].Zhejiang University,2012. [2] 杜一明.基于声信号的变压器故障诊断系统研究[D].华中科技大学.2013. Du Yiming.Research on Fault Diagnosis System for Power Transformer Based on Audio Signal[D].Huazhong University of Science & Technology.2013. [3] 胡峰松,曹孝玉.基于Gammatone滤波器组的听觉特征提取[J].计算机工程,2012,38(21). HU Fengsong,CAO Xiaoyu.Auditory Feature Extraction Based on Gammatone Filter Bank[J].Computer Engineering,2012,38(21). [4] 衡彤.小波分析及其应用研究[D].四川大学,2003. HENG Tong.Wavelet Analysis and its Application[D].Sichuan University,2003. [5] 廖启鹏.基于Gammatone听觉滤波器组和复倒谱盲解卷积的语音去混响研究[D].苏州大学.2012. Liao Qipeng.Speech dereverberation based on Gammatone auditory filter bank and inverse filter by complex cepstrum[D].Suzhou University.2012. [6] 陈世雄,宫琴.常见的听觉滤波器[J].北京生物医学工程,2008,27(1):94-99. Chen Shixiogn,Gong Qin.A review of auditory fliter[J].Department of Biomedical Engineering.2008,27(1):94-99. [7] 李勇军.基于听觉模型和置信机器的语音信号处理研究[D].湖南大学.2014. Li Yongjun.Research on Speech Signal Processing Based on Auditory Model and Transductive Confidence Machine [D].Hunan University.2014. [8] Du Weilin,Li Bin.Multi-strategy Ensemble Particle Swarm Optimization for Dynamic Optimization [J].Information Sciences,2008,178(15):3096-3109. [9] 高印寒,谢军,梁杰,李强.基于小波分析的听觉滤波器组模型[J].吉林大学学报(工学版),2008,38(Sup). GAO Yinhan,XIE Jun,LIANG Jie,LI Qiang.Auditory filter bank model based on wavelet transform[J].Journal of Jilin University(Engineering and Technology Edition),2008,38(Sup). [10] 周强.多频带非线性分析与感知多谱熵的声带疾病嗓音识别[D].苏州大学,2013. ZHOU Qiang.Vocal Cords Diseases Detection by Multi-band Nonlinear Analysis and Perception Polyspectra Entropy[D].Suzhou University,2013. [11] 孙颖,张雪英.基于高斯小波滤波器的语音识别特征提取方法[J].太原理工大学学报,2007,38(2):146-149. Sun Ying,Zhang Xueying.A Feature Extraction Method Based on Gauss Wavelet Filter in Speech Recognition[J].Journal of Taiyuan University of Technology. 2007,38(2):146-149. [12] 许景波.高斯滤波器逼近理论与应用研究[D].哈尔滨工业大学,2007. XU Jingbo.Study on Approximation Theory and Application of Gaussian Filter[D].Harbin Institute of Technology,2007. [13] 武方.基于人耳听觉系统模型的多声源定位与语音分离研究[D].河北工业大学,2009. Wu Fang.The Research of Multi Sound Sources Localization and Speech Separation Based on the Model of Human Auditory System[D].Hebei University of Technology,2009. [14] 王玥,李平,崔杰.听觉频域掩蔽效应的自适应β阶贝叶斯感知估计语音增强算法[J].声学学报.2013,38(4):501-508. Wang Yue,Li Ping,Cui Jie.Adaptive β-order perceptually motivated speech enhancement algorithm bansed on frequency-domain auditory masking[J].ACTA ACUSTICA.2013,38(4):501-508.
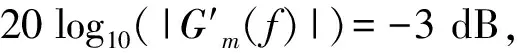
1.4 特征提取过程
2 实例分析
2.1 滤波器组参数设计
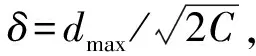

2.2 故障诊断实验结果
3 结 语
