（2+1）维类浅水波方程的有理解

嵇纯德

摘 要：通過广义双线性衍生方程 ， ，推导出广义双线性的（2+1）维类浅水波方程。基于非线性发展方程的双线性形式，可以通过符号计算直接获得方程的有理解。对（2+1）维类浅水波方程进行多项式求解得到方程了九类有理解。这些有理解可以描述一类代数孤立波，因此它们对于研究发生在海洋和大气中的孤立波具有很高的应用价值。此外，给出了特定参数的有理解三维图，用来描述能量分布。

关键词：有理解；广义双线性方法；（2+1）维类浅水波方程

DOI：10.16640/j.cnki.37-1222/t.2017.04.195

1 引言

众所周知，在物理学等科学学科中，非线性发展方程被广泛用来描述自然现象[1][2][3]。所以，例如有理解、代数几何解等非线性发展方程的解的问题成为了当今研究关注的焦点。以有理解为研究方向的课题在气象学和物理海洋学领域扮演着举足轻重的角色，例如怪波解是一类特殊的有理解，而怪波解能够描述海洋学[4][5]和非线性光学[6][7]中非线性波的现象。所以，研究非线性发展方程的有理解是非常有研究意义和价值的。

可积方程的有理解可以通过诸如达布变换[8]，双线性方法[9][10]等许多途径求得。可积方程包括Korteweg-de Vries方程（KdV方程）[8]，Boussinesq方程[11]，Toda晶格方程[12]，AB系统[13]，类KdV方程[14]，类Boussinesq方程[15]等等。另一方面，（3+1）维不可积KP I方程[16][17]和（3+1）维不可积KP II方程[12]的有理解也可以通过不同的方法求的。特别的，（3+1）维不可积KP II方程的有理解可以转化成 Boussinesq方程的有理解[12]。

研究过程主要是基于广义双线性形式得到一个（2+1）维类浅水波方程并由多项式解求得此类方程的有理解。论文主要包含对（2+1）维类浅水波方程的介绍，给出了（2+1）维类浅水波方程的有理解，最后比较了有理解的图像并进行了分析。

2 （2+1）维类浅水波方程及其广义双线性形式

4 总结

通过广义双线性方法讨论了（2+1）维类浅水波方程，并利用多项式函数求解（2+1）维类浅水波方程，从而获得了九类不同的有理解。研究过程中用到的基本理论是广义双线性算子[18]。

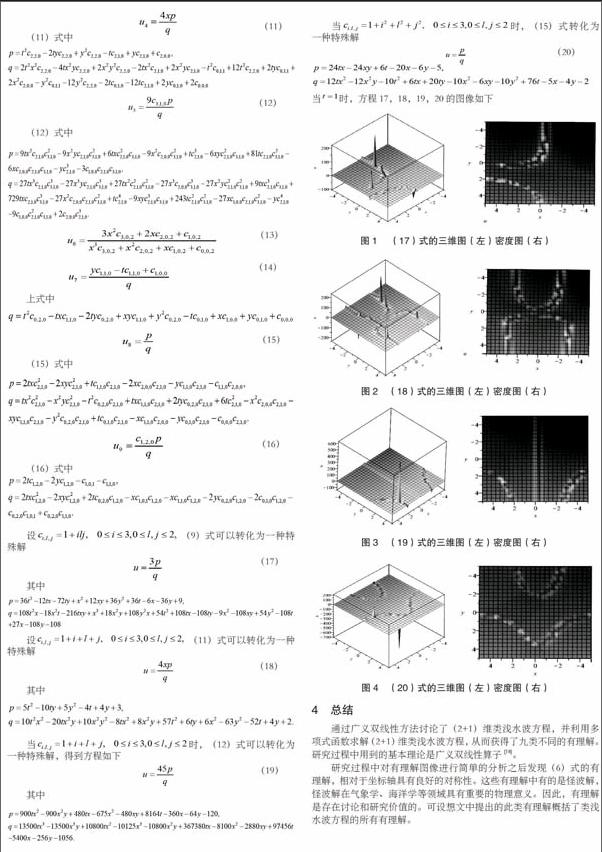
研究过程中对有理解图像进行简单的分析之后发现（6）式的有理解，相对于坐标轴具有良好的对称性。这些有理解中有的是怪波解，怪波解在气象学、海洋学等领域具有重要的物理意义。因此，有理解是存在讨论和研究价值的。可设想文中提出的此类有理解概括了类浅水波方程的所有有理解。

在研究过程中，通过同样的方法还得到了（3+1）维类浅水波方程的有理解，但（3+1）维方程的有理解与文中得到的（2+1）维方程的有理解是类似的，所以在此文中暂不讨论（3+1）维类浅水波方程。此外，文中对有理解的求解的过程对讨论类浅水波方波的Wronskian行列式解[19]Pfaffian解是非常有意义的。最重要的是，通过本文的研究可以向大家证明高阶微分方程的有理解是非常有研究价值的。

参考文献：

[1]Rogers C， Shadwick W F. Backlund Transformations and Their Applications[J]. 1982.

[2]Miura R M. B?cklund transformations， the inverse scattering method， solitons， and their applications ：[M]. Springer-Verlag， 1976.

[3]Yang H W， Yin B S， Shi Y L. Forced dissipative Boussinesq equation for solitary waves excited by unstable topography[J]. Nonlinear Dynamics， 2012， 70（2）：1389-1396.

[3]Müller P， Garrett C， Osborne A. Rogue waves-The Fourteenth ‘Aha Hulikoa Hawaiian Winter Workshop[J]. Oceanography， 2005， 18（3）：66-75.

[4]Kharif C， Pelinovsky E， Slunyaev A. Rogue waves in the ocean： observations， theories and modelling[J]. Investig Andin， 2008， 16.

[5]Solli D R， Ropers C， Koonath P， et al. Optical rogue waves.[J]. Nature， 2007， 450（7172）：1054-7.

[6]Akhmediev N， Dudley J M， Solli D R， et al. Recent progress in investigating optical rogue waves[J]. Journal of Optics， 2013， 15（6）.

[7]Ma W X， You Y. Solving the Korteweg-de Vries equation by its bilinear form： Wronskian solutions[J]. Transactions of the American Mathematical Society， 2005， 357（5）：1753-1778.

Ma W X， Li C X， He J. A second Wronskian formulation of the Boussinesq equation[J]. Nonlinear Analysis， 2009， 70（12）：4245-4258.

[8]Ma W X， You Y. Rational solutions of the Toda lattice equation in Casoratian form[J]. Chaos Solitons & Fractals， 2004， 22（2）：395-406.

[9]Tacchella A. On rational solutions of multicomponent and matrix KP hierarchies[J]. Journal of Geometry & Physics， 2010， 61（8）：1319–1328.

[10]Ma W X. Comment on the 3+1 dimensional Kadomtsev–Petviashvili equations[J]. Communications in Nonlinear Science & Numerical Simulation， 2011， 16（7）：2663-2666.

[11]Wang X， Li Y， Chen Y. Rogue wave solutions in AB system[J]. Communications in Nonlinear Science & Numerical Simulation， 2013， 20（2）.

[12]Ma W X. Bilinear equations， Bell polynomials and linear superposition principle[C]// 2013：594-597.＼

[13]Zheng H C， Ma W X， Gu X. Hirota bilinear equations with linear subspaces of hyperbolic and trigonometric function solutions[J]. Applied Mathematics & Computation， 2013， 220（4）：226-234.

[14]Khalfallah M. New exact traveling wave solutions of the （3 + 1） dimensional Kadomtsev–Petviashvili （KP） equation[J]. Communications in Nonlinear Science & Numerical Simulation， 2009， 14（4）：1169-1175.

[15]Sinelshchikov D I. Comment on： New exact traveling wave solutions of the （3+1）-dimensional Kadomtsev–Petviashvili （KP） equation[J]. Communications in Nonlinear Science & Numerical Simulation， 2010， 15（11）：3235-3236.

Ma W X. Trilinear equations， Bell polynomials， and resonant solutions[J]. Frontiers of Mathematics in China， 2013， 8（5）：1139-1156.

Ma W X. Wronskians， generalized Wronskians and solutions to the Korteweg–de Vries equation[J]. Chaos Solitons & Fractals， 2003， 19（1）：163-170.