基于低秩张量分解的大规模MIMO信息检测算法研究

刘星月, 周小平, 李 莉, 彭张节

(上海师范大学 信息与机电工程学院,上海 200234)

基于低秩张量分解的大规模MIMO信息检测算法研究

刘星月, 周小平, 李 莉, 彭张节

(上海师范大学 信息与机电工程学院,上海 200234)

提出了一种改进的Tucker分解法,将二维的张量分解到两个维度中.分别通过改进Tucker和Tucker算法的矩阵减秩和收敛运算,得到保存完整信息的原张量的近似估计值.仿真实验结果表明,改进Tucker算法提高了系统的检测性能.

大规模MIMO; 张量分解; 数据检测; Tucker算法

0 引 言

大规模MIMO通过在发送端和接收端使用大量的天线改善分集增益和信道鲁棒性,从而很大程度上提高了信道容量,因此在通信领域中得到广泛使用.在大规模MIMO的上行链路中,用户到基站的数据流在被接收器接收后,要进行解码处理,解码器会分辨出来自于不同用户的数据信息.

大规模MIMO天线可以利用三维信道信息实现更精准的波束赋形,支持更多用户和更多流传输,自适应波束赋形与跟踪,文献[1-2]提出了大规模MIMO的一般模型和各种参数,给出大规模MIMO收发端数据干扰模型,由于大规模MIMO的信息传播环境的特殊性,信号在传播过程中除了自身能量不断衰减外,遇到障碍物还会发生散射、反射和衍射,到达接收端时,多天线间和多用户间干扰会严重影响自适应波束赋形与跟踪.为了解决这个问题,文献[3-4]和[6-8]引入张量模型,针对低秩张量算法的模型进行了分解,将有利于分解信号干扰分量.文献[8]提出了Tucker低秩张量分解法,该方法将因子矩阵以一个核心矩阵为关联,表示大规模MIMO信道收发的两个维度数据的相关程度,剩余的数据主成分仍然保留在各维度的因子矩阵中,该方法存在的问题是Tucker分解后的每个因子矩阵的最佳逼近值还有待改善,大规模MIMO接收信息的准确度可以进一步提高.可以将核心矩阵进一步分解,增加一个核心矩阵,将原来Tucker分解法中的一个核心矩阵分解为两个核心矩阵从而提高接收信息的准确度.本文提出了一种改进的Tucker分解法,大规模MIMO无线信道看作一个二维张量来搭建信道模型,将二维的张量分解到两个维度中.将Tucker分解法进行改进,是为了进一步提高分解模型与原张量的接近程度,最大程度的保存原信息.分别通过改进Tucker和Tucker算法的矩阵减秩和收敛运算,对该模型进行张量分解并通过算法的迭代得到误差较小的信息矩阵,得到保存完整信息的原张量的近似估计值.

文章一共分为5个部分.第一个部分是关于大规模MIMO的空间模型介绍,分析了信道中信息数据由于传播中的损失导致信息的错误.第二部分是关于大规模MIMO张量分解,分析了张量分解的原理和分解方法.第三部分是张量分解法Tucker和本文作者提出的改进的Tucker分解法,说明了两种分解方法的分解原理,在这两种分解方法下数据检测的原理.第四部分对两种分解方法进行了仿真,比较了两种方法的误码率.最后一部分进行总结与展望.

1 系统模型

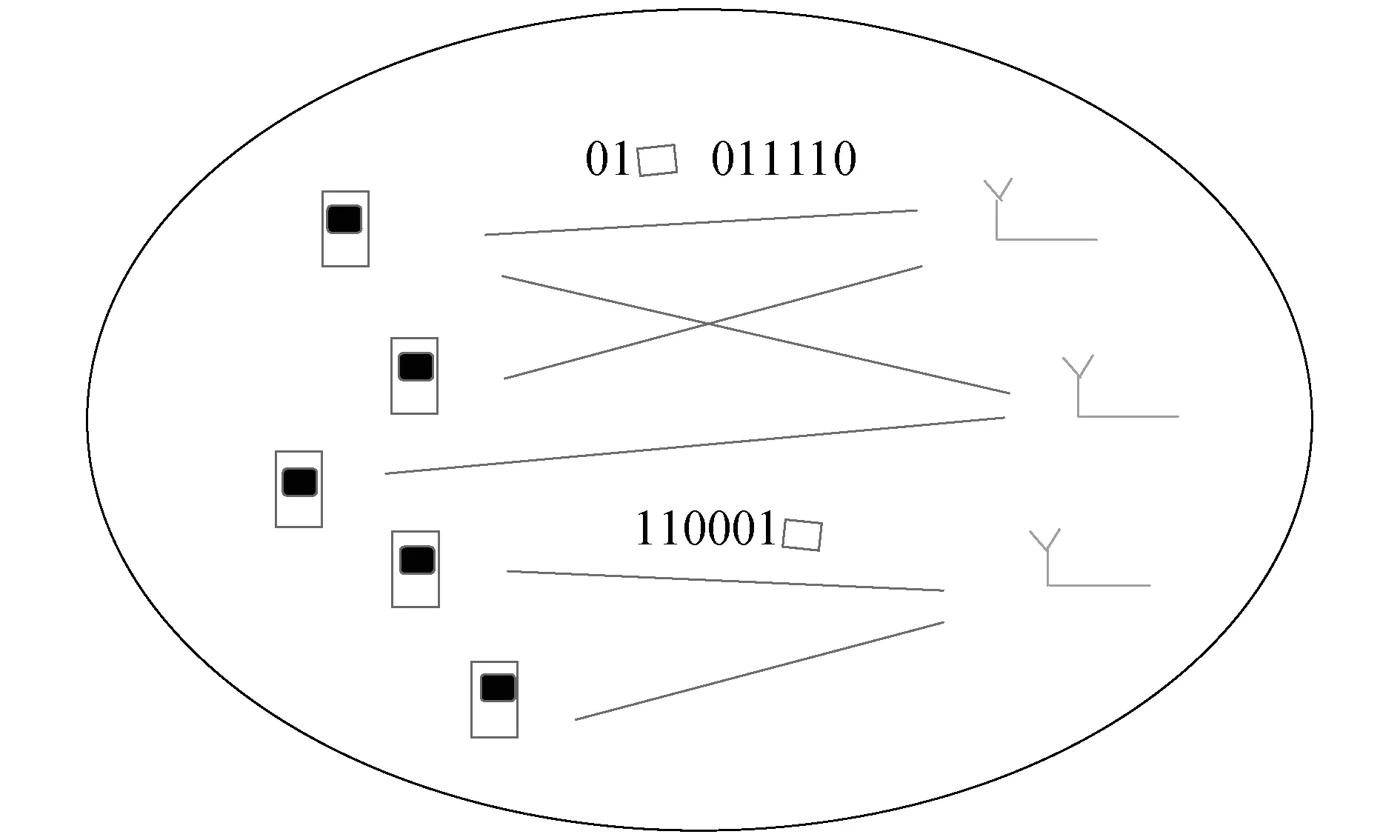
图1 大规模MIMO基本模型

大规模MIMO系统可以表示一个空间复用的多信道模型.信号在空气中传输时,除了自身会发生信息丢失外,各种障碍物也会使得信号发生散射、衍射和反射,导致信息产生误差.大规模MIMO是一个蜂窝小区中拥有M个用户和一个基站,每个用户都有一个天线用于和基站进行信息的收发,基站有N根天线用于信息收发.基本的模型如图1所示.

图1中,左边是用户,右边是基站天线,它们之间形成无线信道,通过收发天线传输二进制码元.

该模型接收信号和用户发送信号的制约关系为:

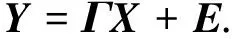
(1)

式中,X是MIMO模型发送端的发送信息数据矩阵,Y是经过无线信道传输后MIMO模型接收到的数据矩阵.Γ是信道参数矩阵,E是干扰矩阵.

2 大规模MIMO低秩张量信息检测

大规模MIMO中,天线之间的收发信道形成了一个二维空间,而这个二维空间的数据在空间上具有相关性.用矩阵来表示所有的传输数据会造成信息的误差,而张量可以更好地表达复杂数据的本质结构,因此采用张量的形式来表示接收信号与发送信号之间的关系更能全面地反应信息的完整性.大规模MIMO的信道是一个二维矩阵,它对应的就是一个二阶张量.

将接收端的码元数据扩展成二维张量后,将每个发送信号的用户看作是一个元素,基站的每个接收天线看作一个元素,这两个元素对应的元素值为该坐标下的码元值,这样信道之间的收发就构成了一个三元元组.每个用户和接收天线之间存在着唯一的对应关系,构建二维张量Y∈RM×N,张量中的每个对应元素为ynm.信息在两个维度的分量矩阵分别是P和Q,通常把这两个分量矩阵称之为因子矩阵,它们对应着张量分别在MIMO模型收发的两个维度上的分量,并且一般是正交的.因子矩阵P为张量在第一维度的分量,Q为张量在第二维度的分量.

默认P的秩为H,Q的秩为R,因此它们的大小分别是P∈RM×H和Q∈RN×R.张量的一般分解模型为:

(2)

式中,p为因子矩阵P的列向量,h是列向量的数目.q是因子矩阵Q的列向量,r是列向量的数目,∘表示向量的外积.

3 大规模MIMO低秩张量信息检测算法

3.1 Tucker分解法

Tucker分解法是将因子矩阵以一个核心矩阵为关联,表示大规模MIMO信道收发的两个维度数据的相关程度,剩余的数据主成分仍然保留在各维度的因子矩阵中.这样的分解方法体现了维度之间矩阵的相关性,同时降低了张量的复杂度.将张量依靠Tucker方法进行分解:

(3)

式中,L为核心矩阵,表示两个维度上的因子矩阵的交互部分,它的大小为H×R.P和Q分别是大小为M×H和N×R的因子矩阵,是张量在两个维度上的主成分.H和R是两个因子矩阵的主成分数目.×(i=p,q)表示矩阵间的乘法,表示张量分解,p和q分别为因子矩阵P和Q的列向量,则(3)式可写为:

(4)

(5)

可以看出经过Tucker分解后的张量维数要远小于没有经过分解的张量维数.Tucker分解的实质是通过分解求得在数据完整的情况下的近似张量,因此最大程度地保留了原来张量的信息,这也是对分解因子矩阵不断优化过程.判定张量是否最优化可以使用优化目标函数

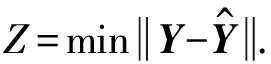
(6)

(7)

其中〈L,L〉=0,将(7)式化简为

(8)

(9)

(9)式表示求出该函数的最大值,就得到优化目标函数的最小值.求解新目标函数的过程就是求解因子矩阵固定值的过程.即用其中一个因子矩阵的解来求出另一个因子矩阵的值.求最优解的过程可以看作一个求解最小秩的过程,因此需要对因子矩阵进行奇异值分解.通过维数的归约,也就是秩的减小,得到核心矩阵L的各维数值,从而确定核心矩阵的维数.将核心矩阵在两个维度上的分量先求解出来,然后将这两个对角矩阵的奇异值从大到小排列,保留一半的值.这样迭代直到核心矩阵归约,得到新的核心矩阵和另一个因子矩阵的之后再代入迭代公式,即可知道其中一个因子矩阵的值.

3.2 改进的Tucker分解法

Tucker分解法将张量分解成一个核心矩阵和两个因子矩阵的形式,其中核心矩阵为两个因子矩阵的交互部分,本文作者提出一种改进的Tucker分解法将Tucker分解法的核心矩阵L变成两个核心矩阵L1和L2,这两个核心矩阵的乘积为原来的核心矩阵,即:

(10)

同样地,在改进的Tucker分解法中有两个维度上的因子矩阵P和Q.大小为H×1,P∈RM×R·Q∈RN×H的大小为R×1,lh和lr分别为P和Q的列向量,L1和L2为两个核心矩阵的元素.改进的Tucker分解为:

(11)

式中,YIT表示改进算法的情况下大规模MIMO接收端的信息,ymn为大规模MIMO接收端二维空间中的对应码元,×i,(i=p,q)表示矩阵间的乘法,表示张量分解.同理存在:

(12)

(13)

与Tucker分解类似,改进的Tucker分解法也是通过求解近似矩阵和保存完整信息的原矩阵之间的差值的平方来得到最优解,将这个最优解设为目标函数:

(14)

从前文可知求解最优解需要固定因子矩阵的具体值也就是先得到每个维度上的分量值,然后在矩阵运算中做收敛运算,当P和Q收敛时停止计算即可得到两者的近似估计值.具体计算过程如下:

1)将没有产生数据误差的张量矩阵进行分解;

2)将该矩阵与误差矩阵进行差值计算,得到优化目标函数fp(Y);

3)通过维度分量矩阵推出因子矩阵P和Q的表达式;

4)当维度矩阵P和Q收敛时停止迭代运算;

5)确定因子矩阵P和Q的值;

6)信息误差得到消除.

4 仿真分析

在大规模MIMO中,信道中传输的信息码元以二进制码(0或1)的交替组合出现.本文作者通过Tucker分解法和改进的Tucker分解法对数据检测性能进行解析,算法的性能指标为信息检测后两种分解法的误码率:

(15)

针对仿真,研究7个仿真数据分别是信噪比为:-10dB,-5dB,0dB,5dB,10dB,15dB,20dB的7个点,对每个点做5次误码率实验,取这5次实验的平均值得到Tucker分解法和改进的Tucker分解法的信噪比与误码率的关系图,如图2所示.

由图2可以看出,改进的Tucker算法误码率总体比Tucker算法小,误码率得到了改善,这是因为改进的Tucker算法中,由于核心矩阵的分解,计算精度更高,数据的检测能力也得到了提高,误码率减小.

图2 信噪比和误码率对应关系图

5 结 论

针对MIMO信道中不可避免的数据误差问题提出了一种基于Tucker算法的改进信息检测方法,该方法将信道中的二进制码元矩阵看作一个张量,从而扩充了信道的信息,用Tucker分解法和改进的Tucker分解法对产生了误差数据的二维张量进行数据检测.但是,张量分解的算法精确度还有待改善,这也是下一步需要研究的问题.

[1] Juho L,Jin-Kyu H.MIMO technologies in 3GPP LTE and LTE-advanced [J].EURASIP Journal on Wireless Communications and Networking,2009(3):1-11.

[2] Vainikainen P,Mustonen M,Kyro M,et al.Recent development of MIMO antennas and their evaluation for small mobile terminals [C].17th International Conference on Microwaves Radar and Wireless Communications,2008,17:1-10.

[3] Dempster A P,Laird N M,Rubin D.Maximan likelihood estimation from incomplete data via the algorithm [J].Journal of the Royal Statistical Society,1977,39(1):1-21.

[4] 金勇进,邵军.缺失数据的统计处理 [M].北京:中国统计出版社,2009.

Jin Y J,Shao J.Statistical processing of missing data [M].Beijing:China Statistics Press,2009.

[5] 龚帅,周小平,李莉,等.基于导频的FBMC/OQAM系统的信道估计方法 [J].上海师范大学学报(自然科学版),2016.45(2):162-165.

Gong S,Zhou X P,Li L,et al.Channel estimation method based on pilot of FBMC/OQAM system [J].Journal of Shanghai Normal University(Natural Sciences),2016,45(2):162-165.

[6] Sehgal M S B,Gondal I,Dooley L S.Collateral missing value imputation:a new robust missing value estimation algorithm for microarray data [J].Bioinfonnatics,2005,21(10):2410-2417.

[7] Zhou X,Wang X,Dougherty E R.Missing-value estimation using linear and non-linear regressionwith Bayesian gene selection [J].Bioinformatics,2003,22(19):2302-2309.

[8] Scholz M,Kaplan R,Guy C L,et al.Non-linear pea;a missing data approach [J].Bioinformatics,2005,21(20):3887-3895.

(责任编辑：包震宇,顾浩然)

The detection algorithm based on low rank tensordecomposition of large-scale MIMO

Liu Xingyue, Zhou Xiaoping, Li Li, Peng Zhangjie

(College of Information,Mechanical and Electrical Engineering,Shanghai Normal University,Shanghai 200234,China)

In this paper,we propose an improved Tucker decomposition algorithm.The tensor is decomposed into two dimensions.By using matrix rank reduction and convergence in both Tucker and improved Tucker algorithm,we get an approximate estimation which can preservewhole information of original tensor completely.The simulation result shows that the improved Tucker decomposition algorithm can enhance the performance of the error detection of the system.

massive MIMO; tensor decomposition; data detection; Tucker algorithm

10.3969/J.ISSN.1000-5137.2017.01.013

2016-11-29

上海市自然基金项目(16ZR1424500)

刘星月(1993-),女,硕士研究生,主要从事大规模MIMO方面的研究.E-mail:291179220@qq.com

导师简介: 周小平(1981-),男,博士,副教授,主要从事宽带无线通信、新一代移动通信和物联网技术方面的研究.E-mail:zxpshnu@163.com(通信联系人)

TN 929.5

A

1000-5137(2017)01-0074-05