基于数值分析的桩-筏复合地基中的筏板应力分析

2017-03-27曾俊铖

福建交通科技 2017年1期

关键词：筏板路堤路基

■曾俊铖

（福建省高速公路有限责任公司，福州350001）

基于数值分析的桩-筏复合地基中的筏板应力分析

■曾俊铖

（福建省高速公路有限责任公司，福州350001）

采用有限差分法分析程序，依据某试验段的工程地质和设计施工情况建立了路堤荷载下桩-筏复合地基数值分析模型，计算分析了桩-筏复合地基中筏板结构上、下表面的三向应力分布规律及不同筏板厚度下的应力变化规律。结果表明筏板上表面横向受压、竖向受压，下表面横向受拉、竖向受压，筏板的设计关键在于控制筏板下表面的横向拉应力；筏板越厚，下表面的横向拉应力分布越均匀，最大拉应力越小。研究成果可为路堤荷载作用下桩-筏复合地基中的筏板设计提供参考。

数值分析复合地基桩-筏应力

桩-筏复合地基是一个由钢筋混凝土板、褥垫层、刚性桩及地基土等几部分组成的（如图1），具有有效地减小地基的不均匀沉降和工后沉降，提高地基的承载力、路基稳定性，缩短施工工期等优势[1]，在路基工程中的深厚软土地基处理中得到应用[2-3]。

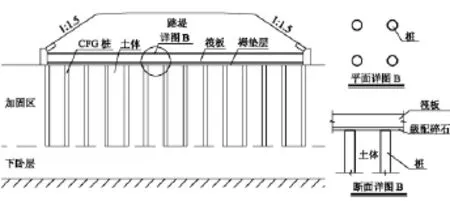
图1 桩-筏复合地基加固示意图

桩-筏复合地基控制沉降的性能优于带帽桩-网复合地基，但造价要比带帽桩-网复合地基高，主要是筏板的造价比桩帽的高。因此，有必要对路堤荷载下桩-筏复合地基中的筏板结构三向应力分布情况进行研究。本文采用有限差分法分析程序，建立了路堤荷载下桩-筏复合地基数值分析模型，计算分析了桩-筏复合地基中筏板结构上、下表面的三向应力分布规律及不同筏板厚度下的应力变化规律，为筏板的优化设计提供参考，以降低筏板造价。

1 桩-筏复合地基数值模型

1.1 模型参数确定

该模型的的工程地质参数和设计施工情况见文献[1]；同时，软硬塑黏土、硬塑黏土、全风化岩、强风化岩的承载力特征值分别为150kPa、200kPa、250kPa、500kPa。数值模型的土层的弹性模量按压缩模量3.5倍取值，全风化岩、强风化岩的弹性模量根据土层承载力特征值由硬塑黏土的模量进行正比例换算，路基的各物理力学参数指标取值见表1。

表1 路基的物理力学指标取值

地基软硬塑黏土厚6.0m、硬塑黏土厚6.0m、全风化岩厚3.0m、强风化岩厚5.0m；刚性桩桩长13.0m，桩间距2.0m，桩直径0.4m，采用正方形布置，混凝土强度等级C20；褥垫层结构为0.2m级配碎石；筏板为钢筋混凝土板，厚度0.5m，混凝土强度等级C25。路基顶面宽13.6m，边坡坡度1∶1.5，路堤填筑高度取4.8m。

1.2 数值模型建立

地基土、桩、筏板、褥垫层及路堤采用实体单元模拟。筏板与填料及褥垫层界面、桩与土界面处分别设置接触单元。筏板和桩体采用弹性本构模型，其余路堤填料及地基土采用Mohr理想弹塑性本构模型。边界条件是模型底部为完全固定约束，模型侧面水平固定约束。因路基横断面沿路基中心线是对称的，数值模型按半断面建立。地基土的计算宽度为半路堤底部宽度的3倍；深度为达到弱风化层顶面，即假定弱风化层不发生沉降；纵断面选取1倍的桩间距作为计算范围。建立路堤荷载下桩-筏复合地基数值模型，如图2所示。

图2 路堤荷载下桩-筏复合地基的路基数值模型

2 筏板上表面应力分布

为了能够直观的表示出应力分布的规律和幅值，本文将筏板的三向应力分布结果绘制成三维图。图中的正值表示拉应力，负值表示压应力；SXX、SYY、SZZ分别代表σx（横向）、σy（纵向）、σz（竖向）。

2.1 σx分布

图3为筏板上表面σx（Pa）分布三维图。从图3可知：桩-筏复合地基在4.8m高的路堤荷载作用下，筏板上表面的σx为压应力，最大压应力位于X=6m和X=8m处，最大压应力约为700kPa；越靠近桩位正上方，筏板上表面的σx越小。这是因为桩对筏板有向上的支承力，支承力会限制筏板局部（桩位正上方）变形，使得桩位正上方的筏板上表面出现受拉状态，而下表面出现受压状态。通过结构力学的叠加原理，路堤荷载的作用和桩的作用叠加，就会出现如图3所示的应力分布情况。

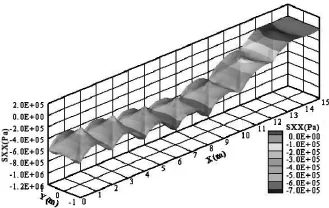
图3 筏板上表面σx（SXX）分布三维图

2.2 σy分布

图4为筏板上表面σy（Pa）分布三维图。从图4可知：筏板上表面的σy有压应力，也有拉应力，应力关于Y轴对称。应力沿Y=0到Y=0.45m（或Y=-0.45m）的发展规律为：从拉应力状态渐变为压应力状态，且拉、压应力的数值大致相当，约为150kPa。

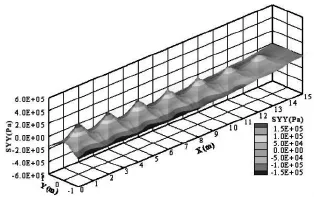
图4 筏板上表面σy（SYY）分布三维图

2.3 σz分布

图5为筏板上表面σz（Pa）分布三维图。从图5可知：筏板上表面σz为压应力，压应力沿Y轴分布比较均匀。上表面σz沿X轴正向逐渐变小，与路堤横截面形状有关。在X=0～7m范围，σz幅值在90～100kPa范围内，与由σz=γH=20×4.8=96kPa相吻合。

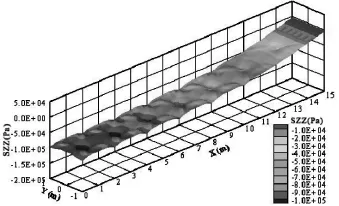
图5 筏板上表面σz（SZZ）分布三维图

3 筏板下表面应力分布

3.1 σx分布

图6为筏板下表面σx（Pa）分布三维图。从图6可知：筏板下表面的σx为拉应力，最大拉应力约为1.0MPa，位于X=6.0m和X=8.0m处，混凝土未开裂。筏板下表面σx关于Y轴对称，沿X轴正方向越来越小，越靠近桩位正上方，σx越小。

3.2 σy分布

图7为筏板下表面σy（Pa）分布三维图。从图7可知：筏板下表面的σy有压应力，也有拉应力，应力关于Y轴对称，分布规律与筏板上表面的关于σy=0对称。应力沿Y=0到Y=0.45m（或Y=-0.45m）的发展规律为：从压应力状态渐变为拉应力状态，且拉、压应力的数值大致相当，约为150kPa。

图6 筏板下表面σx（SXX）分布三维图

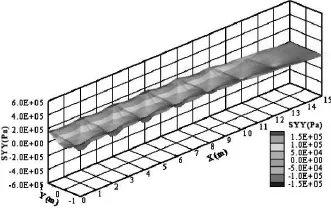
图7 筏板下表面σy（SYY）分布三维图

3.3 σz分布

图8为筏板下表面σz（Pa）分布三维图。从图8可知：筏板下表面σz为压应力，σz在桩顶上方出现明显的应力集中现象。最大压应力约为700kPa。

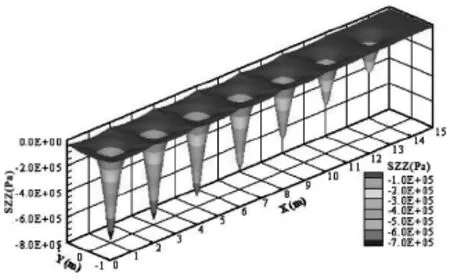
图8 筏板下表面σz（SZZ）分布三维图

4 筏板优化分析

筏板造价的影响因素主要是筏板的厚度和配筋率。一般情况下，路堤荷载作用下筏板的配筋按最小配筋率来设计，即筏板的配筋率取0.2%。在配筋率确定的情况下，筏板厚度成为控制筏板造价的最主要参数。通过筏板厚度的调整，分析不同筏板厚度下表面的σx分布，以优化筏板厚度。筏板厚度分别取0.2m、0.3m、0.4m、0.5m，分析结果如图9所示。

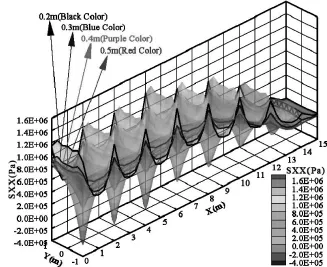
图9 筏板不同厚度（0.2～0.5m）下表面σx（SXX）分布对比三维图

从图中可看出：在两桩中心线位置，筏板厚度越厚，筏板下表面X向最大拉应力越小；在桩顶位置，筏板下表面σx的方向与筏板的厚度有关，筏板厚度较小时σx可能为压应力；筏板越厚，筏板下表面的σx分布越均匀。说明筏板下表面的σx分布与筏板的厚度有关，即与筏板的刚度有关。筏板刚度越大，下表面的σx分布越均匀，X向最大拉应力越小。