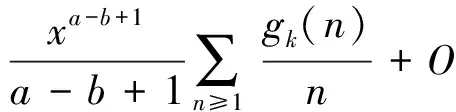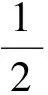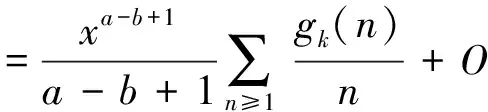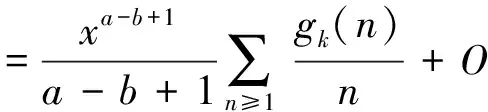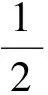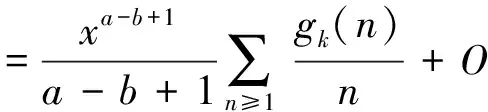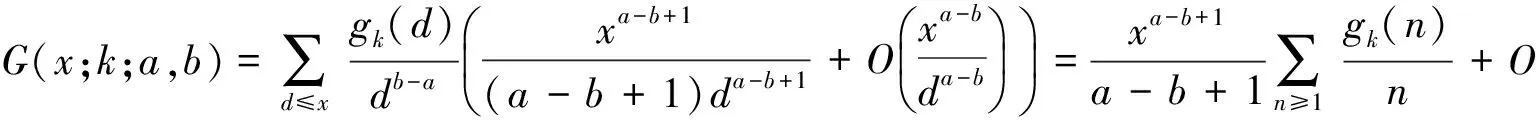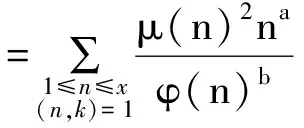无平方因子的正整数的欧拉函数平均值

杨 沛

(华北水利水电大学 数学与信息科学学院，河南 郑州 450045)

无平方因子的正整数的欧拉函数平均值

杨 沛

(华北水利水电大学 数学与信息科学学院，河南 郑州 450045)

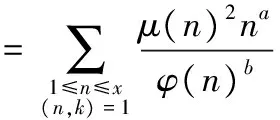
渐近公式；可乘函数；分类讨论

欧拉函数的均值估计对许多数论问题的解决都有重要的推动作用，此估计是数论中一个重要的板块，许多数论问题都需要以此为基础.Goldsron得出了欧拉估计中指数和估计的参数结果，现已知此结果可用来帮助证明华林问题.现在进一步深入研究，重点解决了欧拉函数均值估计中的一个重要和式G(x;k;a,b)的估计值渐近公式，采用莫比乌斯变换与欧拉函数可乘性的性质进行计算，并依据参数分类讨论，最后得出较优的结果，对哥德巴赫猜想和华林问题的参数估计算法都有帮助.

1 主要结果

定理1 对于固定的实数a和b及正整数k，

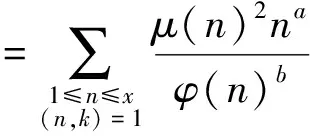
那么

其中

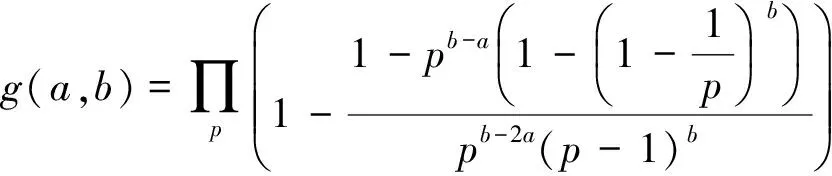
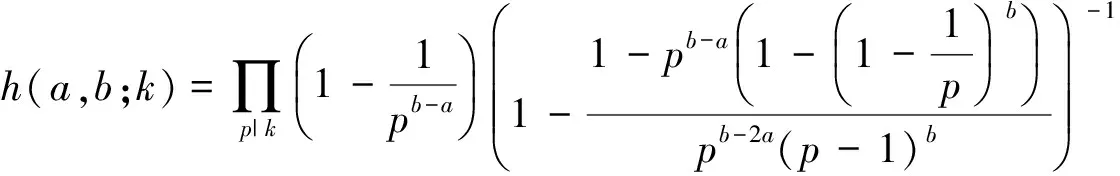
并且

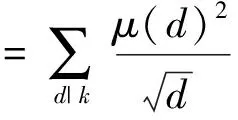
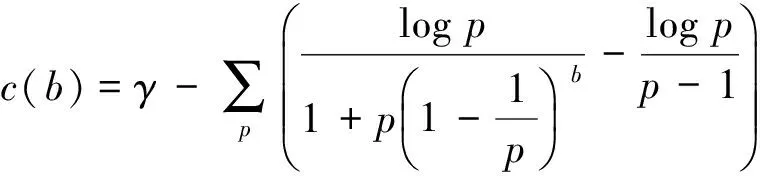
2 引理

先列出证明过程中所需要的引理[1].

引理1 对于固定的实数λ，有如下公式成立:

引理2 对于固定的实数a和b，有如下公式成立:

3 定理1的证明

定义

gk(n)通过如下式定义

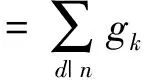
可以计算出如下结论:

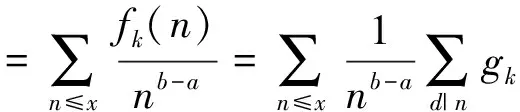
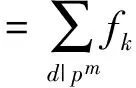
所以可以得到

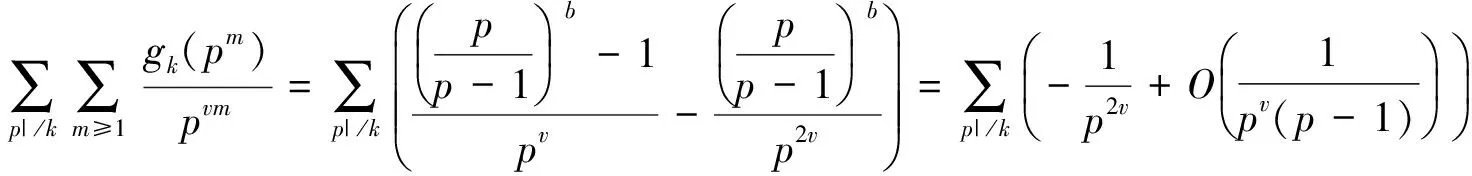
上式收敛，可以得到

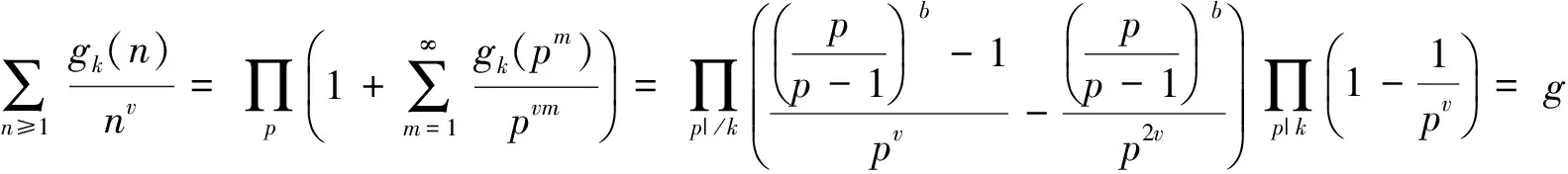
其中

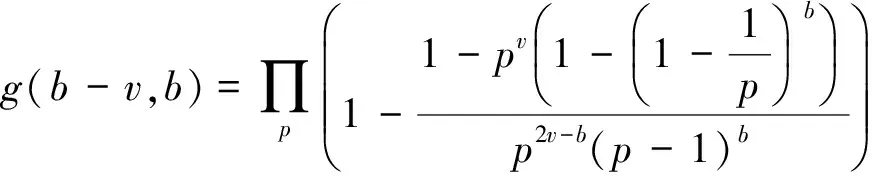
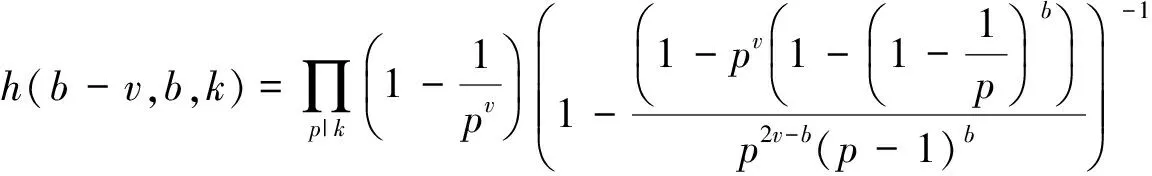
为了保证gk(n)≠0，n需要满足下式[2]

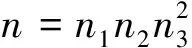
所以

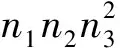
其中

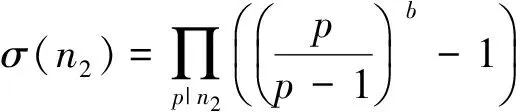
可以得到

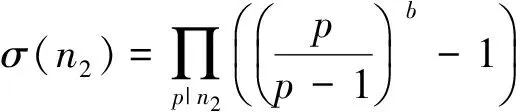
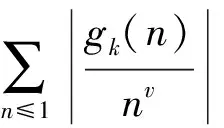
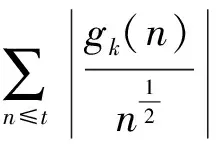
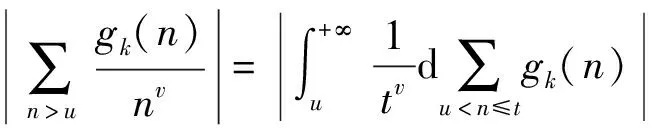
那么

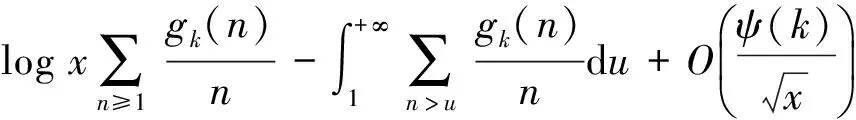
接下来计算下述积分

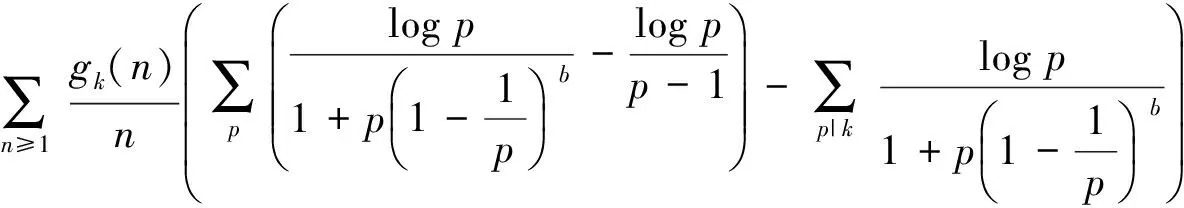
(1)当b-a>1时，由引理2和上述论述可得如下结果:

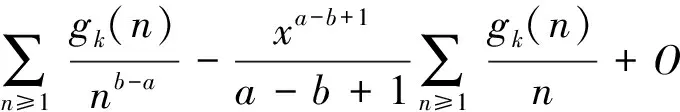
(2)当b-a=1时，可得

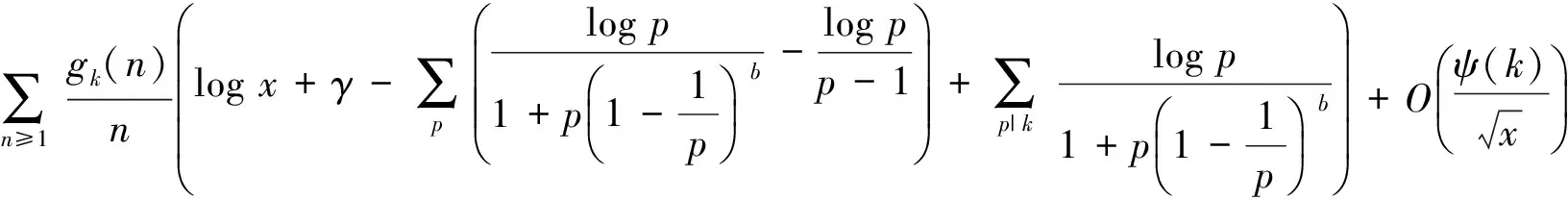
(3)当0

(4)当b-a≤0时，可得

定理1证毕.

[1]GOLDSTONDA.Linnik’stheoremonGoldbachnumbersinshortintervals[J].GlasgowMathematicalJournal,1990,32(3):285-297.

[2]KARATSUBAAA.解析数论基础[M].哈尔滨:哈尔滨工业大学出版社,2012.

[3]MONTGOMERYHL，DAVENPORTH.MultiplicativeNumberTheory[M].Cambridge:CambridgeUniversityPress,2000.

On the mean values of the Euler function of positive integers with square-free

YANG Pei

(MathematicsandInformationScienceSchool,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450045,China)

asymptoticformula;multiplicativefunction;categorizethesituations

2016-12-01

杨沛(1990-)，男，河南郑州人，硕士研究生，主要研究方向为数论.

O

A

1674-330X(2017)01-0076-05