基于GPS、磁罗盘与大气数据计算机的无人机风估计

高艳辉，李志宇，肖前贵

(南京航空航天大学 中小型无人机先进技术工信部重点实验室，南京 210016)

基于GPS、磁罗盘与大气数据计算机的无人机风估计

高艳辉，李志宇，肖前贵

(南京航空航天大学 中小型无人机先进技术工信部重点实验室，南京 210016)

针对无人机实时航路规划及适应环境变化的自主能力发展需求，提出了一种新的风估计与空速校准的方法;该方法基于GPS接收机、大气计算机和磁罗盘等传感器实现;针对定常风模型，风速、风向能够利用地速、风速和空速之间的速度矢量三角形关系计算得到；采用无导扩展卡尔曼滤波(DEKF)，估计风场信息以及真空速的比例校准系数；利用某型无人机数字仿真平台，在2D定常风条件下进行了全过程自主飞行仿真；仿真结果表明：该方法在航路跟随的直线段、转弯段均能准确估计。

风估计；空速校准；无人机；无导扩展卡尔曼滤波

0 引言

无人机(UAV)的机动性与经济性使它在空投、目标跟踪、地理定位等军事、民用领域得到了大量应用。准确的风估计可以大大提高无人机适应环境变化的自主能力。Sohn[1]研究表明风场信息可以提供地面目标的精确定位信息。此外，估计风过程中，同时得到的偏航角有助于提高无人机在航路跟随、着陆任务等方面的控制性能。事实上，风估计本身已经成为气象无人机的一项重要应用[2]。

本文提出了利用GPS接收机、大气数据计算机和磁罗盘输出的测量信息来估计风速、风向的一种新方法。该方法同时也对空速进行了比例校准，便于应用于低成本无人机。该方法不同于以前使用的技术[3-5]，它不需要无人机以特定的机动动作飞行，在航路跟随的直线段、转弯段均能准确估计。

1 风估计算法设计与实现

1.1 风估计算法设计

在风场中无人机飞行运动学满足速度矢量三角形[3]，如图1所示。即：

(1)

图1 速度矢量三角形

无人机导航一般采用地面坐标系，因此，本文选择在地面坐标系进行计算。其中，GPS接收机输出的地速Vg、天向速度Vd和航迹角χg信息为地面坐标系。本文主要考虑2-D定常风模型，包括风速Vw，风向χw两个参数，同样采用地面坐标系。大气数据计算机输出的真空速Va，坐标系为气流坐标系，因此，需要经过机体坐标系、地面坐标系的转换。小型无人机一般采用协调转弯飞行，方向舵主要用于消除侧滑角，因此，假定β≈0。在无人机稳定配平飞行时，迎角一般较小，为计算方便，假定α≈θ。因此，

(2)

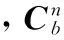
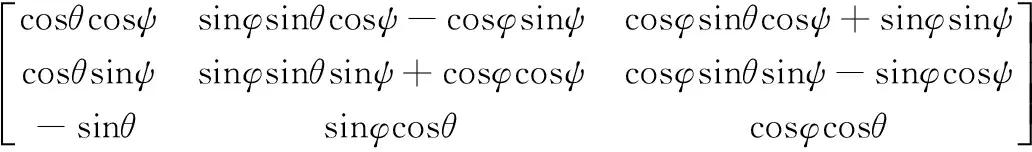
(3)

(4)

一般情况下，无人机平飞迎角非常小，可以假设sinθ≈0。因此，在二维水平面上，得到两个方程：

Vacos2θcosψ=Vgcosχg-Vwcosχw

(5)

Vacos2θsinψ=Vgsinχg-Vwsinχw

(6)

将公式(5)、(6)计算平方和，整理得到：

(7)

大气数据计算机输出的空速V利用空速管测量的总压、静压根据伯努利方程计算得出[4]。

空速管头部和静压孔测得的压力值不完全与真实值相等。假设空速管的迎角较小，那么空速管测量的总压误差就非常小。然而，静压误差却会很大，这是因为静压孔附近的气流由于压力传感器本身和飞机结构的原因受到了干扰。同时对于低成本无人机，空速管每一次的安装位置、方向可能均有不同，导致安装误差变化较大。因此，针对实际大气环境、安装等误差而设置的补偿系数sf。若有迎角、侧滑角存在，无人机真空速与Vpitot之间的关系如下：

(8)

将公式(7)代入公式(8)中，整理得到：

(9)

将公式(6)与公式(5)相除得到：

(10)

ψ=mod(atan2(Vgsinχg-Vwsinχw,Vgcosχg

-Vwcosχ),2π)

(11)

航向角由磁罗盘测量得到。磁罗盘测得的是无人机纵轴以磁北方向为基准的磁方位, 这个磁方位再加上一个修正量(即磁偏角)，才能得到无人机纵轴以正北方向为基准的真方位角。假设无人机飞行区域的磁偏角变化较小, 只要在飞行前根据起飞方向对磁偏角进行校正，就可以忽略磁偏角角对风速测量精度的影响。

1.2DEKF算法

扩展卡尔曼滤波(EKF)基于一阶泰勒级数公式展开式实现，是一种广泛应用于状态估计的技术。EKF算法的一个主要缺点是它的实现。非线性方程所描述的模型需要求导和模型导数(或雅可比矩阵)计算。M.Q.Brendan[11]提出了一种新颖的无导扩展卡尔曼滤波(DEKF)方法。DEKF算法假设状态分布的高阶矩非常小，利用n+1个n维状态向量集来表示状态估计和状态的不确定性。极限情况下，该算法数学上等价于EKF。

本文在此简要描述无导扩展卡尔曼滤波(DEKF)，具体参见文献[11-12]。DEKF同传统卡尔曼滤波器一样分为两个阶段，时间更新阶段与测量更新阶段，为清晰起见，下文省去时间步长索引。

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

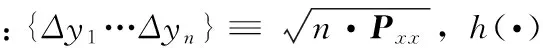
1.3 风估计算法实现

针对2D定常风模型，本文选择DEKF方法同时估计风速、风向和空速校准系数。在某些飞行时间，这些变量基本保持固定不变，因此，可以采用随机游走过程建模[4]。

状态变量x=[Vwχwsf]T，系统动力学描述如下：

x(k+1)=Fx(k)+wk

(21)

其中:F为单位矩阵，w～N(0,Qk)。

在上述公式中，地速、航迹角由GPS接收机测量输出，俯仰角由垂直陀螺测量。这些变量的精度一般较高，在每一个时刻可以当做已知变量处理。测量变量zk=[Vaψ]，非线性观测方程表示为：

(22)

其中:vk～N(0,Rk)，Va参见公式(9),ψ参见公式(11)。

在仿真时，测量噪声、过程噪声根据实际试飞数据统计得到。风速、风向的初值可以根据速度矢量三角形计算得到。

2 仿真验证

2.1 某型无人机仿真平台简介

本文采用某型无人机数字仿真平台进行算法的仿真验证[13]。该平台采用层次化、模块化设计思想构建，总体结构如图2所示。

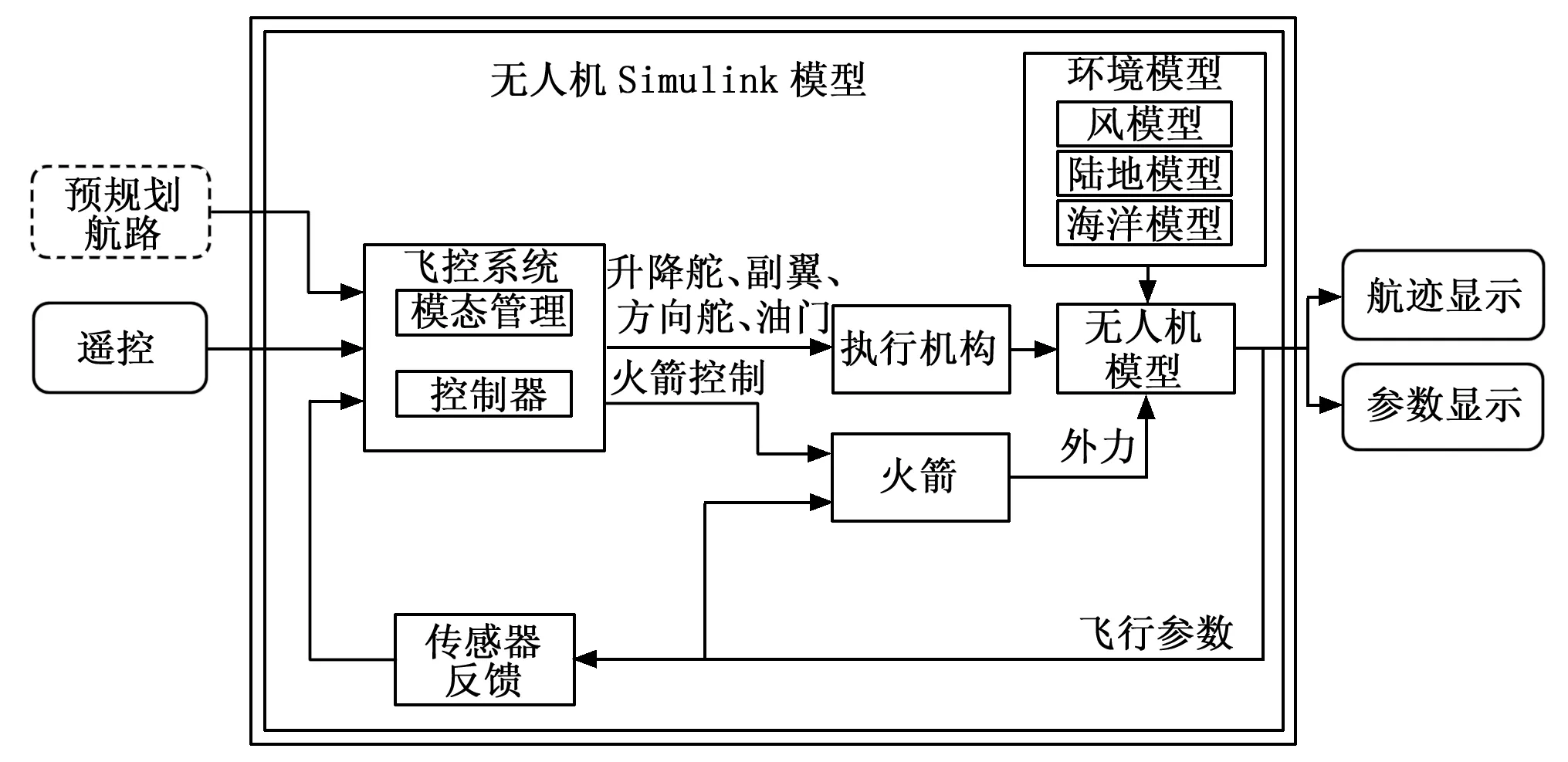
图2 无人机数字仿真平台总体框图

无人机模型接收常规执行机构作为输入，完成无人机空气动力特性、发动机推力特性、质量特性和大气特性等模块的计算，然后求解六自由度非线性全量运动方程，模拟无人机的飞行状态变化。同时也接收来自外部环境模型(例如：定常风)的变化输入。在每一个仿真步长更新的飞行参数，将传递给可视化模块(航迹显示、参数显示)，用于显示、存储仿真数据，便于数据分析。

火箭作用力利用火箭助推器弹道性能预估曲线(推力与时间的关系曲线)模拟计算得到，并通过Stateflow精确控制火箭的作用时间。

传感器反馈模块用于将飞行参数转换为真实的模拟信号输出，这些信号将反馈至飞控系统用于无人机的轨迹控制。传感器模拟模块由AeroSimBlockset提供，根据实际传感器参数进行设置。

飞控系统仿真包含模态管理和控制器两个模块，其中控制器采用embeddedSimulinkFunction的方式来实现。模态管理根据遥控指令以及预规划航路等输入信息，实现无人机的导航与制导、飞行模态的逻辑控制与切换等功能。控制器根据输入的飞行参数、纵向给定量、横航向给定量、纵向飞行模态、横航向飞行模态进行控制律解算，输出升降舵、副翼舵、方向舵和油门信息用来控制无人机实现相应的飞行模态。

执行机构模块用于模拟舵机的转速、频带、零位、迟滞等特性。该模块由AeroSimBlockset提供，根据实际舵机特性进行参数设置。

2.2 仿真过程与结果分析

本文假定校准系数初值为0.9，风速设定为30m/s，风向为32.45°。仿真过程中DKF用到的参数包括：

某型无人机按照航线在无人机数字仿真平台上进行全过程自主飞行仿真。在平飞高度施加定常风干扰，风向与平飞段航线夹角为90°，为正侧风干扰。在无人机飞行稳定后，接通DEKF滤波，风估计、残差以及空速校准的仿真结果如图3、图4所示。

图3 风速、风向、校准系数仿真结果

图4 残差计算结果

图3、图4中，在300s时，仿真平台自动接通DEKF进行风估计。在300～650s，无人机处于直线自主飞行。在接通滤波20s后，风速、风向、校准系数即可快速预测，风速残差小于5m/s,风向残差小于10°，校准系数残差小于0.02。在650～900s，无人机处于180°转弯飞行，风速残差小于0.6m/s,风向残差小于9°,校准系数残差小于0.017。在900～1 100s，无人机处于直线自主飞行状态，在1 100～1 350s无人机处于转弯飞行状态，经过一圈飞行后，风速残差小于0.15m/s,风向残差小于2°,校准系数残差小于0.004 且估计精度进一步提高。在整个飞行过程中，风速、风向、校准系数的估计结果均满足3-sigma边界要求。仿真结果表明：DEKF估计结果可信。

3 结束语

本文提出了一种新的风估计与空速校准的方法。该方法基于GPS接收机、大气计算机、磁罗盘和垂直陀螺等传感器实现。设计的方法利用了地速、风速和空速之间的速度矢量三角形关系，并不依赖于无人机的气动力模型。仿真试验结果表明：推荐的DEKF估计方法，只需要无人机进行半圈自主转弯飞行，就可以获得合理的风速、风向信息。估计的校准系数能够修正真空速到一个合理的水平。因此，本文提出的方法能够减少低成本无人机空速传感器的复杂校准操作，提高真空速的测量精度。同时该方法对于后续无人机在风场中实时航路规划提供了研究基础。

[1] Sohn S, Lee B, Kim J, et al. Vision-based real-time target localization for single-antenna GPS-guided UAV[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44: 1342-1355.

[2] 周伟静, 沈怀荣. 一种基于小型无人机的风场测量方法[J]. 测试技术学报, 2009, 23(4): 297-302.

[3] Hollister WM, Bradford ER, Welch JD. Using Aircraft Radar Tracks to Estimate Winds Aloft[J]. MIT Lincoln Laboratory Journal, 1989, 2:555-565.

[4] Cho A, Kim J, Lee S, et al. Wind Estimation and Airspeed Calibration Using a UAV with a Single-Antenna GPS Receiver and Pitot Tube[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1):109-115.

[5] Pachter M, Ceccarell N, Chandler PR. Estimating MAV's Heading and the Wind Speed and Direction Using GPS, Inertial, and Air Speed Measurements[A]. Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit[C]. Honolulu, Hawaii, 2008.

[6] Langelaan JW, Alley N, Neidhoefer J. Wind Field Estimation for Small Unmanned Aerial Vehicles[J]. Journal of Guidance, Control, and Dynamics, 2010, 34(4):1016-1030.

[7] Ceccarelli N, Enright JJ, Frazzoli E, et al. Micro UAV Path Planning for Reconnaissance in Wind[A]. American Control Conference[C]. New York, NY, USA, 2007:5310-5315.

[8] Osborne J, Rysdyk R. Waypoint Guidance for Small UAVs in Wind[C]. AIAA Infotech@Aerospace, 2005.

[9] Palanthandalam-Madapusi HJ, Girard A, Bernstein DS. Wind-field Reconstruction Using Flight Data using an unbiased minimum-variance unscented filter[J]. Transactions of the Institute of Measurement and Control, 2008, 33(6):718-733.

[10] Phillips WF. Mechanics of Flight[M]. Canada: John Wiley & Sons, Inc. 2004.

[11] Brendan M Q. A derivative-free implementation of the extended Kalman filter[J]. Automatica, 2006, 42(11): 1927-1934.

[12] Xuedong Wu, Zhihuan Song. Online Chaotic Time-series Prediction with the Derivative-Free Extended Kalman Filter[C]. Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, Chian, 2008.

[13] 高艳辉, 肖前贵, 徐义华, 等. 无人机数字仿真平台的设计与实现[J]. 指挥控制与仿真, 2014, 36(1): 104-110.

[14] 沈怀荣, 邵琼玲, 王盛军, 等. 无人机气象探测技术[M]. 北京: 清华大学出版社, 2010.

Wind Estimation for UAV Based on GPS, Magnetic Compass and Air Data Computer

Gao Yanhui, Li Zhiyu, Xiao Qiangui

(Key Laboratory of Unmanned Aerial Vehicle Technology ( Nanjing University of Aeronautics and Astronautics), Ministry of Industry and Information Technology, Nanjing 210016, China)

Aiming at the requirements of real-time path planning and autonomous capability for adapting to the environmental changes of Unmanned Aerial Vehicle (UAV), a new method for wind estimation and airspeed calibration is proposed. Based on the information of GPS receiver, air data computer and magnetic compass, the method is implemented. Aiming at constant wind mode, the wind speed and wind direction can be estimated using velocity triangle vector between ground speed, wind speed and airspeed. A Derivative-free extended Kalman filter (DEKF) is applied to estimate wind parameters and scaling factor of airspeed. Using a digital simulation platform for Unmanned Aerial Vehicle (UAV), an entire autonomic flight simulation were achieved in 2D wind field. Simulations results show that wind speed and wind direction can be accurately estimated both in straight line and turning segment during the path tracking by using the method.

wind estimation; airspeed calibration; UAV; DEKF

2016-12-31；

2016-02-14。

中国人民解放军装备部预研基金项目(51325010601)。

高艳辉(1976-)，男，河北辛集人，硕士，助理研究员，主要从事无人机飞控系统方向的研究。

1671-4598(2017)03-0231-03DOI：10.16526/j.cnki.11-4762/tp

N945.13;V

A