四旋翼无人机可视化轨迹跟踪仿真系统

许江阴，赵宏强,2，邓 宇,2

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083； 2.山河智能装备股份有限公司，长沙 410100)

四旋翼无人机可视化轨迹跟踪仿真系统

许江阴1，赵宏强1,2，邓 宇1,2

(1.中南大学 高性能复杂制造国家重点实验室，长沙 410083； 2.山河智能装备股份有限公司，长沙 410100)

为了便于对四旋翼无人机控制算法进行实验仿真和验证，联合Solidworks和Matlab/SimMechanics工具箱设计了一种四旋翼无人机可视化轨迹跟踪仿真系统；利用Solidworks搭建了四旋翼无人机三维实体模型，并通过Solidworks和Matlab转换接口将该实体模型导入到Matlab/SimMechanics中；Matlab/SimMechanics提供了了三维可视化窗口，可以显示无人机的实时仿真状态；仿真平台在Matlab/SimMechanics环境中实现，与Matlab/Simulink通信方便，可方便的将Simulink设计好的控制算法添加到仿真系统中，以进行验证和参数整定，还具有姿态分析和数据分析等功能；轨迹跟踪仿真结果表明，四旋翼无人机可视化轨迹跟踪仿真系统直观可视，准确可靠，能较好地对控制算法进行研究和测试，对四旋翼无人机以及控制算法的研究和开发具有重要价值。

四旋翼无人机；可视化仿真系统；实体建模；轨迹跟踪

0 引言

随着新型材料、微惯导、微机电及飞行控制等技术不断发展，多旋翼无人机以其结构简单、机动性强、飞行方式独特引起了广泛关注，成为国际上研究的热点之一[1]。本文所研究的四旋翼无人机是多旋翼无人机中的一种，具有体积小，重量轻，结构紧凑对称等优点。四旋翼无人机是一个具有六个空间自由度和4个输入的非线性欠驱动多输入多输出系统，其控制算法的设计一直是国内外的研究热点[2-3]。许多控制算法都在四旋翼无人机上有所应用，如PID控制[4-5]、滑模控制[6]、神经网络控制[7]、反步法[8-9]、模糊控制[10-11]等。对控制算法的仿真验证是四旋翼无人机试飞前最重要的一部分，目前很多研究都采用数值数据进行仿真，无法直观的表示无人机的实时位置和姿态，因此，设计一种可以在四旋翼无人机试飞前进行可视化仿真，降低开发成本，提高控制算法开发效率[12-13]的三维可视化仿真系统引起了研究者的广泛兴趣。殷强等人[12]结合FlightGear模拟飞行软件和Mtalab/Simulink建立四旋翼无人机可视化系统。周德新等人[13]通过C++语言设计了一个用于验证飞行控制系统的全数字仿真平台，可视化显示窗口采用了民航飞机中的FPD(Primary Flight Display，主飞行显示器)界面进行显示。

本文开发了一种基于Solidworks和Matlab/SimMechanics的四旋翼无人机可视化轨迹跟踪仿真系统，首先，通过物理建模的方式对四旋翼无人机进行可视化建模，然后在Simulink里搭建轨迹跟踪控制模块,对四旋翼无人机PID控制算法进行可视化轨迹跟踪仿真分析。该仿真系统可以在四旋翼无人机进行试飞之前，模拟实际飞行状态，即在可视化实验环境条件下对飞控算法的可靠性进行验证和参数调整，对四旋翼无人机的实际飞行状态进行评估，提高调试效率，减少实际试飞中由于控制算法错误带来的不必要损失，保证实际飞行试验的安全。

1 四旋翼无人机的运动学分析

四旋翼无人机通过控制4个电机的转速来改变螺旋桨的速度，从而控制四旋翼无人机的飞行姿态和位置。四旋翼无人机有十字型和X型两种结构，本文研究的是X型结构的四旋翼无人机，机头方向为1号和3号电机夹角平分线的正前方，其中 1号和2号电机逆时针转动，3号和4号电机顺时针转动，规定顺时针方向为正，如图1所示。对四旋翼无人机进行运动学分析，首先对四旋翼无人机做出如下假设：

(1)四旋翼无人机为完全对称的刚体，忽略其结构和弹性变形；

(2)机体坐标系与四旋翼无人机的质心重合；

(3)假设地面坐标系为惯性坐标系。

图1 X型四旋翼无人机结构图

在机体坐标系里，单个电机驱动旋翼所产生的升力为Fi=kbwi2，力矩为Ti=kdwi2，其中i=(1,2,3,4)，kb表示升力系数，kd为转矩系数，wi为第i个电机的角速度。定义欧拉角η=[φθψ]T，φ为滚转角，θ为俯仰角，ψ为偏航角,无人机角速度Ω=[p,q,r]，忽略空气阻力，体坐标系下四旋翼无人机受到的推力Fb：

(1)

Fb通过转换矩阵R转换到惯性坐标系下无人机受力Fg:

Fg=RFb-mgEz

(2)

R为从体坐标系到惯性坐标系的转换矩阵：

R=

(3)

在惯性坐标系下，由牛顿第二定律F=ma，结合(1)、(2)、(3)式可得线性位移方程：

(4)

(5)

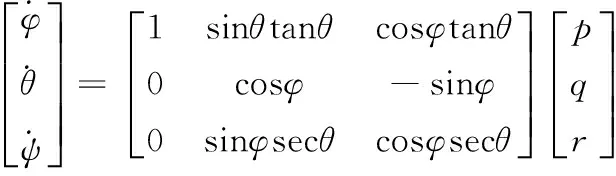
(6)

当姿态角变化较小时认为式(6)可以简化为:

(7)

由(5)和(7)式可得:

(8)

取:

(9)

其中:l为电机中心到机体坐标系的距离:

则:

Mx=u2,My=u3,Mz=u4

(10)

由式(4)、(8)、(9)、(10)可得四旋翼无人机的运动学方程:

(11)

2 Solidworks和Matlab可视化联合仿真系统设计

2.1 搭建四旋翼无人机可视化仿真模型

Solidworks是Windows环境下的三维实体设计软件，Solidworks工作界面简洁直观，可以随时修改特征，来改变零部件的形状和尺寸，并且在装配的环境里，可以方便地设计和修改零部件，具有强大的实体建模功能。同时，Matlab下的SimMechanics功能工具箱里提供了大量模块，使用这些模块可以方便的建立机构运动的模型，不仅可以进行机械系统的单独分析，还可以与Simulink设计的控制器及其它动态系统相连进行综合仿真以及控制策略的研究[14-16],但SimMechanics在三维建模方面功能有限，因此，本文根据现有的四旋翼无人机的形状和尺寸，先用Solidworks对四旋翼无人机进行三维实体建模，然后再导入到Matlab下的SimMechanics中，并与设计的控制器进行连接。因为四旋翼无人机是通过4个电机来控制无人机的运动，所以为了使生成的SimMechanics模型更加简洁，将四旋翼无人机分为机体和4个电机-螺旋桨五部分，这就需要将四旋翼无人机在Solidworks中按照这五部分进行装配。

Solidworks导入到Matlab的步骤：

建立Solidworks和Matlab接口，在Solidworks安装SimMechanicsLink插件，然后用Solidworks打开建立的四旋翼无人机模型.SLDASM，如图2，输出为二代SimMechanics的.xml文件。

图2 四旋翼无人机Solidworks模型

打开Matlab，输入smimport(‘.xml文件名’)，将生成四旋翼无人机的SimMechanics模型，如图3，其可视化模型如图4，从图中可以看出整个机构由地坐标系、机体和4个电机-螺旋桨模块组成，其中机体与电机-螺旋桨通过单自由度模块连接。

SimMechanics模型可以与Simulink的控制系统模型方便的结合，SimMechanics提供了驱动模块和传感器模块与Simulink的其他模块进行信号传递，在同一个环境中对控制器和受控对象建模，进行仿真分析。由于四旋翼无人机具有6个空间自由度，所以在地坐标系与机体、4个电机-螺旋桨之间添加六自由度模块，并在六自由度模块上添加位置和角度传感器，修改模块里的重力方向使之与仿真图中的z轴方向一致，对模型中的4个单自由度模块添加所需的驱动力矩模块以及由力矩产生的转速传感器模块，并将其传递给对应的螺旋桨，带动螺旋桨转动，此时Matlab里的四旋翼的无人机SimMechanics模型已搭建好，如图5。

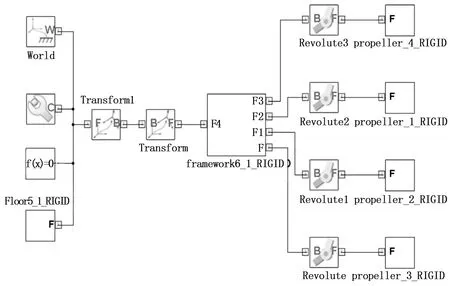
图3 四旋翼无人机SimMechanics模型

图4 四旋翼无人机SimMechanics可视化模型

2.2 设计PID控制模块

因为PID控制具有结构简单、调整方便、控制可靠、稳定性好等优点，在工业控制上具有广泛的应用，所以本文采用PID控制算法控制四旋翼无人机的轨迹跟踪。PID控制由比例、积分、微分3个单元组成，PID控制规律就是对偏差e(t)进行比例、积分、微分变换的控制规律，表示为：

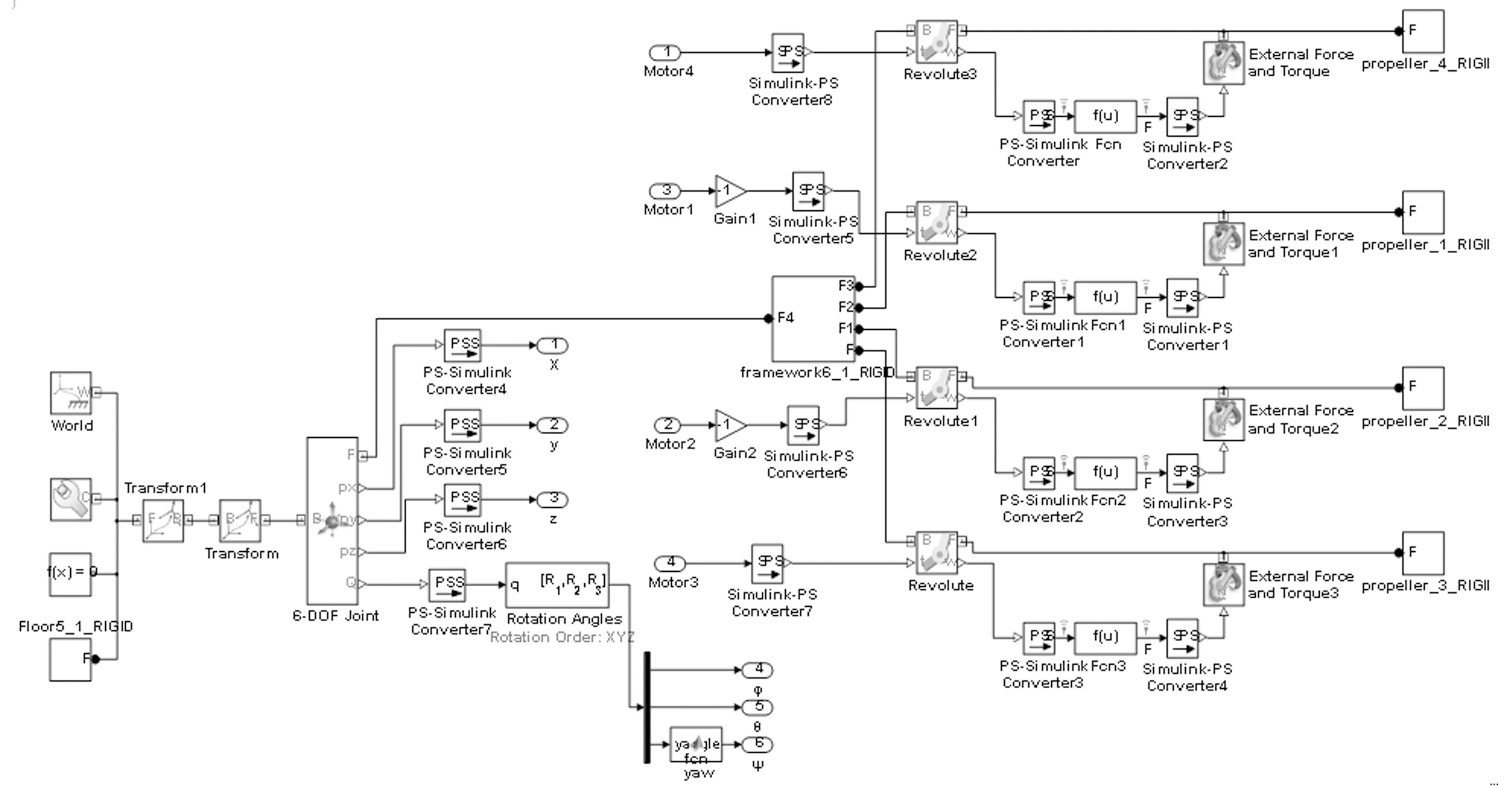
图5 已添加驱动的四旋翼无人机SimMechanics模型

(12)

其中为比例控制项，为比例系数；为积分控制项，为积分时间常数；为微分控制项，为微分时间常数。

本文采用内外环PID控制算法控制四旋翼无人机的飞行姿态，内环采用PID控制无人机的姿态角，外环采用PD控制无人机的位置。系统输入量为目标的期望位置x1,y1,z1，期望偏航角ψ1，由位置控制器计算出期望的滚转角φ1，俯仰角θ1，根据期望的姿态角和高度由姿态控制器和运动学逆解计算出四旋翼无人机4个电机所需要的转矩控制量，输入到四旋翼无人机模型中，接下来在Matlab的Simulink模块里搭建四旋翼无人机的轨迹跟踪控制模块并在可视化仿真系统里对其进行验证，四旋翼无人机轨迹跟踪系统的Simulink仿真模型，如图6。

图6 四旋翼无人机轨迹跟踪控制Simulink框图

3 四旋翼无人机轨迹跟踪系统仿真分析

为验证四旋翼无人机可视化轨迹跟踪系统的可靠性，对所设计的PID轨迹跟踪控制算法进行仿真，四旋翼无人机的初始位置为：x=0,y=0,z=0,期望的输入轨迹为：x1=cos(t),y1=sin(t),z1=1,ψ1=0，输出为四旋翼无人机的实际轨迹为x,y,z,ψ,仿真结果如图7～11，图7为四旋翼无人机的可视化运动仿真图，其中图(a)为四旋翼无人机的侧视图，图(b)为四旋翼无人机在2s时的俯视图，图(c)为四旋翼无人机在4s时的俯视图，图(d)为四旋翼无人机在6s时的俯视图。

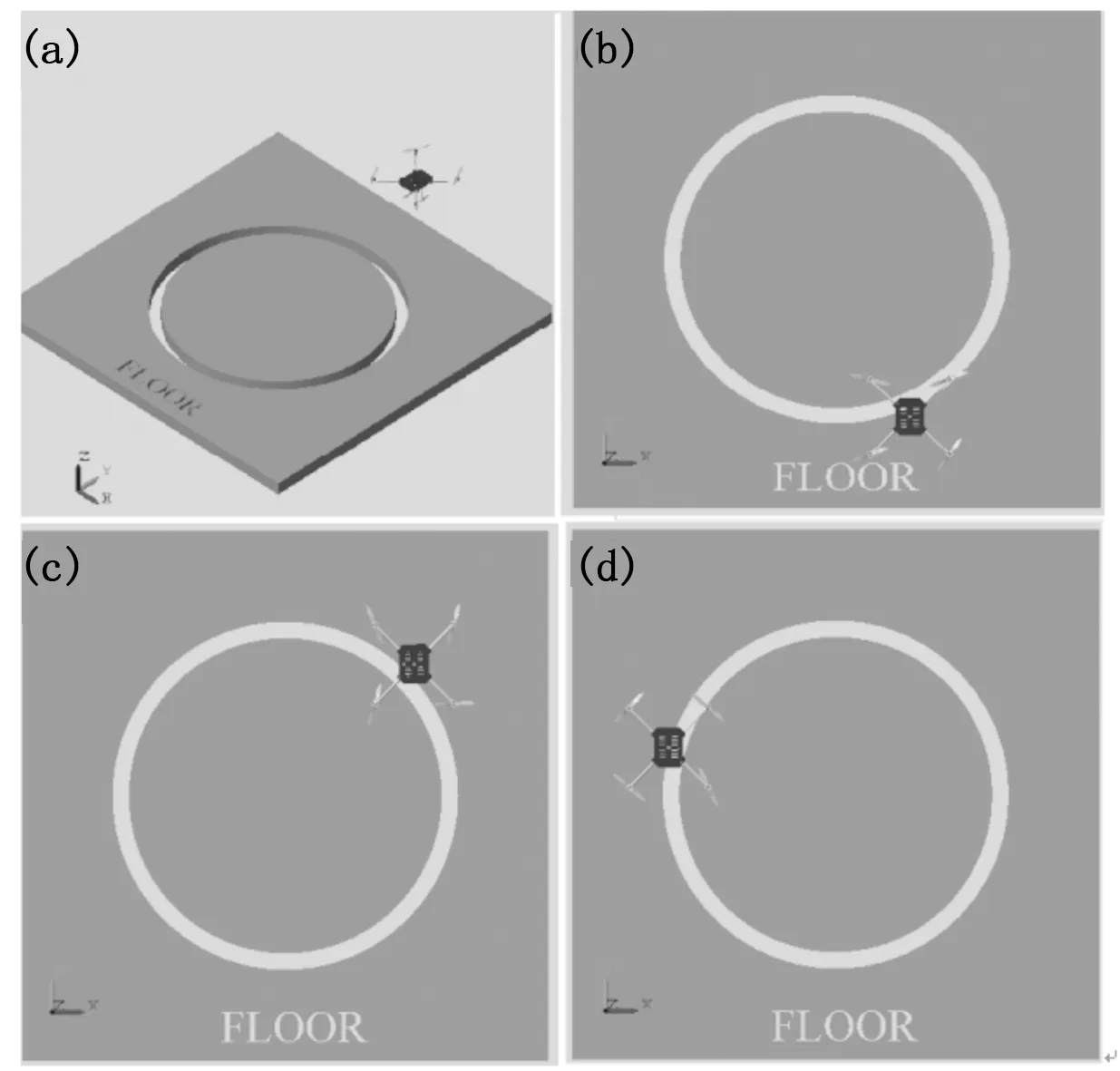
图7 四旋翼无人机可视化运动仿真图

图8为X轴方向的轨迹跟踪曲线，由图可知在t=0时刻，在X轴上的目标坐标与实际坐标相差1 m，经过2s后基本能的跟踪X轴上的轨迹变化，图9为Y轴方向的轨迹跟踪曲线，由图可知在起飞稳定后也能基本的跟踪上Y轴的轨迹变化，图10为高度方向的跟踪曲线，由图可知在1 s左右高度有一个超调量，3 s左右恢复到目标位置，跟踪误差基本为零。图11为偏航角跟踪曲线，由图可知刚开始偏航角有波动，在3 s左右恢复正常。整个仿真过程在仿真系统里直观可视，效果逼真，数据处理清晰明确。

图8 X轴方向的轨迹跟踪曲线

图9 Y轴方向的轨迹跟踪曲线

图10 高度方向的跟踪曲线

4 结论

本文基于Solidworks强大的三维建模功能以及Solidworks和Matlab/SimMechanics的转换接口，快速建立四旋翼无人机的SimMechanics可视化模型，结合Simulink里设计的轨迹跟踪控制器，搭建四旋翼无人机可视化轨迹跟踪仿真系统。四旋翼无人机可视化轨迹跟踪仿真系统具备实体机控制算法仿真及分析功能，可以直观地显示四旋翼无人机的实时飞行状态，使用方便，结果逼真。四旋翼无人机可视化轨迹跟踪仿真系统能

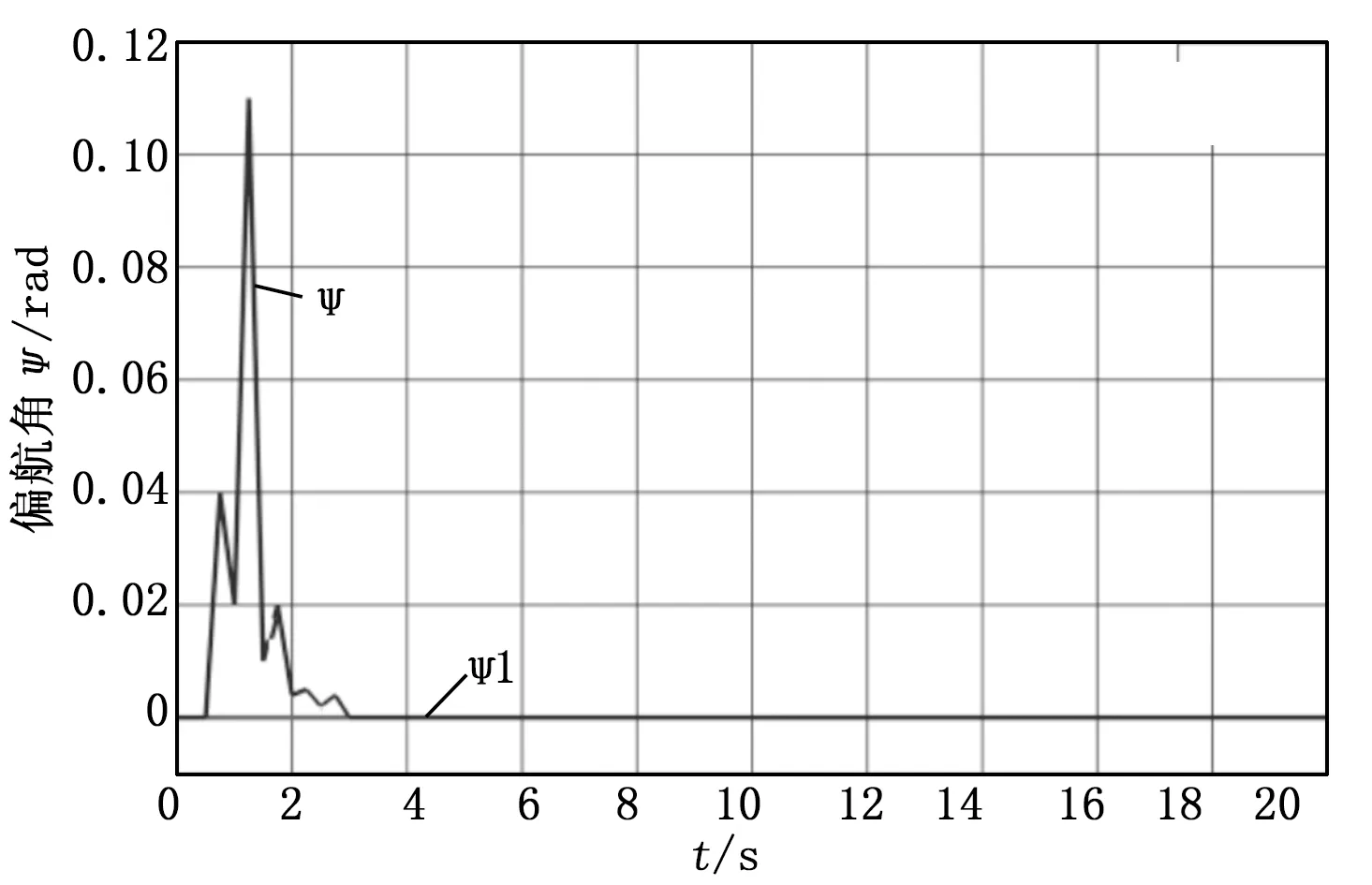
图11 偏航角跟踪曲线

较好的对控制算法进行可视化动态仿真与验证，提高四旋翼无人机控制算法的研究效率，降低开发成本。

[1] 苏哲宇.一种微小型四旋翼飞行器控制系统的设计与开发[D].沈阳：东北大学,2012.

[2] 杨明志,王 敏.四旋翼微型飞行器控制系统设计[J].计算机测量与控制, 2008, 16(4):485-487.

[3] 王 璐.四旋翼无人飞行器控制技术研究[D].哈尔滨：哈尔滨工程大学,2012.

[4]SalihAL,MoghavvemiM,MohamedHAF,etal.ModellingandPIDcontrollerdesignforaquadrotorunmannedairvehicle[A].IEEEInternationalConferenceonAutomationQualityandTestingRobotics[C].IEEE, 2010:1-5.

[5] 周红坤.微型旋翼无人机航迹规划与航迹跟踪控制系统设计[D].成都：电子科技大学, 2015.

[6] 贾燕波,杨 峰,秦绪菲.基于滑模控制的四旋翼飞行器控制算法研究[J].山东师范大学学报(自然科学版),2014(4).

[7] 黄晓雷,钱正祥,赵 博,等.神经网络直接逆控制在无人机飞控系统中的应用研究[J]. 计算机测量与控制, 2008, 16(10):1448-1450.

[8]HuangM,XianB,DiaoC,etal.Adaptivetrackingcontrolofunderactuatedquadrotorunmannedaerialvehiclesviabackstepping[C].IEEE, 2010:2076-2081.

[9]SteinbergM.NonlinearAdaptiveFlightControlwithaBacksteppingDesignApproach[J]. 1998.

[10] 段凤阳,陈 鹏,郝 爽.无人机姿态控制器设计及仿真[J].计算机测量与控制, 2015, 23(5):1571-1574.

[11] 杨恩泉,高金源.无人机机动轨迹跟踪系统设计[J]. 飞行力学, 2007, 25(2):30-33.

[12] 殷 强,鲜 斌,张 垚,等.四旋翼无人机可视化仿真系统研究[A].中国自动化学会控制理论专业委员会C卷[C]. 2011.

[13] 周德新,马腾达.四旋翼无人机飞控系统仿真平台研究[J]. 计算机测量与控制, 2014, 22(2):424-426.

[14] 杨树川,邵金龙,杨术明,等.基于Solidworks&SimMechanics的机构运动分析与仿真[J]. 河北工业科技, 2011, 28(4):221-225.

[15] 陈爱波,宁淑荣,陈五一.基于MATLAB与SolidWorks的六自由度机器人联合建模仿真[J].机电技术,2014(6):57-60.

[16] 姚太克.一类三自由度并联机构的特性研究与优化设计[D].合肥：中国科学技术大学, 2013.

Visual Trajectory Tracking Simulation System for Quadrotor UAV

Xu Jiangyin1,Zhao Hongqiang1,2, Deng Yu1,2

(1.Central South University, Changsha 410083, China;2.Sunward Intelligent Equipment CO., Ltd., Changsha 410100, China)

In order to facilitate the simulation and verification of the quadrotor UAV control algorithm，combination of Solidworks and Matlab/SimMechanics toolbox designed a quadrotor UAV visual trajectory tracking simulation system. Using Solidworks built a quadrotor UAV three-dimensional entity model and imported the model into Matlab/SimMechanics through Solidworks and Matlab conversion interface. Matlab / SimMechanics provides a three-dimensional visualization window, and can display the status of real-time simulation of UAV. Simulation platform is realized in Matlab/SimMechanics environment, and easy to communicate with Matlab/Simulink, and can added control algorithm designed by Simulink to simulation system easily for verification and parameter tuning, also has posture analysis and data analysis and other functions. The result of trajectory tracking simulation show that quadrotor UAV visual trajectory tracking simulation system is intuitive and visual, accurate and reliable, and can research and test of control algorithm. It has important value for the research and development of the quadrotor UAV and control algorithm.

quadrotor UAV; visual simulation system；entity modeling; trajectory tracking

2016-06-30；

2016-11-02。

国家科技支撑计划(2014BAD06B07-1); 湖南省军民融合专项。

许江阴(1990-)，女，河南商丘人，硕士研究生，主要从事控制理论与工程方向的研究。

1671-4598(2017)03-0130-04

10.16526/j.cnki.11-4762/tp.2017.03.036

TP391.9

A