采用分段行-列核2DPCA的高光谱图像降维

向英杰，杨 桄，张俭峰，王 琪



采用分段行-列核2DPCA的高光谱图像降维

向英杰，杨 桄，张俭峰，王 琪

（空军航空大学，吉林 长春 130000）

二维主成分方法计算时间少，降维效果好，被成功应用到高光谱图像降维中。基于二维主成分方法，为挖掘高光谱图像的非线性信息，实现了分段行-列核2DPCA方法的降维，并对比分析了行-列2DPCA方法、分段行-列2DPCA方法和行-列核2DPCA方法的降维效果。利用相关性将高光谱图像划分为5个子空间，通过转换数据结构来实现行和列的核2DPCA变换，最后将行和列结果进行融合得到降维结果。降维结果表明，在较高信息保持率情况下，分段行-列核2DPCA方法具有最高的图像清晰度和边缘强度。不同地物像元像素折线图表明，分段行-列核2DPCA方法能更好地区分不同地物，可以很好地应用于地物分类和目标识别。

核二维主成分分析；分段行-列2DPCA；高光谱图像；数据模型转换；降维

0 引言

高光谱遥感可以在可见光到红外电磁波谱范围内，以较窄的波段间隔对目标区域内的地物连续成像，从而使获取的数据具有“图像立方体”的形式和结构，并且具有“图谱合一”的特性和优势[1-2]。正因为如此，使得高光谱数据呈现波段多、数据量大、冗余度强的特点。

如何保留用于分析的重要信息并且有效去除大量的数据维数是尤为重要的工作。作为一种经典的线性降维方法，主成分分析（Principal Component Analysis, PCA）已经广泛应用于高光谱遥感影像的降维。但是PCA方法需要将图像矩阵展开为向量，忽略了各波段图像矩阵的结构信息，并且带来巨大的计算量。基于PCA的不足，Yang等[3]提出了二维主成分分析（Two Dimensional Principal Analysis, 2DPCA），并成功应用于人脸检测。随后，研究人员考虑图像行和列方向的信息，提出了双向二维主成分分析[4]和双边二维主成分分析[5]，取得了较好的识别效果。针对非线性信息的提取，基于核函数的2DPCA方法（K2DPCA）被提出[6-7]，并用于人脸识别，提高了识别率。

在高光谱影像降维领域，研究人员运用2DPCA方法进行降维，提出了多种算法[8-10]。针对高光谱影像中非线性结构，白杨等提出了一种改进的核2DPCA高光谱遥感图像降维方法[11]，能够较好地保持非线性信息。但是高光谱图像各波段之间的相关性大小不一样，按照整体进行二维主成分分析时，一些局部的重要波段由于在前几个主成分中的作用不是特别明显，可能会在波段选择中被忽略，导致结果不准确。同时，单一的某一方向上的2DPCA变换难以去除高光谱图像波段间的相关性。

为了更好去除高光谱影像的相关性并且提取非线性信息，提出了一种分段行-列二维核主成分的高光谱影像降维方法。首先将一组多维的高光谱影像根据波段间的相关性划分成多组波段子集数据，然后在每组波段图像上进行核2DPCA变换，提取列方向的主成分，接着对旋转后的高光谱数据模型进行核2DPCA变换，提取行方向的主成分，最后对得到的主成分进行图像重建。

1 分段行-列核2DPCA的图像降维

1.1 二维主成分分析

设一幅高光谱图像有个波段，每个波段的图像大小为×，则一幅××的高光谱数据可表示为＝{1,2,…,,…,}，其中表示图像的第波段。2DPCA高光谱图像降维步骤如下：

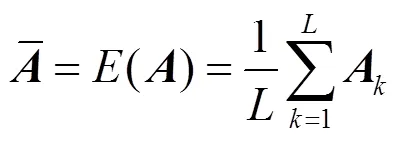
2）计算的协方差矩阵：

式中：t为×的非负定矩阵。

3）计算t的特征值，选取前个最大的特征值1≥2≥…≥及其与之对应的特征向量1,2,…,，令＝[1,2,…,]，称为最优投影矩阵。

4）分别将每个波段图像投影到上：

＝，＝1,2,…,，＝1,2,…,(3)

5）图像重构

由于1,2,…,正交，重构图像为：

式中：的大小通常通过主成分的累计贡献率来确定。

1.2 核二维主成分分析

核2DPCA首先将高光谱影像非线性映射到一个高维空间，然后在核空间中对样本影像进行2DPCA变换。高光谱图像矩阵为，设＝[1,2,…,]，＝1,2, …,其中表示影像第波段的第行。因此，核2DPCA变换具体步骤如下：

1）将影像通过非线性变换:®()投影到高维空间。

()＝[(1),(2), …,()]T(5)

2）计算其样本图像的协方差矩阵t

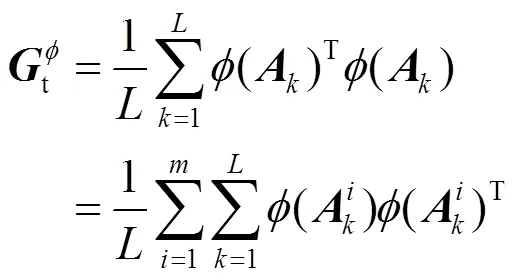
3）计算特征值和特征向量。计算t的特征值和特征向量。存在系数(＝1,2,…,；＝1,2,…,)满足：

可得：

＝ (8)

式中：核矩阵＝()T()，其特征向量为＝[11,，…,]，则前个最大特征向量为1,,…,。由(6)式归一化特征向量，则核2DPCA的投影矩阵为＝[1,2,…,]。

4）计算图像到上的投影。高光谱遥感图像各波段经核2DPCA变换后的主成分为：

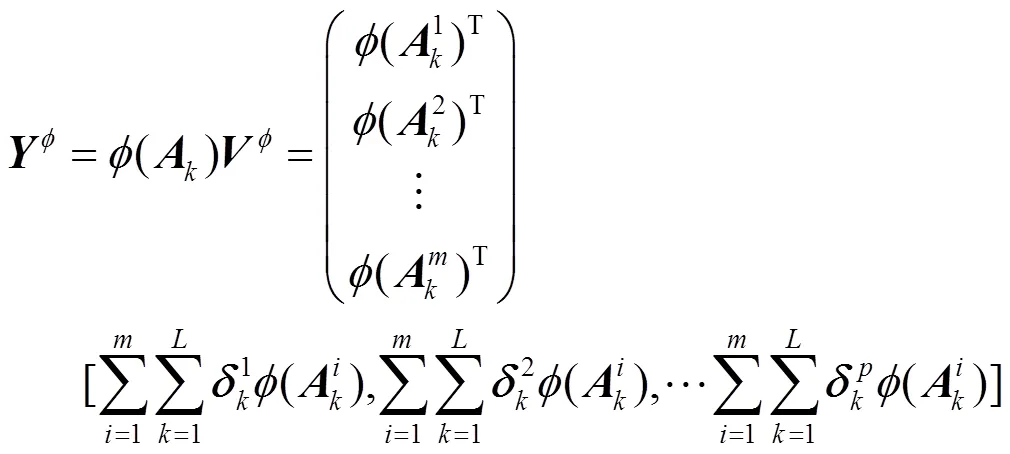
2 本文算法描述

2.1 波段子空间划分

高光谱影像各波段之间的相关性大小不一样，且各波段反映的光谱特性不同。对高光谱影像整体进行核2DPCA变换时，一些局部的重要波段由于在前几个主成分中的作用不是特别明显，可能会在波段选择中被忽略，导致结果不准确，同时考虑到运算时间因素。因此需要将高光谱影像按照相关性进行波段子空间的划分，然后进行核二维主成分分析，本文采用相关系数对高光谱影像进行分段[12]。

首先计算各波段之间的相关系数矩阵，然后采用搜索的方法将相关性超过某一阈值的波段合成一系列波段组。具体过程为：设阈值为，计算第一波段与后面波段的相关系数，若相关系数大于阈值则该波段为第一组波段；若相关系数小于阈值，则将该波段作为第二组的第一波段，计算此波段与后面波段的相关系数并合并分组，直到检测完所有波段。

2.2 高光谱数据模型转换

对高光谱影像进行2DPCA变换实质上是基于单方向的2DPCA变换，它消除了行（列）的相关性，进行了影像列（行）方向的集中，但同时也保留了列（行）方向的相关性。为了消除行列双向的相关性，需要对影像进行行-列2DPCA变换。为了减少计算量，需要将高光谱数据进行转换。

高光谱源图像数据结构通常按照BSQ结构储存，也就是按照波段顺序储存，如图1(a)所示。从前往后依次为第一波段、第二波段、…、第波段，每个波段是大小为×的图像矩阵，从而形成图1(a)所示的“立方体”。将此源图像进行核2DPCA变换，每个波段图像被压缩成×的矩阵，明显不是降维的结果，还需要复杂的矩阵运算进行图像重构。为此，需要将高光谱源图像数据结构进行转换。

图1(a)表示高光谱源图像数据结构，将此源图像沿着轴向左旋转90°，得到如图1(b)所示的结构。此时，高光谱影像变成大小为××的三维数据，仍将其看成BSQ储存形式，从前往后看，每个波段大小为×，共个波段。将每个波段进行核2DPCA变换，得到个大小为×1的向量，从而实现了原始高光谱影像列方向的压缩。然后将图1(b)所示的数据结构以底边为轴向前旋转90°，得到大小为××的三维数据，如图1(c)所示。仍将其看成BSQ储存形式，从前往后看，每个波段大小为×，共个波段。将每个波段进行核2DPCA变换，得到个大小为×1的向量，从而实现了原始高光谱影像行方向的集中。

2.3 行-列主成分融合

将图1(b)中的数据结构进行核2DPCA变换，实现了影像列方向的集中，消除了行的相关性，但忽视了列的相关性。将图1(c)中的数据结构进行核2DPCA变换，实现了影像列方向的压缩，消除的是列的相关性，遗留了行的相关性。但在实际应用中，行和列两个方向的信息是同等重要的，需要将行-列两个方向的主成分进行融合得到最终的降维结果。为了便于实验，本文采用平均加权的融合方法。

2.4 算法实验步骤

本文首先对高光谱影像进行波段子空间划分，然后通过变换高光谱数据结构进行行-列两个方向的核2DPCA变换，得到行-列两个方向的主成分图像，最后运用加权的方式将行-列主成分图像进行融合，得到最终的降维结果。具体步骤如下：

1）波段子空间划分。通过设定相关系数阈值，对高光谱影像进行波段子空间划分，实现影像的分段。

2）列核2DPCA变换。将图1(b)的高光谱数据进行核2DPCA变换，得到第一、第二、……、第主成分，每个主成分是大小为×1的向量，称为列主成分。

3）行核2DPCA变换。将图1(c)的高光谱数据进行核2DPCA变换，得到第一、第二、……、第主成分，每个主成分是大小为×1的向量，称为行主成分。

图1 高光谱图像数据结构转换

Fig.1 Structure transformation of hyperspectral image

4）图像重构。将步骤2）所获取的个列第一主成分依次排列形成列方向的核2DPCA变换的第一主成分图像，个列第二主成分排列成列方向的第二主成分图像，同样可以获取列方向的第三、第四、……、第主成分图像；同理将步骤3）所获取的个行方向的主成分向量对应依次排列，得到行方向的各个主成分图像。

5）行-列主成分图像融合。采用平均加权的方法分别将行-列第1主成分两幅图像、第2主成分两幅图像、……、第主成分两幅图像进行融合，得到最终的第1主成分，第2主成分直到第主成分图像。

3 实验结果和分析

3.1 实验数据

实验中采用两个高光谱影像，数据一是美国AVIRIS传感器获取的圣迭哥机场数据。该图像有220个波段，地面分辨率为3.5m。去掉去除水汽、噪声污染严重的波段，用于实验的总共有189个波段。为了便于验证非线性信息提取效果，截取大小为200×200且包含边缘纹理信息较多的区域，如图2所示。

图2 圣迭哥机场数据

3.2 分段与降维结果

首先根据计算相关系数矩阵对实验影像进行波段子空间划分，实验数据相邻波段的相关系数曲线如图3所示。可以看出，波段间的相关系数大小不同，可以根据相关系数对波段进行子空间划分。为了更好地消除相关性，设定相关系数阈值为0.9，将波段划分为1～30、31～37、38～96、97～135和136～189共5个子空间。

根据本文的算法步骤，对实验数据进行分段行-列核2DPCA变换，得到降维结果。考虑到运算时间和效果[6]，本文选取(,)＝(×)为核函数，阶数取2。同时为了对比降维效果，实验还实现了行-列2DPCA、分段行-列2DPCA以及行-列核2DPCA方法降维。根据前面的子空间划分，行-列2DPCA方法和行-列核2DPCA方法选取前5个主成分，分段行-列2DPCA和本文方法取每个子空间的第1主成分。实验结果如图4所示。

图3 相邻波段相关系数曲线

从图4中可以看出，行-列2DPCA方法所得结果的第一主成分图像清晰，包含了大部分信息，其后四个主成分包含信息量依次递减；分段行-列2DPCA方法所得结果分别为5个波段子空间的第一主成分，图像各个主成分清晰度较不分段方法有很大的提升；行-列核2DPCA方法所得结果各个主成分图像包含信息量依次递减，与行-列2DPCA方法相比该方法各个分量更能表现图像的纹理信息；分段行-列核2DPCA方法所得结果各个主成分图像最清晰，纹理信息更加明显。

为了更加客观定量地比较4种算法的性能，现用信息保持率、图像清晰度、边缘强度和计算时间4个指标来对比分析，如表1所示。考虑到不分段方法主成分递减的问题，在计算上述指标时，不分段方法计算前两个主成分的指标并求平均值，分段方法计算全部5个主成分的指标并求平均值。可以看出，4种方法的信息保持率均达到90%以上，且不分段两种方法高于分段两种方法，同时行-列核2DPCA高于行-列2DPCA，分段行-列核2DPCA高于分段行-列2DPCA。本文方法的图像清晰度和边缘强度相比于其他3种方法都有较大的提升。由于核方法的特性，行-列核2DPCA和分段行-列核2DPCA两种方法的计算时间相对较长，行-列2DPCA的时间最短为10.94s。

图4 四种方法前5个主成分

Fig.4 The first five components of four methods

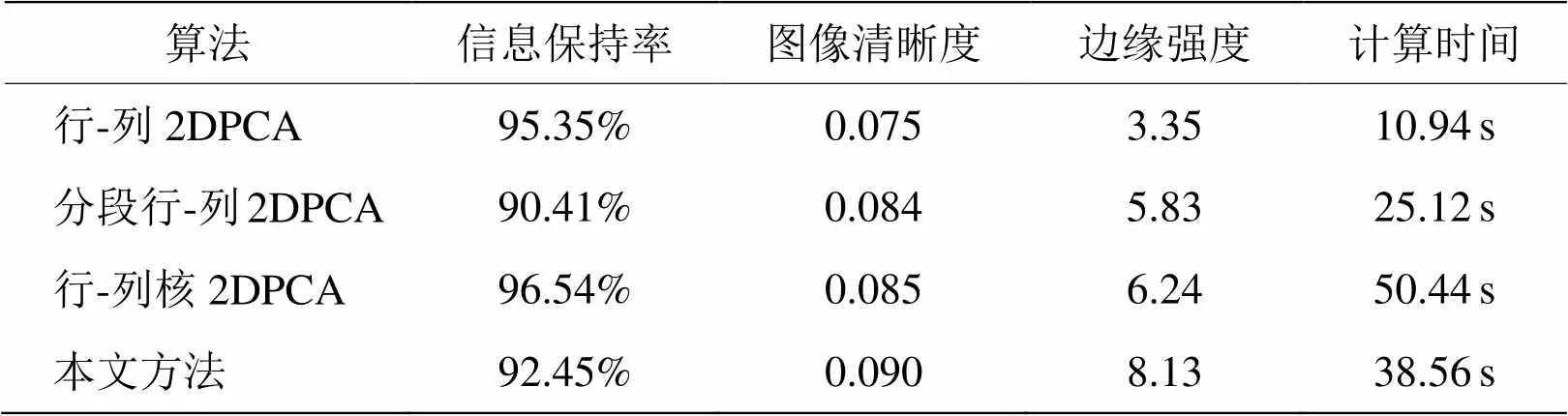
表1 四种算法的客观指标

3.3 像元像素折线图

高光谱图像降维是高光谱图像处理的必要环节，降维后的图像才能更好地应用于地物分类和目标识别。因此，为了更好的评价本文方法，选取原始图像中的A、B、C、D、E五个不同位置的像元，它们分别为飞机、停机坪、道路、草地和房屋，如图5所示。为进行比较，图6绘制了4种方法得到的降维图像中这5个点的像元像素折线图。

由地物可分性特性可知，降维结果各主成分中不同地物像元像素值差别越大，像元折线图曲线上下分得“越开”，地物可分性越好。从图6可以看出，行-列2DPCA和行-列核2DPCA方法得到的降维结果前3个主成分不同地物的像素值差别较大，因此能够较好地区分不同的地物，后两个主成分不同地物像素值几乎没有差别，则不能分辨不同地物，并且行-列核2DPCA方法区分地物效果要比行-列2DPCA方法更好；分段行-列2DPCA和分段行-列核2DPCA方法得到的降维结果的全部前5个主成分不同地物像素值差别均较大，因此均能够较好地区分不同地物，且分段行-列核2DPCA方法区分地物效果比分段行-列2DPCA方法更好；总之，分段行-列核2DPCA方法得到的结果中不同地物区分度最好，从而能够更好地用于后续的地物分类和目标识别等应用。

图5 不同目标像元图

4 结论

2DPCA降维方法省去了复杂的矩阵变换，大大减少了运算时间，同时针对2DPCA降维方法不能提取高光谱图像非线性信息的问题，本文实现了分段行-列核2DPCA的高光谱图像降维，并分析讨论了分段行-列和不分段行-列核2DPCA降维结果的性能。首先采用相关系数的方法将原始高光谱图像分为5个波段子空间，对每个子空间进行行-列核2DPCA变换得到5个主成分。其中，进行行-列核2DPCA变换时将高光谱数据结构进行转换，有效减少了计算量。实验表明，在信息保持率很高的情况下，本文方法降维结果具有最高的图像清晰度和边缘强度。同时绘制了5个不同地物的像元折线图，结果表明本文方法比其他3种方法更能区分不同地物，能够很好地用于地物分类和目标识别。

图6 不同地物像元像素折线图

[1] 张兵. 高光谱图像处理与信息提取前沿[J]. 遥感学报, 2016, 20(5): 1061-1090.

ZHANG Bing. The advances of hyperspectral image processing and information extraction[J]., 2016, 20(5): 1061-1090.

[2] José M, Antonio Plaza, Gustavo Camps, et al. Hyperspectral remote sensing data analysis and future challenges[J]., 2013, 1(2): 6-36.

[3] YANG J, ZHANG D. Two-dimensional PCA: a new approach to appearance -based face representation and recognition[J]., 2004, 26(1): 131 -137.

[4] ZHANG D Q, ZHOU Z H. (2D)2PCA:Two-directional two-dimensional PCA for efficient face representation and recognition[J]., 2005, 69(1-3): 224-231.

[5] YANG J, XU Y, YANG J Y. Bi-2DPCA: A fast face coding method for recognition[J]., 2010(2): 313-340.

[6] Wahyuningrum R T, Damayanti E. Efficient kernel-based two -dimensional principal component analysis for smile stages recognition[J]., 2012, 10(1): 113-118.

[7] SUN N, WANG H X, JI Z H, et al. An efficient algorithm for Kernel two-dimensional principal component analysis[J]., 2008, 17: 59-64.

[8] 赵春晖, 宋晓玥. 基于二维主成分分析的高光谱遥感图像降维[J]. 黑龙江大学自然科学学报, 2009, 26(5): 684-688.

ZHAO C H, SONG X Y. Hyperspectral remote sensing image dimension reduction based on two-dimensional principal component analysis[J]., 2009, 26(5): 684-688.

[9] 张婧, 孙俊喜, 阮光诗, 等. 分段2维主成分分析的超光谱图像波段选择[J]. 中国图形图象学报, 2014, 19(2): 328-332.

ZHANG J, SUN J X, RUAN G S, et al. Segmented 2DPCA algorithm for band selection of hyperspectral image[J]., 2014, 19(2): 328-332.

[10] 杨明, 张鹏强, 余旭初, 等.采用二维主成分分析的高光谱影像分类[J]. 测绘科学, 2015, 40(6): 139-145.

YANG M, ZHANG P Q, YU X C, et al. Hyperspectral image classification using two- dimensional principal component analysis[J]., 2015, 40(6): 139-145.

[11] 白杨, 赵银娣, 韩天庆. 一种改进的K2DPCA高光谱遥感图像降维方法[J]. 测绘科学, 2014, 39(7): 126-139.

BAI Y, ZHAO Y T, HAN T Q. An improved K2DPCA dimension reduction method for hyperspectral remote sensing images[J]., 2014, 39(7): 126-139.

[12] 赵春晖, 胡春梅, 石红. 采用选择性分段PCA算法的高光谱图像异常检测[J]. 哈尔滨工程大学学报, 2011, 32(1): 109-113.

ZHAO C H, HU C M, SHI H. Anomaly detection for a hyperspectral image by using a selective section principal component analysis algorithm[J]., 2011, 32(1): 109-113.

Dimensionality Reduction for Hyperspectral Image Using a Segmented Row-column Kernel Two-dimensional Principal Component Analysis Method

XIANG Yingjie，YANG Guang，ZHANG Jianfeng，WANG Qi

(,130000,)

Two-dimensional principal component analysis (2DPCA) is successfully applied to a hyperspectral image, and is less time-consuming with better dimensionality reduction performance. Based on the two-dimensional principal component method, the segmented row-column kernel 2DPCA algorithm is realized to excavate non-linear information. The dimension reduction effect of the row-column 2DPCA method, the segmented row-column 2DPCA method, and the row-column kernel 2DPCA method are compared and analyzed. The hyperspectral image is divided into five subspaces by correlation, and the kernel 2DPCA of rows and columns is realized by transforming the data structure. Finally, the row and column results are merged to obtain dimensionality reduction results. The reduced dimension results show that the segmented row-column kernel 2DPCA method has the highest figure definition and edge intensity at a higher information retention rate. The pixel line graph indicates that the proposed method can distinguish the different features better, and is well suited to classification and target recognition.

kernel 2DPCA，segmentation row-column 2DPCA，hyperspectral image，data structure transformation，dimensionality reduction

TP751.1

A

1001-8891(2017)12-1107-07

2017-02-23；

2017-04-05.

向英杰（1993-），男，硕士研究生，主要研究方向为高光谱图像解译。E-mail：xyjandsy@163.com。

杨桄（1975-），男，博士，教授，主要从事遥感图像解译等方面研究。E-mail：yg2599@126.com。

吉林省教育厅“十二五”科研项目（2015448）；吉林省科技发展计划资助项目（20140101213JC）。