混凝土弹性模量对混凝土防渗墙应力影响的数值分析
2017-03-25
(辽宁省东水西调工程建设局沈阳市110003)
混凝土弹性模量对混凝土防渗墙应力影响的数值分析
罗东翔
(辽宁省东水西调工程建设局沈阳市110003)
近年来混凝土防渗墙作为一种重要方案用于土石坝的防渗处理,而低弹模混凝土由于对不均匀应力应变的适应能力更强,得到广泛应用。鉴于低弹模混凝土在类似除险加固工程中的重要性,拟对不同弹性模量对防渗墙的影响作计算和分析,得出该工程实例弹性模量的合理取值,以期对类似除险加固工程有一定借鉴作用。
Midas/GTS低弹模混凝土防渗墙数值模拟
1960年以来,对普通混凝土掺入一定黏土或膨胀土等材料的塑性混凝土(弹性模量小于1 000 MPa)在国际上出现,并开始应用于土石坝坝体防渗处理。1980年以来,介于塑性混凝土和普通混凝土之间的低弹模混凝土开始应用于我国江苏和浙江省内众多的大坝防渗加固,但弹性模量一般在17 000 MPa左右。而在2000年之后,多数水库的防渗处理均采用了更低的弹模数值,例如浙江省对河口水库除险加固采用混凝土弹模数值≤2 500 MPa、浙江省长潭水库除险加固采用混凝土弹模数值≤1 250 MPa、浙江省通济桥水库除险加固采用混凝土弹模数值≤3 000 MPa等。国内部分水库的低弹模混凝土弹性模量和抗压(拉)强度指标见表1。

表1 国内部分水库低弹模防渗墙的弹模与抗压(拉)强度指标
本工程实例同为水库除险加固工程,坝体为粘土心墙坝,坝高38.5 m,防渗墙将施工于原坝体粘土心墙内,且最大深度达41.80 m,如采用常规混凝土,墙体弹性模量较高,在水荷载的作用下将出现较大的变形及应力集中现象,产生的拉应力有可能使墙体发生裂缝,进而影响防渗效果,故采用低弹模混凝土。介于此,拟对特定条件下,不同弹性模量对防渗墙的影响作计算和分析,得出该工程实例弹模的合理取值,以期对类似除险加固工程给予一定借鉴。
1 计算基本资料
水库特征水位:死水位为93.00 m;正常蓄水位为122.50 m;校核洪水位(P=0.05%)为125.12 m;设计洪水位(P=2%)为124.33 m。计算所需的参数参照国内外类似工程及类似材料的非线性应力~应变参数,并结合地质钻探资料选取大坝、坝基材料参数值(表2),坝体结果如图1。
表2中材料编号为:1—坝基砂卵砾石;2—坝体心墙粘土;3—坝体砂砾石;4—浸水后坝基砂卵砾石;5—浸水后坝体心墙粘土;6—浸水后坝体砂砾石;7—混凝土防渗墙(E=1 000、1 500、2 000、3 000、5 000、8 000 MPa)。

表2 坝体材料参数表

图1 坝体结构断面图
2 SDAP程序计算
采用中国水利水电科学研究院提供的SDAP程序,计算模型采用E-υ模型,采用逐次增量的方法模拟材料的非线性特性。
计算时选取坝体最大断面。计算工况选取正常蓄水位与校核洪水位情况。计算中考虑防渗墙底部与基岩之间设一层0.1 m厚的沉碴。防渗墙墙体材料采用低弹模混凝土,混凝土弹性模量分别取1 000 MPa、1500MPa、2000MPa、2500MPa、3000MPa、5000 MPa、8 000 MPa。防渗墙应力计算结果见表3。
弹性模量取2 500 MPa时,防渗墙最大拉应力分别为0.56 MPa和0.92 MPa,当弹性模量取5 000 MPa时,防渗墙最大拉应力分别1.37 MPa和2.01 MPa,最大拉应力均位于83.70 m高程左右。不同弹性模量对应最大压(拉)应力关系曲线见图2。

表3 坝体应力应变计算成果表MPa

图2 弹性模量与最大压(拉)应力关系曲线
3 Midas/GTS软件对比计算
利用Midas/GTS强大的几何建模技术建立三维实体模型,模型采用整体建模,实体模型如图3和图4,离散后共有实体单元28 410个,定义材料属性。计算中将上游面水头作为定水头边界处理,下游水位为零,坝基按透水边界处理,坝下游面为透水边界。
图3 不包含基岩的坝体三维实体模型
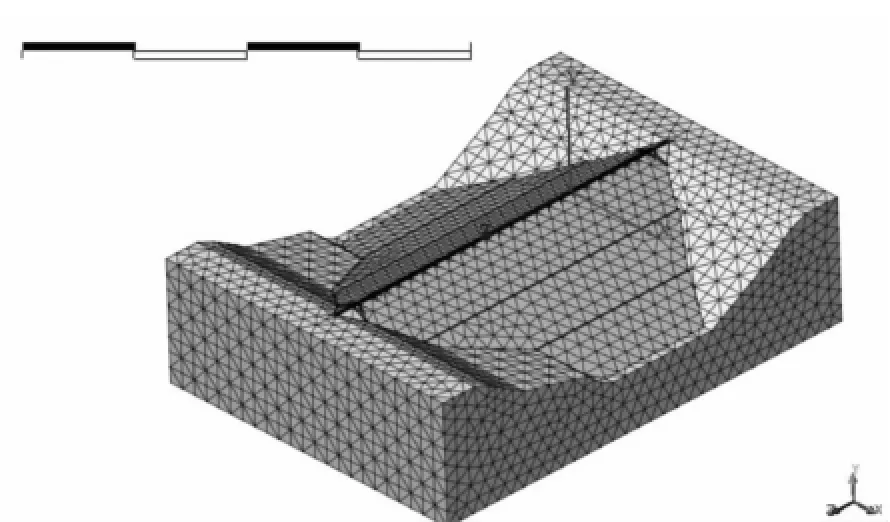
图4 坝体三维有限元模型
计算模型仍选用“E-υ模型”,计算时选取坝体最大断面。计算工况选取正常蓄水位与校核洪水位两种工况。防渗墙墙体材料采用低弹模混凝土,为作对比,混凝土弹性模量仍然分别取1 000 MPa、1 500 MPa、2 000MPa、2500MPa、3000MPa、5000MPa、8000MPa。
一般混凝土(弹模取值30000 MPa)和低弹模混凝土(弹模取值1000 MPa)在校核洪水位下位移见图5,防渗墙应力计算结果见表4和图6。

图5 校核洪水位下位移等值线图

表4 Midas/GTS应力应变计算成果表MPa

图6 弹性模量与最大压(拉)应力关系曲线
4 结论
(1)防渗墙墙体材料采用低弹模混凝土,具有较低的弹性模量更能适应不均匀受力及相应的变形。
(2)通过正常蓄水位(122.50 m)和校核洪水位(125.12 m)计算结果对比可见,水位的增加对墙体的应力有一定影响,水位升高会使墙体应力变大。
(3)另外,随着防渗墙弹性模量改变,防渗墙的应力随之变化。从本工程实例来看,弹性模量超过3 000 MPa以后,防渗墙的应力变化较为显著,建议弹性模量不超过3 000 MPa。
(4)本工程实例中的弹模取值是在特定的边界条件下计算得出的相关建议,实际上防渗墙的应力应变情况与坝高、温度、水位、坝体材料等多种因素有关,故在类似低弹模混凝土防渗墙施工前,必须通过应力计算得出弹性模量的临界值以保证防渗墙的安全性。
[1]白永年.中国堤坝防渗加固新技术[M].北京:中国水利水电出版社,2001.
[2]丁树云,蔡正银.土石坝渗流研究综述[J].人民长江,2008,39(2):33-36.
[3]尉高洋.低弹模混凝土防渗墙在某土石坝加固中的应用[J].浙江水利科技,2006,144(2):37-39.
[4]郎小燕.混凝土防渗墙在土石坝工程中的应用与发展[J].水利水电技术,2007,38(8):42-45.
2016-12-09)
罗东翔(1982-),男,满族,大学本科,工程师,主要从事水利水电工程管理,长距离输水等方面的技术性工作,通信地址:沈阳市和平区光荣街十四纬路,邮编110003,手机:15214216353,E-mail:7387333@qq.com。
