与圆锥曲线离心率有关的问题探究
2017-03-24河南省沈丘县第一高级中学赵继勇
☉河南省沈丘县第一高级中学 赵继勇
与圆锥曲线离心率有关的问题探究
☉河南省沈丘县第一高级中学 赵继勇
与圆锥曲线离心率有关的问题一直是高考的热点,圆锥曲线的离心率问题的解法有多种,如果我们能抓住关键,掌握规律,就能轻松、快速地解决相关问题,那么,关键是什么呢?规律又有哪些呢?下面笔者结合几类问题探讨一下有关解题策略.
一、与离心率有关的取值范围的研究
这类题目的解法,常常是利用已知条件直接构造不等式:利用圆锥曲线的范围及最值构造不等式;数形结合借助平面几何知识构造不等式;利用判别式、均值不等式或其他基本不等式来构造不等式;利用函数的单调性构造不等式.
分析:此题可以根据圆锥曲线的自身性质求离心率的取值范围.
解法一(数形结合法):设P的坐标为(x0,y0),
解法二(直接法):设P的坐标为(x0,y0),由代入椭圆方程b2x2+a2y2=a2b2,得
解法四(焦半径法):设∠F1PF2=α,点P(x0,y0).
由焦半径公式得|PF1|=a+ex0,|PF2|=a-ex0.
由余弦定理得|PF1|2+|PF2|2-2|PF1|·|PF2|cosα=|F1F2|2.
解法五(均值不等式法):由余弦定理得|PF1|2+|PF2|2-,得|PF1||PF2|cosα=c2,代入上式得|PF1|2+|PF2|2=6c2.
由椭圆定义得|PF1|+|PF2|=2a,根据均值不等式
又因为|PF1|·|PF2|≤a2-c2,c2≤a2-c2,c2≤3a2,
关键是找到含有a,b,c(或a,b,c中的两个)的一个不等式,可借助图形、圆锥曲线定义或常见结论等知识寻求解决问题的突破口.
解:如图1,设椭圆的左焦点为F1,半焦距为c,连接AF1,BF1,则四边形AF1BF为平行四边形,所以|AF1|+|BF1|= |AF|+|BF|=4.根据椭圆定义知,|AF1|+|AF|+|BF1|+|BF|=4a,所以4a=8,得a=2.因为点M到直线l的距离不小于,所以b2≥ 1,即a2-c2≥1,4-c2≥1,得所以椭圆的离心率的取值范围为

图1
点评:此题重点考查考生的等价转化与化归的能力,由|AF|+|BF|=4是否能等价转化为4a=8,另一方面草图对解题有不可轻视的指导引领作用.
二、离心率的值
解这类题的关键是:寻求建立a、b、c(或a、b、c中的两个)的一个等式或不等式;从“形”入手,从“数”下手;从圆锥曲线的定义思考,从几何图形的性质出发,从方程(或不等式)的角度落笔;结合平面几何基础知识,平面向量的知识,三角函数,柯西不等式,并充分利用数形结合的思想、方程思想、函数思想、等价转化思想、分类讨论的思想.
根据题目给定的条件,寻找并建立含有a,b,c(或a,b,c中的两个)的一个等式,即可求得离心率.
例3平面直角坐标系xOy中,双曲线C1:(a>0,b>0)的渐近线与抛物线C2:x2=2py(p>0)交于O,A,B.若△OAB的垂心为C2的焦点,则C1的离心率为________.
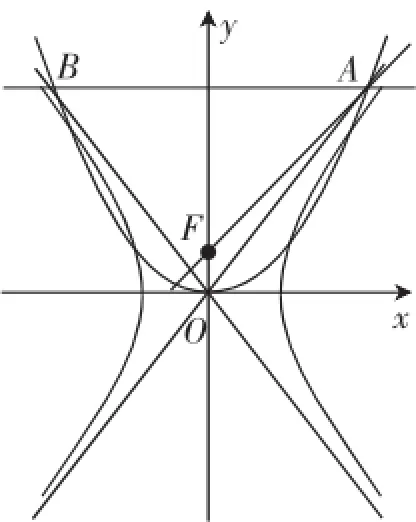
图2
因为F是△ABC的垂心,所以kOB·kAF=-1.
点评:(1)画图很重要,不画图做对题,那是不可能的,所以要做题得先画图.
(2)若题目较复杂,则需要耐住性子,要清醒地认识到:题易,我易,他易,不大意;题难,我难,他难,不畏难.此题图形有点复杂,但关键是要找到关于a、b、c(或a、b、c中的两个)的一个等式,沉着冷静,胆大心细,足以应对.
三、与离心率交汇的其他问题
这类问题要注意全方位,多角度去思考,寻求多方着力,尽可能通过分析推理得出最简便的方法.
例4已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且则椭圆和双曲线的离心率的倒数之和的最大值为().
解法一:如图3,设|PF1|=r1,|PF2|=r2,r1>r2,|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆与双曲线的离心率分别为e1,e2.
即4c2=+rr.12
又根据定义知,r1+r2=2a1,r1-r2=2a2,
得r1=a1+a2,r2=a1-a2,
解法二:如图3,设|PF1|= r1,|PF2|=r2,r1>r2,|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2;椭圆与双曲线的离心率分别为e1,e2.
由定义得r1+r2=2a1,r1-r2= 2a2,平方得.又由余弦定理得柯西不等式得
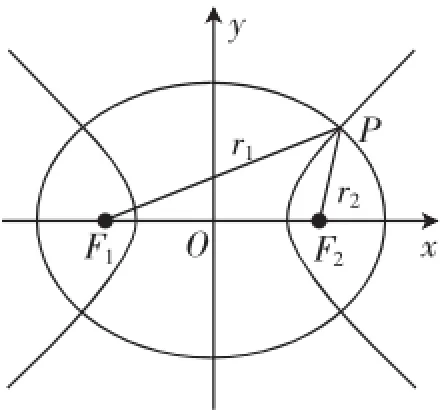
图3
解法三:设|PF1|=r1,|PF2|=r2,r1>r2,|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆与双曲线的离心率分别为e1,e2.
由余弦定理得4c2=-r1r2=(r1+r2)2-3r1r2=4-3r1r2,
消去r1,r2,得以下同解法二.
解法四:设|PF1|=r1,|PF2|=r2,r1>r2,|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆与双曲线的离心率分别为e1,e2.
解法五:设|PF1|=r1,|PF2|=r2,r1>r2,|F1F2|=2c,椭圆的长半轴长为a1,短半轴长为b1;双曲线的实半轴长为a2,虚半轴长为b2;椭圆与双曲线的离心率分别为e1,e2.
以“形”入手,借助函数、柯西不等式、三角函数、焦点三角形面积公式等,都是为了有效地架起已知与求解之间的桥梁,意在考查考生利用知识等价转化问题和解决问题的能力.
