超临界二氧化碳萃取藿香梗浸膏最佳工艺条件的数学模型

白凌，刘忠礼

（北京联合大学生物化学工程学院，北京 100023）

超临界二氧化碳萃取藿香梗浸膏最佳工艺条件的数学模型

白凌，刘忠礼

（北京联合大学生物化学工程学院，北京 100023）

通过运用超临界二氧化碳萃取技术萃取藿香梗浸膏，考察萃取时间、CO2流量、萃取温度以及萃取压力这4个因素对藿香梗浸膏萃取率的影响。对这4个因素分别进行多次单因素试验，用单因素试验数据结果进行相关正交试验并得到相应试验数据。利用统计学方法和数学试验软件，对单因素试验数据和相关正交试验数据进行多元二次多项式函数拟合，并对每次拟合结果进行数据分析以便对下一次数学实验中的变量因子进行取舍，经过多次二次多项式函数拟合，最终得到以萃取时间、CO2流量、萃取温度以及萃取压力这4个因素为变量的萃取率的最佳二次多项式函数模型，利用这个多元二次多项式函数模型计算出超临界二氧化碳萃取藿香梗浸膏的最佳工艺条件和相应萃取率。

超临界二氧化碳萃取；藿香梗浸膏；多元多项式；拟合；最佳工艺条件

超临界二氧化碳萃取技术［1－4］在天然香料的加工中得到了越来越广泛的应用。将该技术运用到藿香梗浸膏萃取中，考察萃取时间、CO2流量、萃取温度以及萃取压力这四个因素对萃取率的影响。利用单因素试验和相关正交试验得到相应的实验数据，再对这些数据进行多项式拟合和数据分析，进而得到上述四因素为变量的萃取率函数模型，最后利用该数学模型计算出最佳工艺条件［5－7］。

1 实验［8］

把150g藿香梗粉放在1L的萃取罐中密封。设定分离一的压力是7MPa、温度是55℃；设定分离二的压力是5MPa、温度是50℃。在萃取温度上升到设定温度后开始进行实验，实验结束后，用分离一及分离二所得产物的总和来计算产率。

2 结果与分析

2.1 萃取压力对萃取率的影响

设定萃取温度为40℃，CO2流量为40L/h，萃取时间为3h，改变萃取压力，观察藿香梗浸膏萃取率随萃取压力变化的情况。萃取压力对萃取率的影响见表1。

表1 萃取压力对萃取率的影响Table 1Effect of extracting pressure on extracting rate

由表1可知，萃取压力15MPa时萃取率较高。

2.2 萃取温度对萃取率的影响

设定萃取压力为15MPa，CO2流量为40L/h，萃取时间为3h，改变萃取温度，观察藿香梗浸膏萃取率随萃取温度变化的情况。萃取温度对萃取率的影响见表2。

表2 萃取温度对萃取率的影响Table 2Effect of extracting temperature on extracting rate

由表2可知，萃取温度42℃时藿香梗的萃取率较高。

2.3 CO2流量对萃取率的影响

设定萃取压力为15MPa，萃取温度为42℃，萃取时间为3h，改变CO2流量，观察藿香梗浸膏萃取率随超临界CO2流量变化的情况。CO2流量对萃取率的影响见表3。

表3 二氧化碳流量对萃取率的影响Table 3Effect of CO2flow rate on extracting rate

由表3可知，CO2流量40L/h时萃取率较高。

2.4 萃取时间对萃取率的影响

设定萃取压力为20MPa，萃取温度为45℃，CO2流量为35L/h，改变萃取时间，观察藿香梗浸膏萃取率随萃取时间变化的情况。萃取时间对萃取率的影响见表4。

表4 萃取时间对萃取率的影响Table 4Effect of extracting time on extracting rate

由表4可知，萃取时间越长，藿香梗浸膏的萃取率越高，考虑到实际生产中的经济因素，3h为合适的萃取时间。

2.5 超临界二氧化碳萃取藿香梗浸膏正交试验

上述四组单因素试验使我们得到了相对较佳的单因素试验条件。在此较佳的单因素试验条件下，我们设计以下四因素三水平正交试验，以确定上述四个因素对藿香梗浸膏萃取率的影响以及各个因素之间的交互作用。因素水平见表5，正交试验结果见表6。

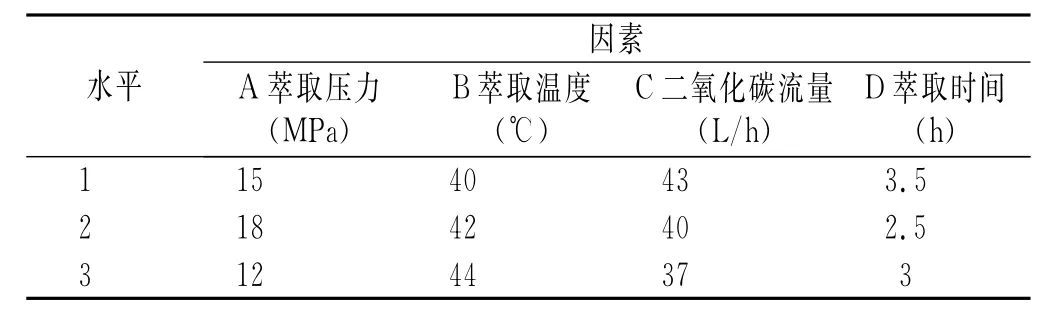
表5 超临界二氧化碳萃取藿香梗浸膏正交试验的四因素三水平表Table 5Four factors and three levels table of orthogonal experiments for the patchouli stem extract extracted with supercritical carbon dioxide fluid

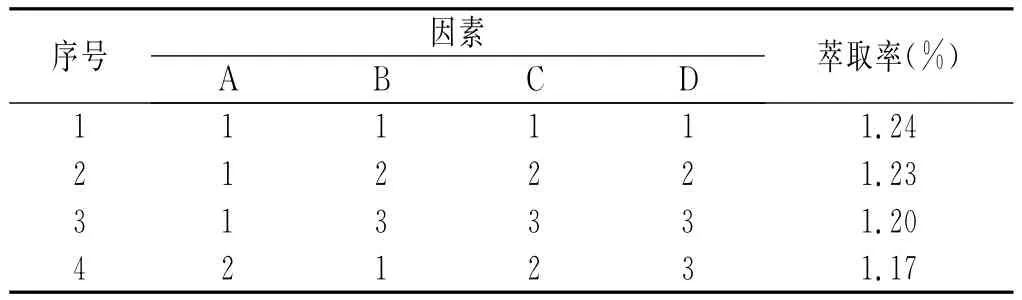
表6 超临界二氧化碳萃取藿香梗浸膏正交试验结果Table 6The results of orthogonal experiments for the patchouli stem extract extracted with supercritical carbon dioxide fluid

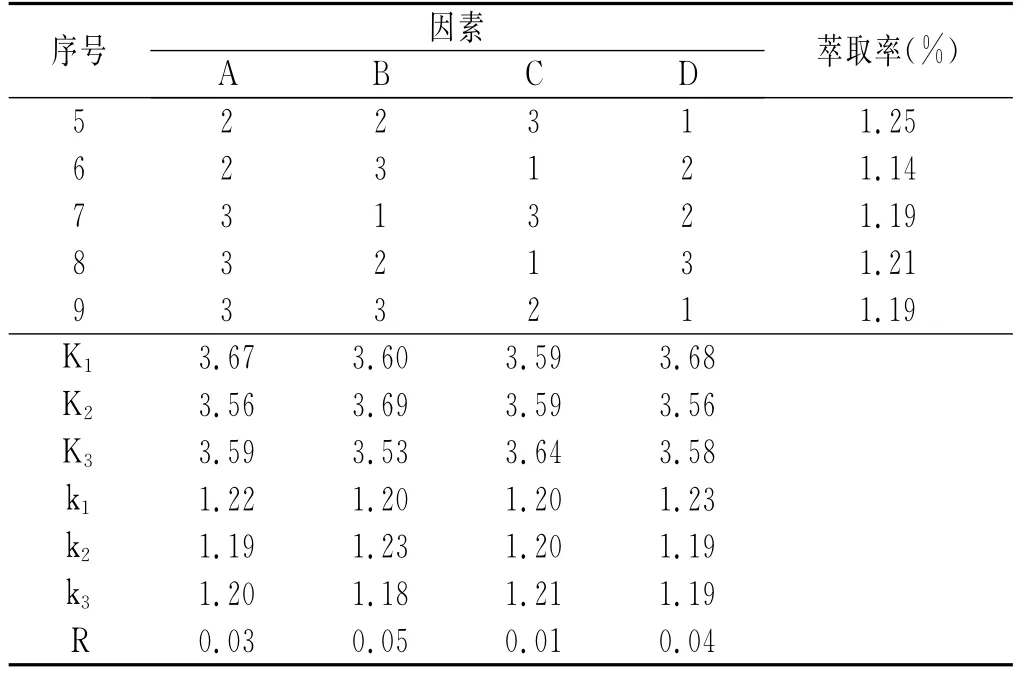
续表

由表5和表6可知，在以上四个因素中，萃取率受萃取温度的变化影响相对较大，而受CO2流量变化的影响相对较小。

3 数学建模

根据上述单因素试验以及正交试验结果，我们将四个因素对萃取率的影响简化为四元多项式模型：

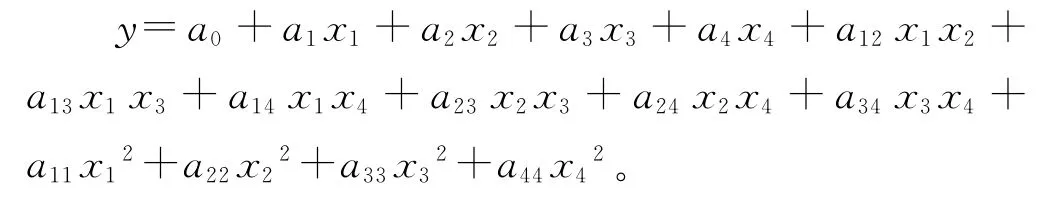
其中x1表示萃取压力（MPa），x2表示萃取温度（℃），x3表示CO2流量（L/h），x4表示萃取时间（h），y表示萃取率，ak，aij是待定系数（k＝0，1，2，3，4；i，j＝1，2，3，4；i≤j）。

3.1 完全二次多项式和交叉二次多项式拟合

设显著性水平为0.1，对上述实验数据进行完全二次型拟合，拟合结果见表7。

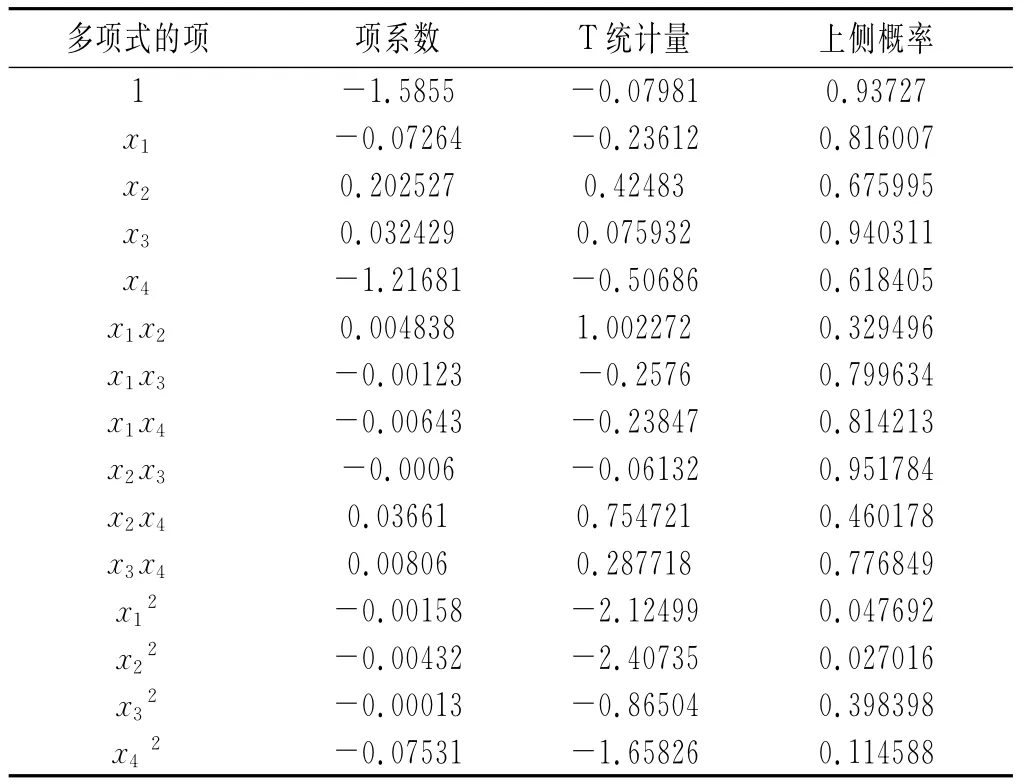
表7 完全二次多项式拟合结果Table 7Fitting results of complete quadratic polynomial

由表7可知，只有x12，x22两项的系数落入否定域，这说明纯二次项对萃取率y的影响较大；其余13项的系数都没有落入否定域，说明这些项对萃取率y的影响不大。造成这种结果的原因可能是因为拟合过程中含有交叉项。为了验证以上猜想，我们将拟合类型改为包含常数项，一次项和二次交叉项的二次多项式，拟合结果见表8。

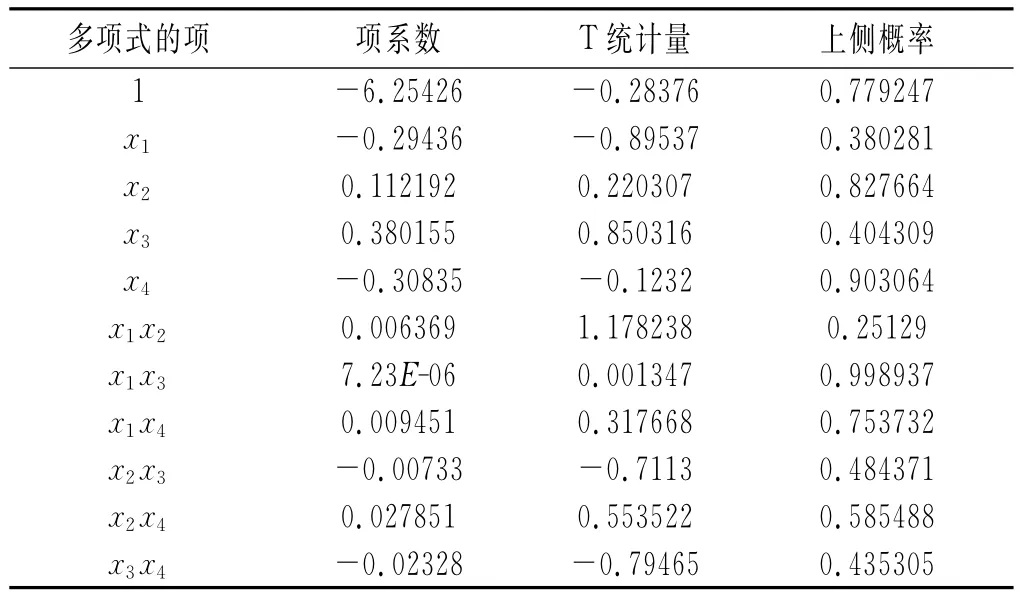
表8 交叉二次多项式拟合结果Table 8Fitting results of cross quadratic polynomial

由表8可知，以上11个系数都没有落入否定域，拟合结果相当病态。这证实了纯二次项是对萃取率y有显著影响的因子。下一步我们将在拟合模型中加入纯二次项并去掉对萃取率影响不显著的二次交叉项，进行纯粹二次多项式拟合。

3.2 纯粹二次多项式拟合以及特殊的纯粹二次多项式拟合

纯粹二次多项式拟合结果见表9。

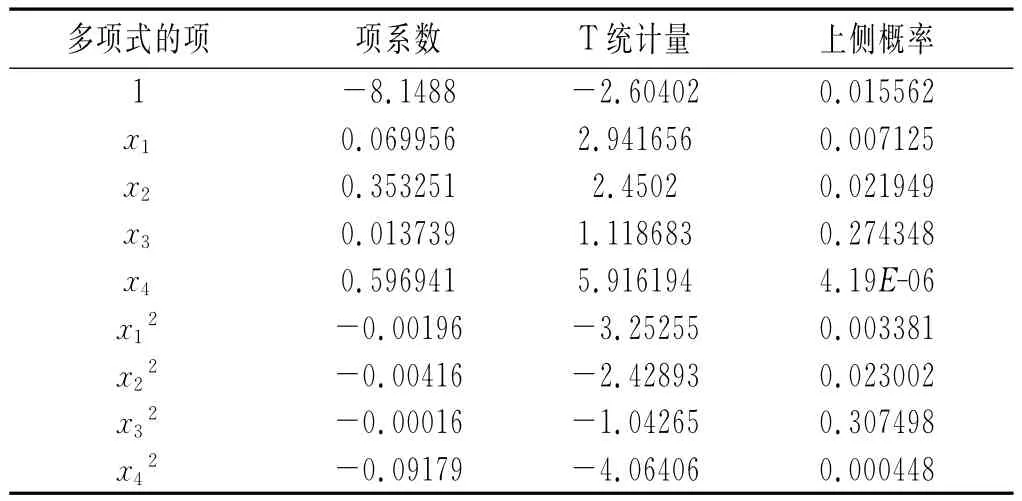
表9 纯粹二次多项式拟合结果Table 9Fitting results of pure quadratic polynomial

由表9可知，纯粹二次多项式的9项系数中有7个落入否定域，只有x3和x32两项的系数没有落入否定域，这表明这两项对萃取率y的影响相对不显著。如果将x3和x32两项同时从纯粹二次多项式中去掉，那么二氧化碳流量x3这个因子将在拟合多项式中消失，萃取率将不受其影响。因此，下面将考虑没有x3的纯粹二次多项式拟合（见表10）以及没有x32的纯粹二次多项式拟合（见表11）。

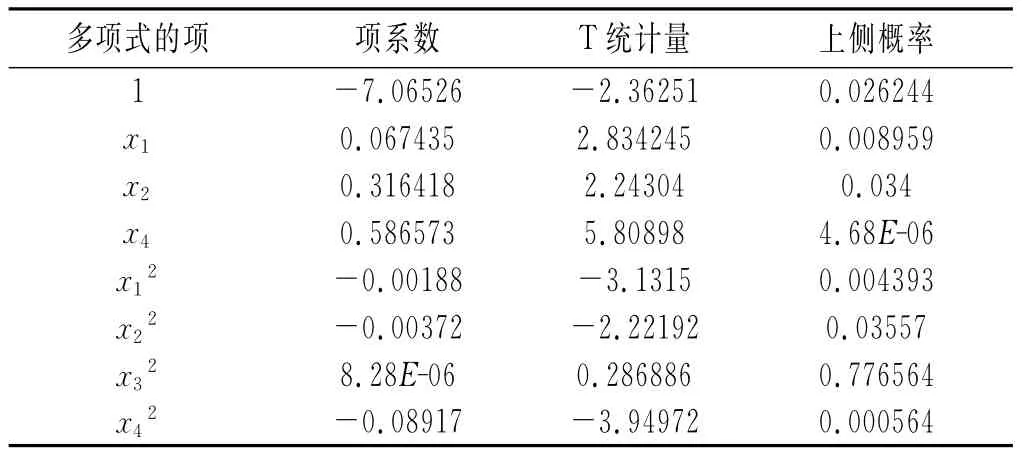
表10 不含x3项的纯粹二次多项式拟合结果Table 10Fitting results of pure quadratic polynomial excludingx3

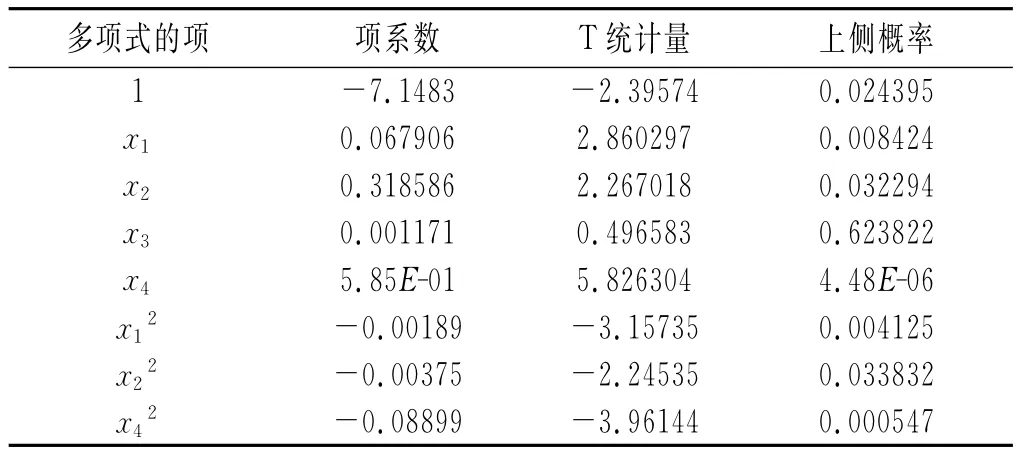
表11 不含x32项的纯粹二次多项式拟合结果Table 11Fitting results of pure quadratic polynomial excludingx32

在表10中，x32的系数没有落入否定域；而在表11中，x3的系数没有落入否定域中。这可能是由于我们在拟合过程中忽略了与x3相关的二次交叉项。因此，在纯粹二次多项式拟合中分别加入x1x3，x2x3，x4x3项，经过多次拟合实验，可以发现将拟合模型设定为包含所有常数项、所有一次项、x2x3一个二次交叉项以及x12，x22，x423个二次项的多项式时，拟合结果最佳，拟合结果见表12。

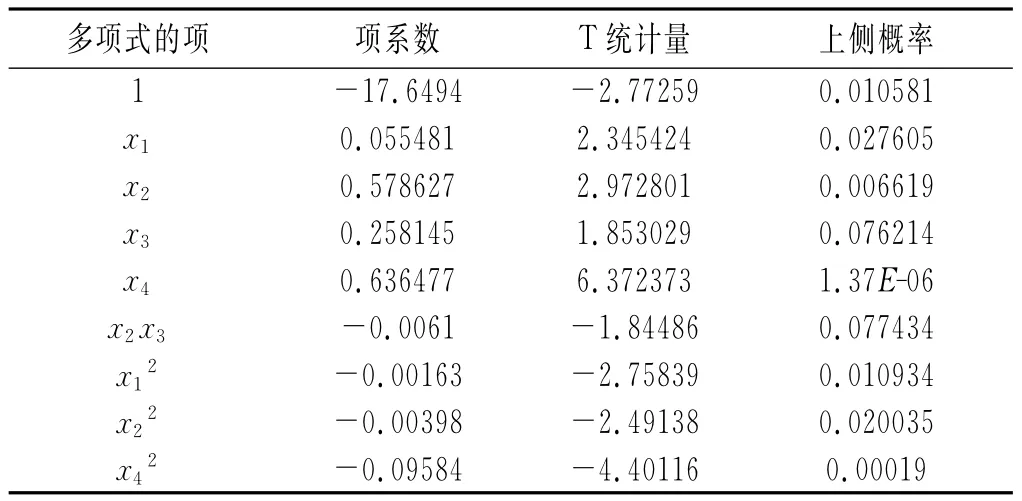
表12 含有x2x3但不含x32项的纯粹二次多项式拟合结果Table 12Fitting results of pure quadratic polynomial excludingx32and includingx2x3

由表12可知，多项式系数全部落入否定域中，说明这9项对萃取率y的影响都很显著，拟合结果非常理想，由此可以断定含有x2x3但不含x32项的纯粹二次多项式是较为合理的数学模型。

3.3 二次多项式数学模型

对含有x2x3但不含x32项的纯粹二次多项式进行拟合可信度的F检验得到F（8，24）的值为17.09517，上侧概率值为3.57586e-08，拟合可信度较高。从而得到萃取压力、萃取温度、CO2流量以及萃取时间这4个因素对萃取率的影响较为合理、含有x2x3但不含x32项纯粹二次多项式数学模型。

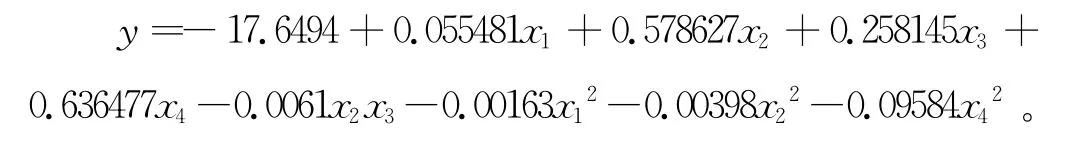
4 结论

利用超临界二氧化碳萃取技术，根据单因素试验和相关正交试验的试验数据，应用统计学方法对试验数据进行多项式拟合和数据分析，建立了关于藿香梗浸膏萃取率的四元二次多项式函数，从而进一步得到获取最佳萃取率的工艺条件：当萃取压力为17.0117MPa、萃取温度为48℃、CO2流量为20L/h、萃取时间为3.2h时，产率最大，最大产率为1.7905%。

［1］葛保胜，王秀道.超临界CO2萃取大蒜提取物的研究［J］.中国调味品，2003（4）：17-19.

［2］白凌，刘桂清，方全有.超临界二氧化碳萃取藿香叶浸膏的数学模型［J］.中国调味品，2013，38（2）：43-46.

［3］张小利，刘烈淼.超临界CO2提取细叶韭花香精油的工艺研究［J］.中国调味品，2012，37（6）：74-78.

［4］王雪飞，赵晶，那治国.超临界CO2萃取红辣素的研究［J］.中国调味品，2008，33（10）：66-69.

［5］费浦生，羿旭明.数学建模及其基础知识详解［M］.武汉：武汉大学出版社，2006：86-88.

［6］薛定宇，陈阳泉.高等应用数学问题的MATLAB求解（第二版）［M］.北京：清华大学出版社，2008：291-293.

［7］茆诗松，程依明.概率论与数理统计教程［M］.上海：高等教育出版社，2011：286-290.

［8］刘玉平，孙宝国，石华治，等.超临界二氧化碳萃取藿香梗和藿香叶浸膏的工艺研究［J］.化工学报，2008（3）：791-795.

The Mathematical Model of the Optimal Technological Conditions for Extraction of the Patchouli Stem Extract by Supercritical Carbon Dioxide Fluid

BAI Ling，LIU Zhong-li
（College of Biochemical Engineering，Beijing Union University，Beijing 100023，China）

The effects of extracting pressure，extracting temperature，extracting time and CO2flow rate on the process of patchouli stem extract by supercritical carbon dioxide fluid are investigated.Single factor experiment and orthogonal experiment are designed for four factors respectively.The corresponding experiments data have been used to fit multiple polynomials，and the variables in the polynomials have been estimated to decide whether delete or not.The optimal multiple polynomials model has been obtained by mathematical experiments which uses extraction time，CO2flow，extraction temperature and extraction pressure as variables，and the optimal technological conditions of extraction can be computed.

supercritical carbon dioxide fluid extraction；patchouli stem extract；multiple polynomial；fitting；the optimal technological conditions

TS201.1

A

10.3969/j.issn.1000-9973.2017.03.005

1000-9973（2017）03-0018-04

2016－09－25

北京市教育委员会科技计划面上资助项目（KM201511417012）

白凌（1981－），女，讲师，硕士，研究方向：数学与应用数学；

刘忠礼（1971－），男，副教授，硕士，研究方向：数学与应用数学。