基于聚类系数的链路预测算法改进
2017-03-24李星陶汉
李星+陶汉


摘要: 链路预测是指通过已知的网络信息来预测网络中的丢失边信息或者是错误连边信息,链路预测是对于网络分析和数据挖掘的一项支撑学科。经过数十年的学科发展,链路预测得到了长足的发展,大量新的预测算法得以提出。本文提出了一种基于网络节点中聚类系数的算法优化思路,并将该优化思路运用到9种经典的算法上,在5种真实数据集上的实验表明了该优化思路的可行性。链路预测的准确性研究多基于丢失边的预测,对于错误连边的准确性预测少有涉及,本文的实验部分同时涉及了丢失边的预测以及错误连边的预测。传统的链路预测比较实验,对于测试集多选取10%这一固定值,本文为了说明算法的健壮性,针对不同大小的测试集进行了广泛的实验。
关键词:复杂网络;链路预测;聚类系数;错边识别;局部相似性
中图分类号:TP391 文献标识码:A 文章编号:1009-3044(2017)01-0239-05
Abstract: Link prediction is a subject which uses the current network information to predict the missing and spurious links, so it is a supporting discipline for network analysis and data mining. After decades of academic development, link prediction has achieve a lot of progress, a large number of algorithms have been proposed. In this paper, we have proposed an optimization thought which was inspired by clustering coefficient. We have applied this optimization methods to nine kinds of classical algorithms, results on five real data sets prove the feasibility of the optimization method. Former study on link prediction mainly focus on the prediction of missing links, while in this paper we have also concern the spurious links. Compared with the traditional research, we have doing experiments on varies ratio of training set, previous training set were fixed at 10% for the most conditions.
Key words: complex networks; link prediction; clustering coefficient; spurious links; local similarity
1 概述
关于网络结构的研究已有数百年的历史,网络学科的理论发展经过了规则网络,随机网络和复杂网络三个阶段。网络上的首项研究可以追溯到1736年欧拉关于哥尼斯堡七桥问题的提出与解决,这属于规则网络时代的研究。之后的很长一段时间,网络学科都没有很大的发展。1959年,匈牙利的著名数学家Erd?s和Rényi建立了著名的随机图(ER)理论,这才将网络研究带入到了第二个阶段[1]。随机网络的提出将网络的理论研究拓展到了更为广泛的科研领域,比如社会学家也可以利用随机理论对于人类关系网络进行建模。复杂网络的开启主要归功于Watts和Strogatz在1998提出的小世界模型以及Barabási 在1999提出的无标度网络[2,3]。小世界网络指网络中大多数的节点不直接相连,但彼此之间只需通过少量节点即可以到达,即“六度分离”理论的诠释。无标度网络指网络中节点度的分布符合幂指数,即少数的节点具有很高的度分布而大多数节点的度相对较低。
近年来,随着复杂网络学科的快速发展,作为其分支之一的链路预测研究也得到了越来越广泛的关注。网络中的链路预测是指根据网络现有的节点属性以及网络拓扑等信息来预测网络中尚未产生连边的两个节点之间产生链接的可能性[4]。链路预测包含了对于未知边的发掘以及网络演化中即將产生的边的预测。链路预测很好地将网络与信息科学进行了连接,可以很好地处理信息科学中缺失信息的还原与预测。
链路预测具有重要的实践以及理论价值[5,6,7]。人类已知的蛋白质相互作用网络只占真实网络的冰山一角,很多蛋白质之间是否有相互作用需要大量的实验来验证。酵母细菌的相互作用网络已被观察到的只有20%,人类网络更是只有0.3%。由于验证蛋白质相互网络将消耗巨大的人力以及时间的成本,所以如果能用链路预测的方式对可能存在的边进行预测,进而指导实验,将对于人类的生命工程产生巨大的推动作用。社交网络中也存在信息丢失的情况。比如QQ当中,我们好友列表中并不能涵盖我们全部的好友信息。链路预测此时便可以根据现有好友列表向我们进行推荐可能认识的好友,进一步完善我们的好友列表 以及增强用户对于产品的忠诚度。同样的道理,链路预测的算法也可以在商品推荐中得以应用。链路预测的理论价值主要在于帮助我们更好的认识网络的演化机制。针对某种或某类网络,有许多模型都提供了可能的演化机制,但由于刻画网络性质的统计变量很多,所以很难比较哪种演化机制更好。有了链路预测,我们便得到了一个统一量化的指标,利用该演化机制构建链路预测的算法,算法预测准确率高者更符合网络的演化,从而分析哪一个机制能够更好的刻画网络的演化,这大大推进了网络演化机制的研究工作。
早期的链路预测主要基于机器学习和马尔科夫链。该类方法虽然具有较高的预测准确率,但较高的时间复杂度限制了被预测网络的规模。同时,由于该类方法的分类往往需要获取节点的属性信息,节点的属性信息往往很难获取即使获取节点信息也未必能保证信息的可靠性。比如在社交网络之中,用户的年龄、性别、住址未必会如实填写,这便给该类基于节点属性的算法造成了很大的障碍。由于基于马尔科夫以及机器学习方法的弊端,最近几年的链路预测更多转移到了利用网络的拓扑信息进行预测。利用网络结构进行预测的方法主要分为基于相似性的链路预测和基于似然分析的链路预测。基于相似性的链路预测的前提假设是,如果两个点越相似那么这两个点存在连边的可能性越大。相比较基于相似性的链路预测,基于思然分析的链路预测是一种更为復杂的框架,虽然可以取得较高的准确率,但同基于机器学习的方法类似,当网络节点数目达到数千个之时,算法处理起来之时便会感到吃力。考虑到计算的复杂度以及通用性,本文所提出的算法可以归纳到基于相似性的链路预测框架之内[8,9,10,11]。
在本文中,我们提出了利用网络节点的聚类系数这一特征来提升基于相似性的链路预测算法的准确性这一思路。我们将聚类系数这一特征引入到了9个经典的链路预测算法之中并得到了9种新的链路预测算法,对此我们在5个真实的数据集之上进行了实验,实验表明算法中聚类系数的引入可以在一定程度上提升网络的预测准确性。由于过往链路预测的研究d多数只会进行丢失边的实验[12,13],在此基础上本文还添加了算法对于错误边纠错能力的实验,实验表明了我们新的算法在网络噪声纠错能力上的提升。除此之外,过往研究将测试集的比例固定在10%这一值之上,我们对此进行了扩展,我们将测试集的比例伸展到了4%到20%范围之间,进一步提升了实验的完整性,这一范围的变化也验证了我们算法的健壮性。
2 问题描述
定义G(V, E)为一个无向网络,其中V为节点集合,E为边集合。网络总的节点数为N,边数为E。若该网络为一个全连通网络,那么该网络共有N(N ?1)/ 2条边,即全集U。给定某个链路预测算法,该算法会对每对没有连边的节点对(x,y)进行评分,赋予一个分数值Sxy。将所有未连接的边进行评分,分数高的边出现的概率大[14]。
关于丢失边和错误连边的预测稍有不同,下面对他们进行分别描述:
2.1 丢失边的预测
为了预测算法的准确性,一般会将网络中的边划分为两个部分:训练集ET和测试集EP。显然,ETEP=E,且ETEP=?。我们将属于U但不属于E的边称作不存在的边。在对算法进行准确度的测试时,我们只会利用到训练集中的信息,即ET。
2.2 错误边的预测
为了预测算法对错误连边的识别率,我们将在现有网络的基础上增加一些连边来模拟网络中包含错误连边的情况。现有网络中的边我们表示为E, 我们向网络中添加的不存在的边为EP,ET=EP+E, 在对算法进行准确度的测试时,我们同样只会利用到训练集中的信息,即ET。
3 数据集划分
为了测试特定链路预测算法的准确性,我们需要从网络之中选取一部分作为测试集,剩余部分作为训练集。不同的测试集的选取方法会对实验结果造成一定程度上的影响[15]。常见的测试集的选取方式主要有随机抽取、逐项遍历、k-折叠交叉实验、滚雪球抽样、熟识者抽样、随机游走抽样、基于路径抽样这7种。本文中采取最为常用的随机抽样法。对于数据集的划分,丢失边的预测和错误边的预测稍有区别。
3.1 丢失边的预测
给定的网络G中含有N个节点E条边,现给定某一测试集的选取比例p,我们将等概率的从E条边中选取p*E(若非整数,向上取整)条边构成测试集,E中的剩余边作为训练集。一般的链路预测试验中p的选取比例为10%,为了验证本文算法的健壮性,我们将p设置为 [0.04,0.08,0.12,0.16,0.20] 这五个不同的值。
3.2 错边的识别能力
若网络G中含有E条边,先给定某一测试集的选取比例,即错误边的比例。我们将等概率的从不存在的边中选取p*E(若非整数,向上取整)条边构成测试集EP,ET= E+EP。为了便于比较,我们p的选值范围与丢失边的情况相同。
4 经典算法
1) CN指标(Common Neighbors)[16]。对于节点x,Γ(x)表示x的邻居节点,同理Γ(y)表示y的邻居节点,下式表示的便是x节点和y节点的共同邻居数。该算法认为两个节点拥有越多的共同邻居数,越可能相连接。
2) Salton指标[17]。kx、ky分别表示节点x和节点y度的大小,salton指标也被人们称作余弦相似度指标。
3) Jaccard指标[18]。该指标是Jaccard一百多年前所提出来的
4) Sorensen指标[19]。该指标主要用于生态网络系统的预测。
5) 大度节点有利指标(hub promoted index, HPI)[20]。根据式子中的分母部分,我们知道该算法认为度较大的节点更有利于网络的连接。
6) 大度节点不利指标(hub depressed index, HDI)[10]。相比较于上式,该算法认为度较大的节点不利于网络的连接。
7) LHN指标[21]。与Sorensen指标类似,仅将分母元素的相加改为相乘。
8) AA指标(Adamic-Adar)[22]。这是对于CN指标的一种改进,该算法认为共同邻居中,度较小的更利于网络的连接。
9) RA指标(Resource Allocation)[10]。形式上类似于AA,但该算法是受到网络中资源分配模型的启发。
5 基于节点聚类系数的算法改进
5.1 聚类系数的定义
网络中节点的聚类系数由Watts和Strogatz在1998年所提出。针对网络中的某一个节点vi,其聚类系数定义为其邻居间的连边数量占可能连边的比例,数学表示为:
其中ki表示节点vi的度,li表示节点vi的ki个邻居之间的连边数量[23]。
聚类系数表示了节点邻居之间的连接紧密程度。在生活中,若将人类的生活抽象为社交网络,若某人的聚类系数较大,那么该人的朋友之间相互认识的可能性越大,那么我们认为该人的好友之间产生连边的概率较大。基于大的聚类系数促进网络的连接,所以本文认为可将聚类系数这一特征融入到现有算法之中,提升算法对于部分网络的预测准确度。
5.2 算法改进
对于以上提到的9種链路预测算法,加入节点的聚类系数这一特性之后,得到的改进算法如下所示:
6 实验分析
本章的实验部分,我们重点比较了9种经典的链路预测算法与我们改进后的9种算法,在5类真实的数据集之上我们不仅比较了丢失边预测的准确性同时比较了错误边的恢复效果。本章将对数据集,评价指教,实验结果三方面进行介绍。
6.1 实验数据
6.1.1 数据说明
本文实验中的数据是在pajek和stanford两个数据集当中收集而来。USAir表示的是美国的航线信息,节点表示机场,若两个机场之间有直达航线,那么该两点之间存在一条连接边。Elegans表示的是线虫的神经网络,节点表示线虫的神经元,突触或间隙表示为连边。Footbal数据中的节点代表国家队,这些国家中的球员频繁参加国外联赛,若国家队中有成员在另外一个国家的联赛中踢球,那么这两个国家队之间存在连边信息。Jazz表示jazz演奏家之间的合作网络。Karate是社会网络分析领域中的经典数据集,该网络构造了美国一所大学空手道俱乐部中34名成员的社会关系,若两人在现实之中是好友关系,那么该两人之间存在一条连边。
6.1.2 数据的特征统计
|V|代表网络中节点的数目。|E|代表网络中边的数目。D表示网络的密度,计算公式为。C表示节点的聚类系数,上文已经给出了计算公式。
6.2 评价指标
常见的链路预测算法的衡量指标有AUC(area under the receiver operating characteristic curve),Precision和Ranking Score三种。Precision考虑的是排在前K位的预测是否准确,Ranking Score侧重于所预测边的排序,AUC是三种当中最为常用的一种指标,他可以很好的从整体上衡量算法的准确度。
在丢失边的预测之中,每次从测试集和不存在的边当中分别取出一条边,链路预测算法根据训练集信息分别对两条边进行评分,如果测试集中边的评分大于不存在的边,那么加1,如果测试集中边的评分等于不存在的边,那么加0.5,如果测试集中边的评分大于不存在的边,那么加0。如此往复比较n次,若测试集中的边分值大于不存在的边的次数为n',测试集中的边分值等于不存在的边的次数为n''。
在错误边的预测中,每次从E和EP当中分别取出一条边,如果E中边的评分大于EP中的评分,那么加1,如果相等加0.5,否则加0。如此往复比较n次,若E中的边分值大于EP边的次数为n',等于的次数为n''。
根据先前的划分,网络中的未知边分为不存在的边和测试集当中的边。虽然测试集中的边被划分在了未知边中,但好的算法是应该可以区分出不存在的边和测试集当中的边的,即根据算法测试集中边出现的概率要高于不存在的边。现,那么AUC值的计算公式为:
显然,如果链路预测的算法不具备预测能力, AUC=0.5。因此AUC大于0.5的程度衡量了算法在多大程度上比随机预测的方法精确。
6.3 实验结果
为了保证试验的准确定,当我们确定某一个p值之后,我们会对测试集进行100次划分,划分之间彼此不关联,这主要是防止测试集的随机性对试验结果造成的误差。测试集划分好之后,我们将内层循环次数确定为1000次,也就是说总循环比较的次数为100000次,该次数对应于上述AUC指标中的n。
以下便是实验的结果:
1) Elegans网络中缺失边的发现与错误边的纠正,左侧为缺失边的发现,右侧为错误边的纠正。下图中共18种算法进行比较,其中原算法9种,加入聚类系数改进后的算法9种。为了便于比较,我们将某一算法和改进后的算法一一对应,这主要体现在绘图时线段的颜色,如下图所示CN和加入聚类系数后的CCN算法均由黑色线段表示,RA和CRA均由红色表示。此外,原算法用虚线表示,改进后的算法用实线表示。结果图的横坐标表示所选取的训练集的比例p,纵坐标表示算法的预测准确度。
从Elegans的实验结果图可以看出改进后的算法相比较原算法在准确率上有所提升,该效果的提升不仅在于发现丢失边的情况同时适用于错误连边的纠正。随着测试集比例的提升,改进后的方法同样优于原算法。
2) Football网络的实验结果如下图所示。实验结果表明改进后的算法在整体上明显优于原先的算法,此外在链路预测的过程中我们发现当p=0.08时,预测的准确率达到最高值。
3) Jazz网络的实验结果如下图所示。改进后的算法只在少数几个点之上不能超越原算法,整体表现仍然十分优异。
4) USAir网络的实验结果如下图所示。该实验结果分层现象十分明显,改进后的算法曲线明显在改进前算法的曲线之上,这表明加入聚类系数这一节点的局部信息之后,该
9种算法在美国航空网络的预测上效果明显提升。
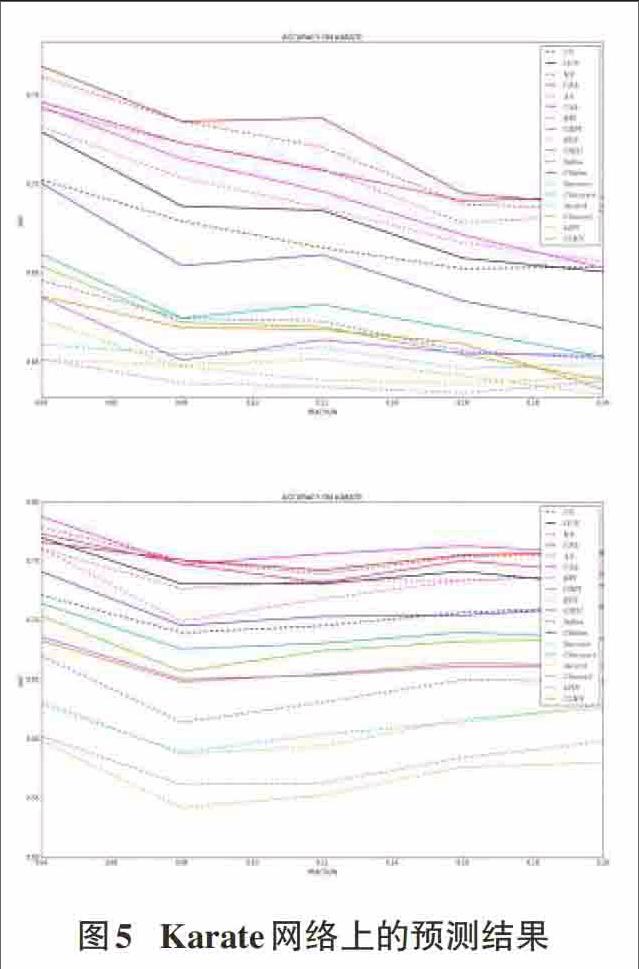
5) Karate网络的实验结果如下图所示。与上述四种网络结果共同验证了算法改进的有效性,此外我们发现这些链路预测算法对错误连边的发现要略优于预测不存在的边。
7 总结与展望
聚类系数表示节点邻居之间联系的紧密程度,较高的聚类系数表明邻居间较高的连接概率。受该指标的影响,我们将其特性添加到现有的9种链路预测算法之中得到了我们改进后的9种算法。通过在5种真实网络上的实验,我们发现了改进后的算法在这5种网络上有着更好的表现。除此之外,针对不同大小的训练集划分比例,我们进行了大量的比较实验,过往研究很少会探讨训练集p的大小对于实验结果的影响。我们发现不同大小的训练集对于实验结果会产生影响,但改进后的算法与原算法的相对大小不变。最后,我们的链路预测实验还包含了算法在错误连边上的发掘能力,实验表明,若我们有算法A、B,算法A相比B在丢失边的发掘能力上可能会更好,但若换做是错误边的发现,那么B算法可能会优于A算法。
本研究只简单地考虑了节点的聚类系数对于链路预测算法的影响,除此之外,在未来的研究当中我们可将更多的网络特征融入到算法之中来进行算法的提升。本次实验的网络只有5种,更多数据的实验有待补充,我们不排除特定网络之上,改进后算法的准确率不如原算法。本次实验网络的节点只有几百个,更大规模网络的链路预测研究有待进一步深入。
参考文献:
[1] Erd?s P, Rényi A. On Random Graphs[J]. Publicationes Mathematicae, 1959, 6:290-291.
[2] Watts D J, Strogatz S H. Collective dynamics of ‘small-worldnetworks[J]. nature, 1998, 393(6684): 440-442.
[3] Barabási A L, Albert R. Emergence of scaling in random networks[J]. science, 1999, 286(5439): 509-512.
[4] Lü L, Zhou T. Link prediction in complex networks: A survey[J]. Physica A: Statistical Mechanics and its Applications, 2011, 390(6): 1150-1170.
[5] Gao F, Musial K, Cooper C, et al. Link prediction methods and their accuracy for different social networks and network metrics[J]. Scientific Programming, 2015, 2015: 1.
[6] Li D, Zhang Y, Xu Z, et al. Exploiting Information Diffusion Feature for Link Prediction in Sina Weibo[J]. Scientific reports, 2016, 6.
[7] 劉宏鲲, 吕琳媛, 周涛. 利用链路预测推断网络演化机制[J]. 中国科学: 物理学 力学 天文学, 2011, 41(7): 81.
[8] Lü L, Pan L, Zhou T, et al. Toward link predictability of complex networks[J]. Proceedings of the National Academy of Sciences, 2015, 112(8): 2325-2330.
[9] Chen B, Chen L. A link prediction algorithm based on ant colony optimization[J]. Applied Intelligence, 2014, 41(3): 694-708.
[10] Zhou T, Lü L, Zhang Y C. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623-630.
[11] Liu Z, Dong W, Fu Y. Local degree blocking model for link prediction in complex networks[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2015, 25(1): 013115.
[12] Guimerà R, Sales-Pardo M. Missing and spurious interactions and the reconstruction of complex networks[J]. Proceedings of the National Academy of Sciences, 2009, 106(52): 22073-22078.
[13] Zhang P, Wang X, Wang F, et al. Measuring the robustness of link prediction algorithms under noisy environment[J]. Scientific reports, 2016, 6.
[14] 吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5): 651-661.
[15] Zhu Y X, Lü L, Zhang Q M, et al. Uncovering missing links with cold ends[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(22): 5769-5778.
[16] Lorrain F, White H C. Structural equivalence of individuals in social networks[J]. The Journal of mathematical sociology, 1971, 1(1): 49-80.
[17] Salton G, McGill M J. Introduction to modern information retrieval[J]. 1986.
[18] Jaccard P. Etude comparative de la distribution florale dans une portion des Alpes et du Jura[M]. Impr. Corbaz, 1901.
[19] Sorensen T. {A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons}[J]. Biol. Skr., 1948(5): 1-34.
[20] Ravasz E, Somera A L, Mongru D A, et al. Hierarchical organization of modularity in metabolic networks[J]. science, 2002, 297(5586): 1551-1555.
[21] Leicht E A, Holme P, Newman M E J. Vertex similarity in networks[J]. Physical Review E, 2006, 73(2): 026120.
[22] Adamic L A, Adar E. Friends and neighbors on the web[J]. Social networks, 2003, 25(3): 211-230.
[23] 李建, 鄭晓艳. 复杂网络聚类算法综述[J]. 电脑知识与技术, 2015(5): 019.
