你犯类似的错误了吗？

王华军

同学们在学习“数据的收集、整理和描述”这一章时，常犯的错误有：

一、方法选择不当

例1 （2016·山西）以下问题不适合全面调查的是（ ）.

A.调查某班学生每周课前预习的时间

B.调查某中学在职教师的身体健康状况

C.调查全国中小学生课外阅读情况

D.调查某校篮球队员的身高

【错解】选A，因为每个学生每周课前预习的时间是个估计值，不准确，所以不适合全面调查.

【诊断】每个学生每周课前预习的时间不准确，是估计值，但不影响对该班学生每周课前预习时间的全面调查.同样，对某中学在职教师的身体健康状况和某校篮球队员身高的调查也适合全面调查.而全国中小学生课外阅读情况的调查人数多，工作量太大，且这种统计不需太精确，适合抽样调查.

【正解】选C.

【点评】本题考查抽样调查和普查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用.

二、概念模糊不清

例2 某校要了解七年级女生的身体状况，从七年级400名女生中抽出30名进行体重检测.在这个问题中，总体、个体、样本各是什么？样本容量是多少？

【错解】总体是七年级400名女生，个体是每个女生的身体状况，样本是抽取的30名女生，样本容量是30人.

【诊断】错解认为总体、个体、样本的考查对象不一样，且多余地给样本容量添加了单位.总体、个体、样本的考查对象在同一问题中应该是统一的.

【正解】总体是七年级400名女生的体重，个体是每个女生的体重，样本是抽取的30名女生的体重，样本容量是30.

【点评】对总体、个体、样本的考查，其考查对象应该是一样的，区别就在于考查范围的不同，所以解答此类题时，要先搞清楚考查对象是什么.样本容量指的是样本中个体的数目，没有单位.

三、对应关系不明

例3 省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动.某中学为了了解本校学生的上学方式，在全校范围内随机抽查了部分学生，将收集的数据绘制成如下两幅不完整的统计图（如图1和图2所示），请根据图中提供的信息，解答下列问题.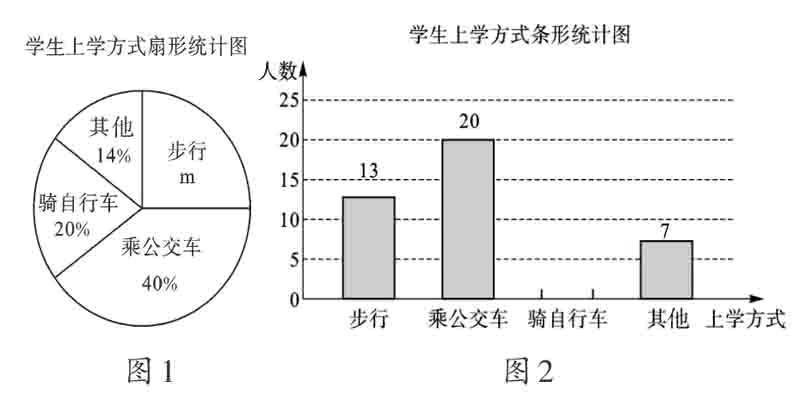

（1）m=_________，這次共抽取_________名学生进行调查，补全条形图；（2）在这次抽样调查中，采用哪种上学方式的人数最多？（3）如果该校共有1500名学生，请你估计该校骑自行车上学的学生约有多少名？

【错解】（1）m=26%，这次共抽取20÷20%=100（人）；（2）、（3）略.

【诊断】错解没有将条形统计图与扇形统计图结合起来看，出现了错误.条形统计图中乘公交车的20人应该与扇形统计图中乘公交车的40%对应.

【正解】（1）m=1-40%-20%-14%=26%，这次共抽取20÷40%=50（人），补充条形统计图如图3；（2）乘公交车上学的人数最多；（3）该校骑自行车上学的人数约为1500×20%=300（人）.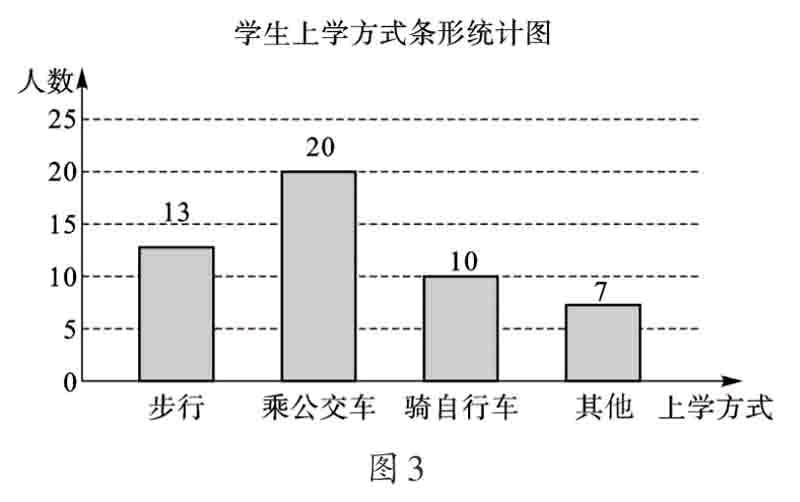

【点评】解决此类问题要准确地对统计图信息加以分析，会借助样本的特征来估计总体的相应特征.

四、公式理解不透

例4 为了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，可得频率分布表如下：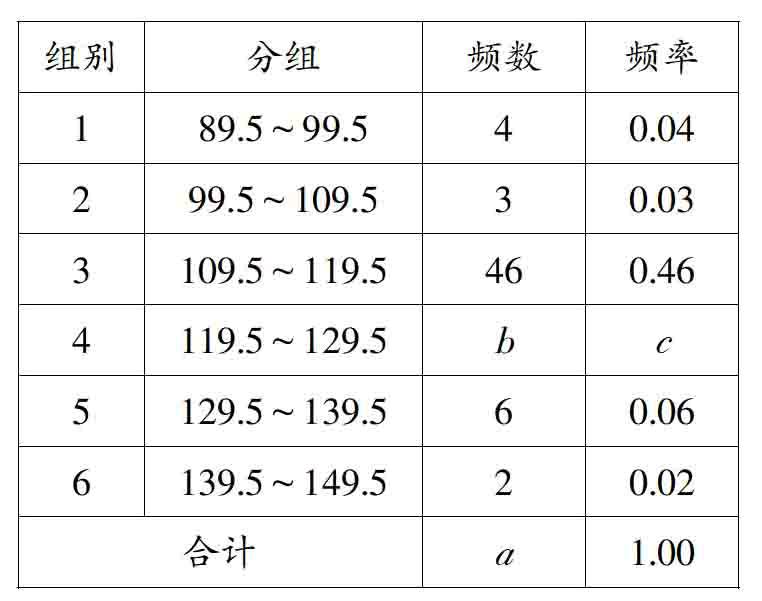

（1）这个问题中，总体是_________；

（2）a=_____，b=_____， c=_____；

（3）若次数在110次以上（含110次）为达标，试估计该校初三毕业生一分钟跳绳次数的达标率是多少？

【错解】（1）初三毕业生一分钟跳绳的次数90 ；（2）9，0.39；（3）略.

【诊断】错解对样本容量、频数、频率之间的关系理解不透，从而错误地求出了a、b、c的值.

【正解】（1）初三毕业生一分钟跳绳的次数 ；（2）a=4÷0.04=100，b=39，c=0.39；（3）跳绳次数在110次以上（含110次）的人数分布在第3小组～第6小组，这4个小组的频率之和为0.93，即估计该校初三毕业生一分钟跳绳的达标率约为93%.

【点评】分布表中，各小组的频数与频率的关系都一样，即频数÷频率=样本容量.

（作者单位：江苏省兴化市戴泽初级中学）