基于奇异值分解法的红外热图像序列处理

邢晓军，左宪章



基于奇异值分解法的红外热图像序列处理

邢晓军1,2，左宪章1

（1. 军械工程学院 无人机工程系，河北 石家庄 050003；2.中国人民解放军63810部队，海南 文昌 571300）

针对脉冲涡流热成像检测技术中原始红外图像信噪比较低、温度对比性较差以及存在邻近效应和不均匀加热的问题，将奇异值分解法应用到热图序列的处理中以增强重构图像中的缺陷特征。介绍了奇异值分解法的原理，用奇异值分解法对实验中采集到的热图序列进行处理，以信噪比为指标对图像的处理效果进行评定。结果表明奇异值分解法能够抽取红外热图序列反映缺陷信息特征，可消除邻近效应和不均匀加热的影响，提高图像的信噪比。将奇异值分解法与主成分分析法比较，发现前者重构的图像质量高于后者，是处理红外热图序列的又一有效方法。

奇异值分解；红外图像；脉冲涡流；无损检测

0 引言

飞机、铁轨、轮船等设备通常在高温高压、冲击振动、盐碱等比较恶劣的环境下运行，其表面和内部可能会产生坑洞、裂纹、腐蚀等缺陷，因此需要对设备进行检测。

脉冲涡流热成像无损检测技术能够实现运行设备的在线检测，与传统检测方法相比具有检测效率更高、单次检测面积大、非接触并且不受工件表面状态影响的特点，因此应用十分广泛[1]。到目前为止，国内外学者已经在检测机理、激励装置优化以及红外图像处理等方面作了大量研究，该项技术的发展逐渐趋于成熟[2-7]。

利用脉冲涡流感应热成像技术检测工件时，缺陷的存在会影响涡流流动和热量扩散，通过观察某一时刻的红外热图可以识别出缺陷。但通常情况下感应加热是局部非均匀加热，试件表面发射率、线圈提离高度以及邻近效应会对缺陷的识别造成影响。通过对图像序列进行处理可以减少以上因素的干扰。主成分分析法是处理热图序列的经典有效算法，国内外学者对主成分分析法进行了深入研究并将其改进，提高了缺陷区域与非缺陷区的对比度，增强了缺陷的可识别性[8-12]。此外，余弦变换[13]、脉冲相位法[14-15]、独立成分分析[8,10]、因子分析法[16]均是处理图像序列的有效算法。提高热图处理质量和计算速度、减小计算量是图像处理需要解决的问题。主成分分析法是处理图像的一种有效算法。与主成分分析法相似，奇异值分解（Singular Value Decomposition, SVD）法作为一种统计学的方法，通过少数几个变量描述多个因素之间的相互联系。该方法通过分解数据矩阵，将其表示为酉矩阵和对角阵相乘的形式，根据需要选取酉矩阵模态数量对数据进行重构，可以有效提高计算速度。本文将奇异值分解法应用到热图序列的处理中。首先介绍奇异值分解法的基本原理，然后对感应加热不同阶段的热图序列进行分解，以信噪比为指标衡量该方法的有效性；研究冷却时间对热图重构质量的影响；最后将奇异值分解法与主成分分析法的处理结果进行比较。

1 奇异值分解法的基本原理

奇异值分解是数值计算中最重要的工具之一，在数据降维[17]、图像处理[18]和模式识别[19]中应用广泛。其基本原理如下：

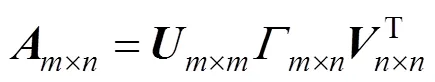
2 对红外图像序列的处理

利用奇异值分解法处理红外热图序列，首先要将热图序列转化为数据矩阵[16]。对试件进行感应加热，用红外热像仪采集红外图像，该图像是随时间变化的温度场信号，温度数据可以转换成图1所示的图像序列，其中，任意一帧图像像素点数据都可构成式(3)所示的二维矩阵，图像序列构成一个三维数据矩阵。图中、分别为每帧图像在列方向和行方向上的像素数，为采集图像的总帧数。

图1 图像序列

对试件进行感应加热，采集到的红外热图序列可构成一个三维矩阵，对该序列进行处理时，首先要将热图序列的三维矩阵转换为二维矩阵。对每帧图像按照图像像素从左到右，从上到下的顺序依次排列，形成一个×行的一维矩阵，如式(4)所示：

F＝[11,12,…,1n, …,x1,…,x]T(4)

热图序列经过转换，可得到个一维矩阵，将这些一维矩阵依次排列可形成一个新的二维矩阵，如式(5)所示：

＝[1,2,…,] (5)

为获得较好的处理效果，在对数据进行奇异值分解前按式(6)、(7)、(8)对数据进行标准化处理：

将热图数据进行标准化处理可去除背景噪声对数据处理的影响。对经标准化处理过的二维矩阵进行奇异值分解，矩阵的每一列表示经验正交函数的一个模态。经验正交函数的第一和第二个模态包含了图像数据80%～90%的变量信息。因此，对数据进行重构时只利用阵的第一列即可反映出缺陷信息。按照式(3)、(4)将图像二维矩阵转化为一维矩阵的方法进行逆向操作，即可把列向量转化为一帧图像，即所求结果。

3 实验设备及检测结果

脉冲涡流热成像无损检测实验系统如图2所示。在45#钢试件上人为加工了浅槽型裂纹。试件长250mm，宽80mm，厚10mm；对宽度为1mm深度为4mm的表面裂纹和宽度为8mm剩余厚度为2mm的下表面裂纹进行检测。感应线圈内通入频率为256kHz的交流电，线圈垂直于裂纹长度方向，对上表面裂纹加热300ms，冷却3s，下表面裂纹加热2s，冷却5s；红外热像仪图像帧频为60Hz，记录试件感应加热过程中的热图序列。

图2 脉冲涡流热成像无损检测实验系统

图3所示为加热300ms后上表面裂纹和加热2s后下表面裂纹附近温度分布的红外图像。该图像由在线式红外检测软件获取，图像中两个三角形状的标志指明了该帧图像中温度最高和最低点的位置，最高温度和最低温度值可以在图中读出。在进行感应加热的过程中，缺陷的存在会阻碍涡流的流动，引起热量的聚集，缺陷部位显示为高温。该试验系统中采用水冷铜管加热，由于试件表面不平或线圈制作工艺有限导致线圈外径并不是水平的，很难保证试件上方线圈提离值一致。除此之外，缺陷尺寸较小时，由于邻近效应的影响，线圈下方非缺陷区域温度也很高，很难将缺陷和邻近效应造成的高温进行区分。

4 实验数据的处理

4.1 奇异值分解处理结果分析

为提高裂纹的识别效率，削弱不均匀加热和邻近效应对缺陷识别的影响，采用奇异值分解法分别对上表面和下表面裂纹感应加热不同阶段的红外热图序列进行处理，并比较处理效果。

图4、图5分别是对上表面和下表面裂纹感应加热不同阶段热图序列进行奇异值分解后的结果。

图4 上表面裂纹热图奇异值分解

图5 下表面裂纹热图奇异值分解

从图中可以看出，经过奇异值分解后，邻近效应得到不同程度的抑制。比较图4(a)、(b)可知，对于上表面裂纹，对冷却阶段热图序列进行奇异值分解比对加热阶段热图序列进行处理效果更好。因为上表面裂纹宽度较小，线圈提离很小且不均匀，对试件表面进行加热时缺陷附近和线圈提离较小的区域温度迅速上升，加热结束后都表现为高温分布。冷却阶段热量扩散时缺陷区热量扩散快，非缺陷区域由于线圈提离不均，试件表面不同区域温度不同，因此经过奇异值分解后线圈下方部分区域高温没有完全消除。对加热和冷却阶段热图序列进行处理，结果如图4(c)所示，缺陷位置表现为高温，图像重构的质量介于(a)与(b)之间。由此可知加热阶段包含较多的噪声，缺陷特征信息更多地体现在冷却阶段。由图5可以看出，对于下表面裂纹，对感应加热不同阶段热图序列进行奇异值分解后缺陷特征都能得到较大的增强。原因是下表面缺陷尺寸较大，剩余厚度较小，加热时缺陷上方温度迅速上升，热扩散时纵向传递的热量到达缺陷位置时发生反射，阻碍了热量的传递，导致缺陷区域比其他区域温度更高。

为了更直观地分析热图处理结果，引入图像信噪比作为量化指标评定处理结果：

定义图像的信噪比：

表1 热图信噪比

由表1可知，无论是上表面还是下表面裂纹，对冷却阶段热图序列进行奇异值分解得到重构图像的信噪比均高于加热阶段。冷却阶段包含较多的缺陷信息，经奇异值分解后可以更好地突出缺陷特征。

4.2 与主成分分析法的比较

将上表面和下表面裂纹感应加热不同阶段热图序列进行主成分分析，图6、图7所示分别为感应加热不同阶段上表面和下表面裂纹的第一、第二主成分。比较图6(a)、(b)可以看出，上表面裂纹冷却阶段热图序列经主成分分析后无法读出缺陷信息，加热阶段热图可以在第二主成分中比较清晰地看出裂纹在长度方向上的延伸；比较图7(a)、(b)可知，下表面裂纹冷却阶段第一主成分包含了较多的热扩散信息，第二主成分图像中沿裂纹长度方向热扩散范围比无缺陷区域上方扩散范围更大，裂纹附近温度更高。加热阶段主成分中也能够看出沿裂纹长度方向热量扩散范围更大，对比度比冷却阶段更高。但比较图6、图7与图4、图5可以看出，主成分分析法对邻近效应和不均匀加热的抑制效果不如奇异值分解法。

图6 上表面裂纹主成分分析

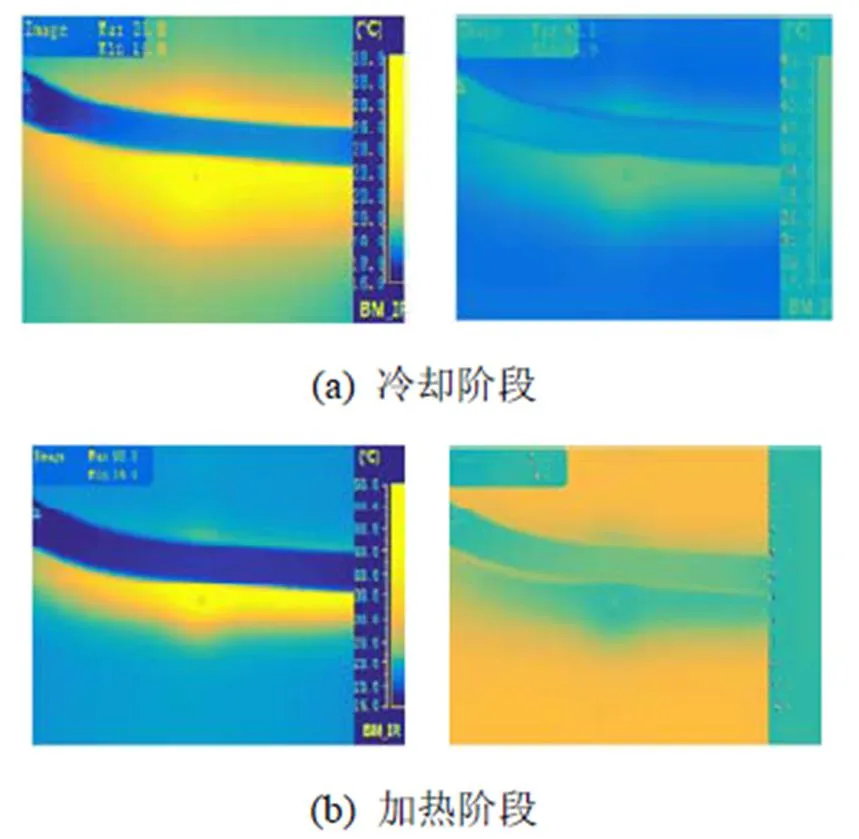
图7 下表面裂纹主成分分析

4.3 对帧数不同的图像序列进行处理

以上分析得知，利用冷却阶段热图序列进行奇异值分解可以削弱邻近效应和不均匀加热的影响，提高缺陷的识别效率。为研究冷却时间对图像序列处理效果的影响，得到最佳处理效果的图像序列的帧数，按照最小帧数为20帧、步长为20帧，逐渐增加处理图像序列的帧数，处理图像帧数越多对应冷却时间越长。处理后图像序列的帧数与信噪比之间的关系如图8所示。可见，随着所处理对象帧数的增加，处理后图像的信噪比不断增大，当达到一定的帧数后，信噪比增速变缓。但随着所处理对象帧数的增加，运算时间也会增加，因此在实际应用中应根据需要选用合适的图像序列帧数。

图8 图像序列帧数与处理后图像信噪比的关系

5 结论

本文利用奇异值分解法对上表面和下表面裂纹感应加热不同阶段的热图序列进行处理，通过分析处理结果可以得到以下结论：

1）用奇异值分解法处理热图时，对冷却阶段热图序列进行处理所得重构图像的信噪比最高，冷却阶段热图序列包含更多的缺陷信息，加热阶段热图序列包含较多噪声。

2）与主成分分析法相比，奇异值分解法能够抑制感应加热过程中不均匀加热和邻近效应的影响，有效增强缺陷的特征。

3）随冷却时间的增加，奇异值分解处理所得图像信噪比先快速增加，冷却达到一定时间后，处理后的图像信噪比增速缓慢。

[1] TIAN G Y, Wilson J, CHENG L, et al. Pulsed eddy current thermography and applications[J]./2011, 96: 205-231.

[2] 常东, 左宪章, 田贵云, 等. 裂纹方向对脉冲涡流热成像的影响[J]. 上海交通大学学报: 自然版, 2013, 47(5): 779-785.

CHANG dong, ZUO Xianzhang, TIAN Guiyun, et al. Analysis of the crack orientation effection on pulsed eddy current stimulated thermography[J].:, 2013, 47(5): 779-785.

[3] Yang S X, TIAN G Y, Abidin I Z, et al. Simulation of edge cracks using pulsed eddy current stimulated thermography[J].,,, 2011, 133: 011008-1-011008-6.

[4] LIU Guofei, LI Guohua. Numerical simulation of defect inspection using electromagnetically stimulated thermography[J].:, 2011, 16(3): 262-265.

[5] Zainal Abidin I, TIAN G Yun, Wilson J, et al. Quantitative evaluation of angular defects by pulsed eddy current thermography[J]., 2010, 43(7): 537-546.

[6] Ramdane B, Trichet D, Belkadi M, et al. 3-D numerical modeling of the thermo-inductive technique using shell elements[J]., 2010, 46(8): 3037-3040.

[7] Tsopelas N, Siakavellas N J. The effect of the angle of inclination of the exciting coil in electromagnetic-thermal non-destructive inspection[J]., 2011, 41(1): 162-177.

[8] BAI L, GAO B, TIAN S, et al. A comparative study of principal component analysis and independent component analysis in eddy current pulsed thermography data processing[J]., 2013, 84(10): 104901-104901-11.

[9] LU X N, HAN J G, HAN S H, et al. Solder bumps inspection using principal component analysis in active thermography[J]., 2014, (912-914): 1529-1533.

[10] BAI Libing, GAO Bin, TIn Shulin, et al. A comparative study of principal component analysis and independent component analysis in eddy current pulsed thermography data processing[J]., 2013, 84(10): 2213-2219.

[11] Omar M A, Parvataneni R, ZHOU Y. A combined approach of self-referencing and principle component thermography for transient, steady, and selective heating scenarios[J]., 2010, 53(5): 358-362

[12] PAN M C, HE Y Z, TIAN G Y, et al. Defect characterization using pulsed eddy current thermography under transmission mode and NDT applications[J]., 2012, 52: 28-36.

[13] Oswald-Tranta B, Sorger M. Localizing surface cracks with inductive thermographical inspection: from measurement to image processing[J]., 2011, 8(2): 149-164.

[14] 胡德洲, 左宪章, 李伟. 基于涡流脉冲相位热成像的金属材料裂纹检测[J]. 应用光学, 2014, 35(4): 656-662.

HU dezhou, ZUO Xianzhang, LI wei. Crack detection for metallic materials based on eddy-current pulsed-phase thermography[J]., 2014, 35(4): 656-662.

[15] HE Y Z., TIAN G Y, PAN M C, et al. Eddy current pulsed phase thermography and feature extraction[J]., 2013, 103(8): 084104-1-084104-4.

[16] 胡德洲, 左宪章, 王建斌, 等. 脉冲涡流热成像缺陷检测图像的因子分析[J]. 红外技术, 2014, 36(12): 1009-1015.

HU dezhou, ZUO Xianzhang, WANG Jianbin, et al. Factor analysis of thermal images for defect detection using pulsed eddy current thermography[J]., 2014, 36(12): 1009-1015.

[17] 李明. 矩阵分解理论在降维中的应用[J]. 吉林师范大学学报: 自然版, 2010, 8(3): 117-120.

LI Ming. The applications of matrix decomposition theory for dimensionality reduction[J].:, 2010, 8(3): 117-120.

[18] 陈勇, 樊强, 张开碧, 等. 利用梯度奇异值分解的图像结构相似度评价[J].半导体光电, 2015, 36(3): 522-526.

CHEN Yong, FAN Qiang, ZHANG Kaibi, et al. Similarity assessment of image structural quality with gradient singular value decomposition[J]., 2015, 36(3): 522-526.

[19] 计雨含, 王晓东, 姚宇. 基于张量奇异值分解的人脸识别方法[J]. 计算机应用, 2015, 35(S1): 117-121.

JI Yuhan, WANG Xiaodong, YAO Yu. Face identification based on tensor singular value decomposition[J]., 2015, 35(S1): 117-121.

Sequence Processing on Thermal Infrared Images Based on Singular Value Decomposition

XING Xiaojun1,2，ZUO Xianzhang1

(1.Department of UAV Engineering, Ordnance Engineering College, Shijiazhuang 050003, China;2. The Chinese People’s Liberation Army 63810, Wenchang 571300, China)

The raw thermal images used in pulsed eddy current thermographic nondestructive testing was characterized with low signal-to-noise ratio(SNR) and temperature contrast. Additionally, there are still uneven heating and proximity effect problems. To avoid the performance degradation caused by these issues, singular value decomposition(SVD) technique was applied in infrared image sequence processing to enhance characteristics of the reconstructed image defects. The SVD was introduced and was used to process infrared images. The image processing effect was evaluated by SNR. The result shows that SVD can extract the algebra characteristics to reflect defect information. It can remove the uneven heating and proximity effects, and increase the SNR of images. Images reconstructed by SVD were compared with those by principal component analysis (PCA). It demonstrated that SVD outperforms PCA in terms of reconstructing images, thus SVD is an effective method to process infrared image sequence.

singular value decomposition，infrared image，pulsed eddy current，non-destructive testing

TG115.28

A

1001-8891(2017)06-0517-05

2016-05-21；

2016-09-20.

邢晓军（1991-），女，山东德州人，硕士研究生，从事电磁热成像无损检测方面的研究。E-mail：xingxiaojun1991@163.com。

河北省自然科学基金（E2014506011）。