基于层次分析法的环境质量评价研究

高晓凤

摘要：指出了随着社会经济的不断发展，好的环境质量不仅可以吸引优秀人才，还能促进城市环境朝更好的方向发展，因此对环境质量的评价显得尤为重要。经过分析建立了以居民经济、居民生活和居民环境为指标的评价体系，采用层次分析法建立判断矩阵求得了各个指标的权重系数，结合各个指标的实际数据和层次分析法所得权重系数可以将各个城市或者地区的环境质量以确定分数的形式表现出来。以天津、河北、山西为例求得了这三个城市的环境质量的综合得分和单指标得分，所得结果符合我国的实际情况，说明了该方法对于环境质量评价的可行性和科学性。

关键词：层次分析法；环境质量评价；矩阵；权重系数；评价体系

1 引言

环境无时无刻不在影响着人们的生活。良好的居住环境不仅可以提高当地人民的身心健康，还能吸引大量的优秀人才，同时这又能反过来促进城市的经济发展和环境质量的改善。但是，在发展经济的同时不可避免会消耗大量资源，并造成一定的环境破坏，这些问题在城市中尤为显著。为了使人们的居住环境不至于进一步恶化，必须在保持经济发展的同时，对环境进行有效的保护。此时，对环境质量的评价就显得尤为重要。

目前系统评价方法有很多种，比较流行的有模糊综合评价法、灰度关联法、层次分析法、主成分分析法、聚类分析法等。针对环境质量综合评价方面的研究，我国一些从事环境质量评价方面的前辈们已经做了大量的工作并取得了一些效果。比如，程兰芳、孙秋萌利用多远统计分析中的聚类分析方法对全国各地的城市环境质量进行了评价[1]；王星火、金永超等人使用主成分分析法对全国主要城市环境质量进行了综合评价[2]；温欣欣、郑育毅等人利用熵权法对福州市的环境综合质量进行了评价[3]。这些方法虽然能够解决一些问题但是也有其局限性，比如有的文章分析相对简单，有的对评价指标之间的相对重要程度没做说明等。层次分析法作为一种比较著名的评价方法在环境质量评价方面的应用少之又少，但是其在绿色制造评价方面研究却十分广泛，比如刘晓晨等人将该方法用于刀具几何角度评价方面取得了很好的效果[4]；王桂萍等人使用该方法对数控机床的绿色度进行评价，也取得了较好的效果[5]。

经过分析并结合前人所做的努力，采用层次分析法对环境质量进行综合的评价，该方法不仅可以解决现有评价方法存在的一些问题还能够以定量方式展示各个城市之间的综合质量得分情况和各子指标得分情况。

2 环境质量综合评价体系的建立

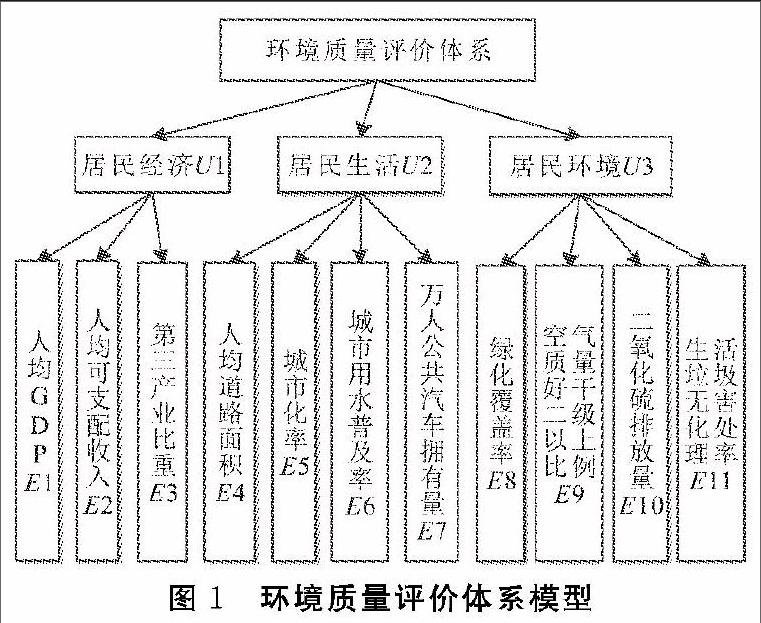
环境质量一般是指一定范围内的环境的整体或者环境的一些主要要素对人类的生存、生活以及发展的适应程度。而环境质量评价是一个基于多层次、多因素、多指标的综合研究过程。传统的环境质量评价往往只将环境污染方面考虑进去，而忽略了人们生活的舒适度，这实际上是不符合实际情况的。比如，一个城市空气环境很好，但是道路交通等都很不方便，那么当地居民对其的环境质量评价打分往往也不会很高。环境质量评价应该包含和人类相关的方方面面，经过对前人研究的总结和分析，将环境质量评价的指标分为以下方面：经济方面、居民生活方面和环境方面。每个指标又可以详细分为更多的子指标，比如环境方面又可以分为城市绿化率、二氧化硫排放量、生活垃圾无害化处理率等。在此研究的环境质量评价体系正是基于这些指标建立的，如图1所示。

3 基于层次分析法的评价体系求解

层次分析法（AHP：Analytic Hierarchy Process）是由美国著名运筹学家T L Saaty教授提出来的一种系统分析方法。这种方法把一个复杂的问题按属性的逻辑关系逐层分解，形成一个层次结构来加以分析，以简化分析问题的难度，并在逐层分解的基础上加以综合，给出复杂问题的求解结果[6]。

3.1 判断矩阵的建立

判断矩阵的建立是层次分析法主要的环节，判断矩阵主要是根据各个指标的相对重要程度而建立起来的。假设层次U所含的子指标有E1，E2，…，En这些指标之间的相对重要程度就构成一个判断矩阵，如表1所示。

3.2 层次单排序

判断矩阵是根据各个指标或者子指标的相对重要程度建立的矩阵，而层次单排序可以理解为对判断矩阵的求解过程，计算出矩阵的最大特征值和其所对应的特征向量，最终定量的表示出每个指标或者子指标相对于上一层的权重系数。比如可以基于人均道路面积、城市化率、城市用水普及率和万人公共汽车拥有量建立判定矩阵，并对该矩阵进行求解，最终所得的权重系数即为相对于居民生活来说的层次单排序。

传统的求解层次单排序的方法有“方根法”和“求和法”两种[10]，这两种方法都是基于手工计算的近似方法，在计算过程中极易出错。事实上随着计算机技术的不断发展人们可以借助一些计算机软件来完成复杂的数学计算，比如，可以使用MATLAB工具中的eig（）函数很快的计算出判断矩阵的最大特征值和所对应的特征向量。最大特征值用来判定判断矩阵的一致性指标，而其对应的特征向量则对应这几种因素的相对重要程度，将特征向量进行归一化处理，即得到该层指标对于上一层指标的层次单排序。层次单排序的具体求解过程如下所示。

假设指标层要素U1， U2，…， Un，根据en/5标度法得到其判断矩阵，利用MATLAB计算出判断矩阵的最大特征值是λmax以及最大特征值对应的特征向量为：

M=[m1，m2，…，mn]T，

那么此指标层的相对权重向量为：

W=[w1，w2，…，wn]T，

W和M满足如下的公式：

wk=mk∑ni=1mi k=1，2，3，…，n。

3.3 一致性检验

虽然学者可以很容易基于指标之间的相对重要程度建立判断矩阵和求解层次单排序，但是判断矩阵的建立是否正确却不得而知，专家在建立判断矩阵时由于人为的因素很可能导致指标之间的重要性不一致，这样的判断矩阵肯定是失效的不能使用的。為了解决这一问题笔者引入一致性检验这一概念，一致性检验是为了确定判断矩阵中各要素的重要性判断是否一致，只有满足一致性检验的判断矩阵才能使用否则就需要重新设置判断矩阵。满足完全一致性的条件是判断矩阵的akj=akl/ajl，但是事实上人们在进行主观判断时对系统评价方案的认识具有片面性，所建立的判断矩阵很难满足完全一致性。此时引入判断矩阵的随机一致性比值来近似检验人们思维判断的一致程度。随机一致性比值记为C.R.，计算公式为[9]：

C.R.=λmax-nR.I.（n-1），n≥3

式中：λmax为判定矩阵的最大特征值；n为判断矩阵的阶数；R.I.为平均一致性指标。

当矩阵是一阶或者是二阶时肯定具有满意的一致性，不用利用上述公式就可判断。对于3阶以上的矩阵只要满足C.R.<0.1，就可以认为该矩阵具有满意的一致性，其中R.I.的值和判断矩阵的阶数有关，具体关系如表3所示。

3.4 层次总排序

层次单排序是对于上一级指标而言的权重系数，而层次总排序是对于目标层的权重系数[11]，层次总排序不需要建立判断矩阵，只需将各个指标层次单排序数据对应上一层的总排序相乘即可。具体求解方法如下。

假设上一层指标U的对应目标层的总排序已经确定，其数值为w；且本层各指标E1，E2，…，En对U的层次单排序结果为w1，w2，…，wn，如果设本层的总排序为

M=[m1，m2，…，mn]T

那么mj满足如下的公式：

mj=w·wj，j=1，2，3，…，n。

3.5 环境质量评价的定量分析

环境质量评价的定量分析可以直观的看到每个城市环境质量评价的综合得分和单指标得分，这样不仅可以使评价结果清楚地展现出来还能给环境评价决策者提供重要的依据。环境质量评价的定量分析具体的求解过程如下。

假设有m个待评价的城市分别为C1，C2，…，Cm，评价指标有n个分别为E1，E2，…，En。则第i个城市对应的第j个指标的数据可用bij来表示，具体指标的数据可查阅相关资料获得。为了防止由于数据单位不同带来的差异需要对数据进行归一化预处理[12]。指标数据经过归一化处理最终组成如下的矩阵。

G=b11b12…b1n

b21b22…b2n

bm1bm2…bmn

注意，由于数据经过了归一化处理故应满足：

∑=1bij=1，j=1，2，…，m，

假设各个指标的层次总排序（总权重）为M=[m1，m2，…，mn]T那么各个城市的综合得分F为：

F=100·G·M=[f1，f2，…，fm]T， （1）

（1）式中f的取值越大说明环境质量越好，需要注意的是如果矩阵G和矩阵M表示的是部分指标数据和与其对应的层次单排序那么得出的结果是城市环境质量评价的单指标得分而不是综合得分。

4 实例分析

经过调查和查阅相关资料获得了某一年度北京、河北、山西三个城市的指标数据，具体见表4。

由此可以得出总权重矩阵：

M=[0.0385，0.1046，0.0574，0.0214，0.0137，0.0582，0.0411，0.0665，0.1809，0.2698，0.1481]T

由（1）式可以得到各个城市环境质量评价的总得分为：

F=100·G·M=[26.33，10.37，9.37]T，

它们分别对应的城市为天津、河北和山西。由数据可知天津市的环境质量评价比河北和山西要好，而山西和河北的环境质量基本相近。

上述得出的结果是环境质量总体的评分情况，在此还可以对其进行单指标的评分，这样可以更科学地分析出城市环境质量之间的差异。以上述数据为例比较这三个城市的居民经济单指标评分。单指标矩阵为：

MU1=[0.1919，0.5217，0.2836]T

城市指标数据只需居民经济所含的三个指标数据即可，

GTU1=

0.56610.22560.2083

0.44290.29060.2665

0.39830.29830.3034

经计算得：

FU1=100·GU1·MU1=[45.37，28.03，26.59]T

它们所对应的城市分别为天津、河北和山西，从单指标评分可以看出天津在居民经济方面要远高于河北和山西，河北在居民经济方面略高于山西。

5 结论

环境质量对居民的生活有很大的影响，好的居住环境不仅可以增加居民的舒适性，反过来也能促进该城市朝更好的方向发展。如何确定城市的环境质量对于人们来说是十分重要的事情，从居民经济、居民生活和环境三个方面建立城市环境质量的评价体系，使用层次分析法对体系进行求解，并结合三个城市的具体指标数据，将三个城市的综合得分和单指标得分以确定数据的方式展示出来。最终经过分析得出天津市的综合得分最高说明其居住环境质量最好，而河北和山西基本相同；就居民经济方面来说天津远高于河北和山西，河北略高于山西。这样的结果与我国城市的实际情况相符合，也说明了该方法对于环境质量评价的可行性和科学性。

参考文献：

[1]程兰芳，孙秋萌. 我国各地城市环境综合评价[J]. 价格月刊，2011，404（3）：88～90.

[2]万星火，金永超，郑俊玲. 基于核主成分分析的环境质量综合评价模型[J]. 电脑知识与技术，2014，10（9）：2125～2127.

[3]温欣欣，郑育毅，张江山. 基于熵权物元可拓模型的福州市环境综合质量评价[J]. 安全与环境工程，2011，18（1）：29～32，52.

[4]劉晓晨，汪永超，李 磊，等. 面向绿色制造的刀具几何角度的优化选择[J]. 组合机床与自动化加工技术，2016（1）：1～3，9.

[5]王桂萍，贾亚洲，周广文.基于模糊可拓层次分析法的数控机床绿色度评价方法及应用[J].机械工程学报，2010，46（3）：141～147.

[6] 谢家平.绿色设计评价与优化[M].武汉：中国地质大学出版社，2004.

[7]駱正清，杨善林.层次分析法中几种标度的比较[J].系统工程理论与实践，2004，24（9）：51～60.

[8]孙东升，朱 懿，周水兴.基于指数标度的层次分析法在桥梁评定中的应用[J].重庆交通大学学报（自然科学版），2010，29（6）：867～870.

[9]Metin D，Serkan Y，Nevzat K.Weapon selection using the AHP and TOPSIS methods under fuzzy environment[J].Expert Systems with Applications，2009，36（13）：8143～8151.

[10]胡天觉，陈维平，曾光明，等. 运用层次分析法对株洲霞湾污水处理厂污水处理工艺方案择优[J]. 环境工程，2000（1）：61～63.

[11]邓仁健，任伯帜，周赛军. 采用三角模糊数层次分析法选择小型污水处理工艺[J]. 环境工程，2010（1）：91～93，111.

[12]Anon.Application of an analytic hierarchy process to hydrocarbon accumulation coefficient estimation[J]. Petroleum Science，2010（3）：337～346.

Research on Environmental Quality Assessment

Based on Analytic Hierarchy Process

Gao Xiaofeng

（College of Architecture and Environment，Sichuan University，Chengdu，Sichuan 610065，China）

Abstract： With the continuous development of social economy，peoples living standards continue to improve，and the environment we live in is changing every moment.Good environment quality can not only attract talented people，but also can promote the development of urban environment towards a better direction.So it is particularlyimportant to the evaluation of environmental quality.Through economic analysis based on residents economy， living and environment as the index evaluation system，using the analytic hierarchy process to establish judgment matrix from which we obtained the weight coefficient of each target，combining the actual data of each index and the analytic hierarchy process （ahp） of the weight coefficient of each city or region can be expressed in the form of environmental quality to determine the score.Finally，in Tianjin， Hebei，Shanxi as examples，we calculated the three citys environmental quality comprehensive scores and single index score.The obtained results conformed to the actual situation in our country，illustrated the feasibility of this method forfeasibility and scientificity of environmental quality assessment.

Key words： analytic hierarchy process； environmental quality assessment； matrix； weight coefficient；assessment system